降低综合题难度为的方法

2023-11-21 理论教育版权反馈

【摘要】：，n），得若令a＝2，n＝3，则可降低命题难度为：1.3 用加边法，因xi≠0（i＝1，2，…＝2n－1D1＋2n－1＋…＋xan－1＋an＝a0xn＋a1xn－1＋a2xn－2＋…

以行列式的形式给出函数后，可与高等数学知识结合命制综合题.

见例1.15.

（A）y＋2＝0 （B）x－4＝0

（C）2y＋40x－7＝0 （D）2y－40x＋7＝0

【解】应选（A）.

故f（x）＝0有三个根x1＝－2，x2＝1，x3＝4.

在［－2，1］上对f（x）应用罗尔定理，有f′（ξ1）＝0，－2＜ξ1＜1；

在［1，4］上对f（x）应用罗尔定理，有f′（ξ2）＝0，1＜ξ2＜4；

在［ξ1，ξ2］上对f′（x）应用罗尔定理，有f″（ξ）＝0，ξ∈（ξ1，ξ2）⊂（－2，4）.

从而f′（x）在x＝ξ处的切线水平，因此切线平行于直线y＝－2.故选（A）.

但是要注意，本题f″（x）＝6x－6，当x∈（－2，4）时，f″（x）∈（－18，18），即当直线y＝ax＋b的斜率a∈（－18，18）时，均可能平行于某切线，所以选项（B），（C），（D）设置为，均不符合题意.

1.1 计算行列式： pagenumber_ebook=22,pagenumber_book=14

1.2 计算n＋1阶行列式：

1.3 计算n阶行列式：

其中xi≠0，i＝1，2，…，n.

1.4 计算行列式：

1.5 计算行列式：

1.6 解方程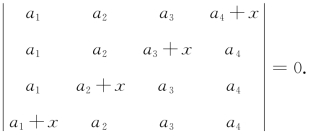 pagenumber_ebook=23,pagenumber_book=15

1.7 n阶行列式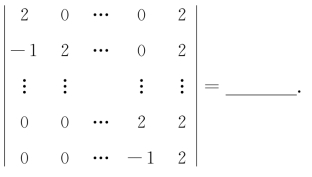 pagenumber_ebook=23,pagenumber_book=15

1.8 计算行列式：

1.9 设

则多项式f（x）可能的最高次数是（）.

（A）1 （B）2 （C）3 （D）4

1.10 设α1，α2，α3 均为3维列向量，记矩阵

A＝［α1，α2，α3］，B＝［α1＋α2＋α3，α1＋2α2＋4α3，α1＋3α2＋9α3］.

如果|A|＝1，那么|B|＝________.

1.1 【解】

【注】本题的行列式是“爪形行列式”（只有第1列、第1行及主对角线元素不为零，其余元素均为零的行列式），这种行列式都可以化为“基本形”行列式.

1.2 【分析】观察每行元素发现，第i行和第i＋1行（i＝1，2，…，n）有n个对应元素成a 倍.

【解】将第i＋1行乘（－a）加到第i行（i＝1，2，…，n），得

【注】若令a＝2，n＝3，则可降低命题难度为：

1.3 【解】用加边法，

因xi≠0（i＝1，2，…，n），故(www.chuimin.cn)

1.4 【解】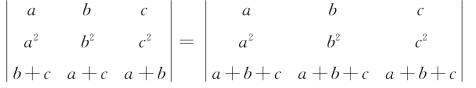 pagenumber_ebook=25,pagenumber_book=17

1.5 【解】观察元素之间的规律，知将第1行乘（－1）加到第2行，再将得到的新行列式的第2行乘（－1）加到第3行，依此类推，得

由范德蒙德行列式得

1.6 【解】

故方程的根为x＝0，x＝－（a1＋a2＋a3＋a4）.

1.7 【解】应填2n＋1－2.

将此行列式记为Dn，按第1行展开，得Dn＝2·Dn－1＋（－1）1＋n·2（－1）n－1，得到递推公式

Dn＝2Dn－1＋2（n＞1）.

于是

Dn＝2Dn－1＋2＝2（2Dn－2＋2）＋2＝22Dn－2＋22＋2＝…

＝2n－1D1＋2n－1＋…＋22＋2＝2n＋2n－1＋…＋22＋2，

Dn＝2n＋1－2.

1.8 【解】按行列式Dn＋1 的最后1列展开，得

Dn＋1＝x·（－1）（n＋1）＋（n＋1）Dn＋an·（－1）1＋（n＋1）·（－1）n＝xDn＋an，

其中行列式Dn 是与行列式Dn＋1 结构相同的n阶行列式.由此，得到递推公式Dn＋1＝xDn＋an.于是，逐次递推得到

Dn＋1＝x（xDn－1＋an－1）＋an

＝x2Dn－1＋xan－1＋an

＝x2（xDn－2＋an－2）＋xan－1＋an

＝x3Dn－2＋x2an－2＋xan－1＋an

＝…

＝xnD1＋xn－1a1＋xn－2a2＋…＋xan－1＋an

＝a0xn＋a1xn－1＋a2xn－2＋…＋an－1x＋an，

其中D1＝a0.

1.9 【解】应选（A）.

当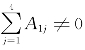 pagenumber_ebook=27,pagenumber_book=19 时，f（x）是关于x的一次多项式；当时，f（x）是常数，故多项式f（x）可能的最高次数是1，应选（A）.

【注】有的读者凭直觉选择（D），显然是错误的.

1.10 【解】应填2.

方法一利用行列式的性质计算.

方法二利用矩阵的性质计算.

【注】方法二中用到了范德蒙德行列式.

降低综合题难度为的方法

相关推荐