首页理论教育线性代数9讲：A相似于B，求B的方法

线性代数9讲：A相似于B，求B的方法

2023-11-21 理论教育版权反馈

【摘要】：（与第7讲、第8讲综合，考生需学习相关知识后再研读此点）（1）见例1.13，例1.14.（2）若A相似于B，则例1.9设A＝［α1，α2，α3］是3阶矩阵，且|A|＝5，若B＝［α1－3α2＋2α3，α2－2α3，2α2＋α3］，则|B|＝________.【解】应填25.方法一利用行列式的性质.|B|＝|α1－3α2＋2α3，α2－2α3，5α3|＝5|α1－3α2＋2α3，α2－2α3，α3

（与第7讲、第8讲综合，考生需学习相关知识后再研读此点）

（1）见例1.13，例1.14.

（2）若A相似于B，则

例1.9设A＝［α1，α2，α3］是3阶矩阵，且|A|＝5，若

B＝［α1－3α2＋2α3，α2－2α3，2α2＋α3］，

则|B|＝________.

【解】应填25.

方法一利用行列式的性质.

|B|＝|α1－3α2＋2α3，α2－2α3，5α3|

＝5|α1－3α2＋2α3，α2－2α3，α3|

＝5|α1－3α2，α2，α3|

＝5|α1，α2，α3|＝5|A|

＝5×5＝25.

方法二 B＝［α1－3α2＋2α3，α2－2α3，2α2＋α3］＝［α1，α2，α3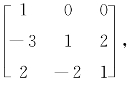］ pagenumber_ebook=20,pagenumber_book=12

故

例1.10 已知n阶行列式|A|＝3，将|A|中的每一列减去其余各列得到的行列式记为|B|，则|B|＝________.

【解】应填3（2－n）2n－1.(www.chuimin.cn)

将A按列分块，记A＝［α1，α2，…，αn］，则有

例1.11 设A是n阶矩阵，满足AAT＝E，其中E是n阶单位矩阵，AT是A的转置矩阵，则＝________.

【解】应填0.

由AAT＝E，得

故

又，于是

例1.12 设A是n 阶矩阵，|A|＝1，则|（2A）*|＝________.

【解】应填2n2－n.

由第3讲中“二”的“1（2）”的公式，知（2A）*＝2n－1A*，A*＝|A|A－1＝A－1，于是

例1.13 设3阶矩阵A有特征值－1，2，3，A*是A的伴随矩阵，则|A＋2A*|＝________.

【解】应填44.

|A|＝（－1）×2×3＝－6.A*的特征值为，即6，－3，－2，则2A*的特征值为12，－6，－4，A＋2A*的特征值为11，－4，－1，故|A＋2A*|＝11×（－4）×（－1）＝44.

例1.14 设A是4阶矩阵，A*是A的伴随矩阵，A*的特征值为1，－1，－2，4，则|A3＋2A2－A－3E|＝________.

【解】应填

|A*|＝1×（－1）×（－2）×4＝8≠0，A*可逆，于是A可逆.又，得|A|＝2.故A的特征值，即为

设f（A）＝A3＋2A2－A－3E，则f（A）的特征值为