首页理论教育数学归纳法的低阶到高阶应用

数学归纳法的低阶到高阶应用

2023-11-21 理论教育版权反馈

【摘要】：，n－1，n）供考生参考：事实上，选第1列展开是基于Dn 的这种元素分布规律，若选第n列展开，余子式便不是Dn－1，破坏了元素分布规律，无法建立递推公式.例1.7 证明范德蒙德行列式其中用第一数学归纳法证明.当n＝2时，有命题成立.设当n＝k（≥3）时，k阶范德蒙德行列式命题成立，则当n＝k＋1时，对于Dk＋1，依次将第k行乘（－x1）加到第k＋1行，将第k－1行乘（－x1）加到第k行，…

涉及n阶行列式的证明型计算问题，可考虑数学归纳法.

第一数学归纳法：第二数学归纳法：

①验证n＝1时，命题成立；①验证n＝1和n＝2时，命题成立；

②假设n＝k时，命题成立；②假设n＜k时，命题成立；

③证明n＝k＋1时，命题成立.③证明n＝k时，命题成立.

则命题对任意正整数n成立.则命题对任意正整数n成立.

见例1.7.见例1.8.

例1.1 设A为10×10矩阵 pagenumber_ebook=14,pagenumber_book=6 ，计算行列式|A－λE|，其中E为10阶单位矩阵，λ为常数.

【注】（*）处来自 pagenumber_ebook=14,pagenumber_book=6

例1.2 行列式 pagenumber_ebook=15,pagenumber_book=7

【解】应填x4.

先将所求行列式的第1行的（－1）倍分别加到第2，3，4行上，得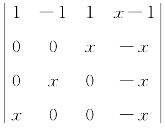 pagenumber_ebook=15,pagenumber_book=7 ，再将所得行列式的第1列、第2列和第3列依次加到第4列上，得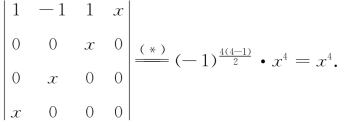

【注】（*）处来自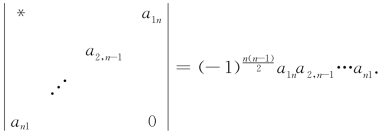 pagenumber_ebook=15,pagenumber_book=7

例1.3 设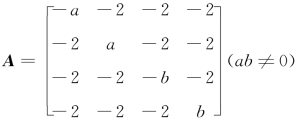 pagenumber_ebook=15,pagenumber_book=7 ，E为4阶单位矩阵，则|2E－A|＝________.

【解】应填a2b2.

【注】（*）处来自 pagenumber_ebook=15,pagenumber_book=7

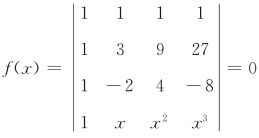例1.4 求 pagenumber_ebook=16,pagenumber_book=8 的所有根.

故f（x）＝0的所有根为1，3，－2.

【注】（*）处来自范德蒙德行列式.

例1.5 计算n阶行列式：

【解】

将第1行乘（－xi）加到第i＋1行（i＝1，2，…，n），再将第i列乘xi－1（i＝2，3，…，n＋1）加到第1列，得

【注】（*）处来自加边法.

例1.6 计算n阶行列式：

【解】按第1列展开，得

下面做递推，得

Dn＝bDn－1＋an＝b（bDn－2＋an－1）＋an＝b2Dn－2＋an－1b＋an(www.chuimin.cn)

＝b2（bDn－3＋an－2）＋an－1b＋an

＝…＝bn－1D1＋a2bn－2＋…＋an－1b＋an，

其中

【注】（*）处提醒考生注意，Dn 的元素分布规律应从右下角往左上看，写出Dk（k＝1，2，…，n－1，n）供考生参考：

事实上，选第1列展开是基于Dn 的这种元素分布规律，若选第n列展开，余子式便不是Dn－1，破坏了元素分布规律，无法建立递推公式.

例1.7 证明范德蒙德行列式

其中

【证】用第一数学归纳法证明.当n＝2时，有

命题成立.设当n＝k（≥3）时，k阶范德蒙德行列式命题成立，则当n＝k＋1时，对于Dk＋1，依次将第k行乘（－x1）加到第k＋1行，将第k－1行乘（－x1）加到第k行，…，将第1行乘（－x1）加到第2行，得

按第1列展开，得

按列提出公因式（xi－x1），得

等式右边的行列式为k阶范德蒙德行列式，由归纳法假设，它等于，于是

故对正整数n≥2命题成立.

例1.8 证明：n阶行列式

【证】用第二数学归纳法证明.

当n＝1时，D1＝2a＝（1＋1）a1，命题成立.

当n＝2时， pagenumber_ebook=18,pagenumber_book=10 ，命题成立.

假设n＜k时，命题成立，当n＝k（≥3）时，Dk 按第1列展开，得

得证，命题成立.

【注】本题亦可用递推法，由上述解答得递推关系

Dn＝2aDn－1－a2Dn－2，Dn－aDn－1＝aDn－1－a2Dn－2＝a（Dn－1－aDn－2），

递推得

Dn－aDn－1＝a（Dn－1－aDn－2）＝a2（Dn－2－aDn－3）＝…＝an－2（D2－aD1），

其中D1＝2a，D2＝3a2，代入得Dn－aDn－1＝an－2·a2＝an，则

Dn＝aDn－1＋an＝a（aDn－2＋an－1）＋an＝a2Dn－2＋2an＝…

＝an－1D1＋（n－1）an＝2an＋（n－1）an＝（n＋1）an.