学习二进制整数运算-实用指南

2023-11-21 理论教育版权反馈

【摘要】：任务描述二进制整数运算有自己的运算法则,与十进制整数运算比较起来相对简单。任务解析本任务要求掌握二进制整数的加减法及逻辑“与”运算,特别是逻辑“与”运算在计算机网络的学习中非常有用。意思是无论0、1,与0相“与”,结果为0;与1相“与”,则结果为原运算数。

任务描述

二进制整数运算有自己的运算法则,与十进制整数运算比较起来相对简单。

本任务将详细介绍二进制整数的加减法运算和逻辑“与”运算。

任务解析

本任务要求掌握二进制整数的加减法及逻辑“与”运算,特别是逻辑“与”运算在计算机网络的学习中非常有用。

回忆一下二进制的特点:逢二进一,这里说的是二进制的进位规则,那么二进制的借位规则呢,和十进制相仿,是“借一当二”。

二进制加法法则如下:

0＋0＝0 0＋1＝1 1＋0＝1 1＋1＝10（向高位进位）

二进制减法法则如下:

0-0＝0 1-0＝1 1-1＝0 0-1＝1（向高位借位）

二进制逻辑“与”法则如下（逻辑“与”运算符通常用“∧”表示）:

0∧0＝0 0∧1＝0 1∧0＝0 1∧1＝1

二进制逻辑“与”法则也可用文字描述:全1为1,否则为0。意思是两个运算数如果全为1,则运算结果为1;其余情况下运算结果都为0。

任务实施

一、二进制整数的加法运算

例1:试计算（1001）2＋（1100）2,采用竖式计算的过程如图1-5所示。

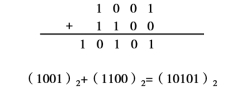
pagenumber_ebook=19,pagenumber_book=12

图1-5

注意:本例中在最高位运算时有进位。

二、二进制整数的减法运算(www.chuimin.cn)

例2:试计算（10101）2-（1100）2,采用竖式计算的过程如图1-6所示。

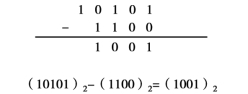
pagenumber_ebook=19,pagenumber_book=12

图1-6

注意:本例中被减数次高位运算时有借位。

三、二进制整数的逻辑“与”运算

例3:试计算（1001）2∧（1100）2,采用竖式计算的过程如图1-7所示。

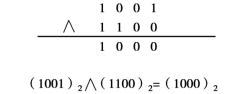
pagenumber_ebook=19,pagenumber_book=12

图1-7

任务小结

本任务中二进制整数的加减法运算,请仿照十进制数的运算进行。逻辑“与”运算初次接触,请牢记其运算法则并多加练习。

拓展提高

还记得在任务3中,请大家记忆的一些常用的十六进制数吗？学习二进制运算后,可以将一些特殊的十进制整数很快地转换成二进制整数,比如248、240、224等。

可以这样转换:248＝255-7＝（11111111）2-（111）2＝（11111000）2,为什么会将248转换成255-7,想一下,请试着转换240和224。

二进制逻辑“与”法则还有一种文字描述:与0清零,与1保留。意思是无论0、1,与0相“与”,结果为0;与1相“与”,则结果为原运算数。笔者比较喜欢按这一种运算法则来进行运算。

课后自测

1.完成至少5组二进制整数的加法运算。

2.完成至少5组二进制整数的减法运算。

3.完成至少5组二进制整数的逻辑“与”运算。