完美实现十进制整数与二进制整数的转换

2023-11-21 理论教育版权反馈

【摘要】：任务描述十进制在日常生活中使用较为广泛,而所有信息在计算机中都是以二进制的形式存储,因此这两种进制数之间的转化显得尤为重要。任务解析本任务着重要求掌握十进制整数与二进制整数之间的转换方法,请记住:十进制整数转二进制整数采用除2取余法;二进制整数转十进制整数采用按权展开求和法。

任务描述

十进制在日常生活中使用较为广泛,而所有信息在计算机中都是以二进制的形式存储,因此这两种进制数之间的转化显得尤为重要。

本任务将详细介绍十进制整数与二进制整数之间的转换方法。

任务解析

本任务着重要求掌握十进制整数与二进制整数之间的转换方法,请记住:十进制整数转二进制整数采用除2取余法;二进制整数转十进制整数采用按权展开求和法。

任务实施

一、十进制整数转二进制整数

十进制整数转换成二进制整数,就是一个连续除以2的过程,即将要转换的十进制整数除以2,得到商和余数,再将商作为被除数继续除以2,也得到商和余数,以此类推,直到商为0为止,最后将所有余数倒序排列,所得到的数就是转换之后的二进制整数,故此方法称为除2取余法。

例1:将十进制数13转化为二进制数的过程如图1-1所示。

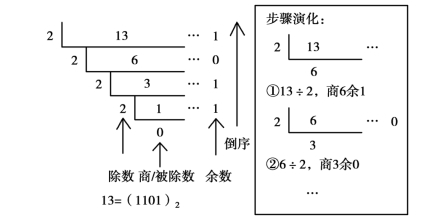
pagenumber_ebook=12,pagenumber_book=5

图1-1

注意:转换过程中所得的余数一定要倒序排列才能得到正确的转换结果!

二、二进制整数转十进制整数

在任务1中学习了按权展开式,实际上,二进制整数转换成十进制整数的方法就是将二进制整数写成按权展开式,然后按十进制计算其和即可。(www.chuimin.cn)

例2:将（1001）2转换成十进制的过程如下。

（1001）2＝1×23＋0×22＋0×21＋1×20＝8＋1＝9

任务小结

本任务较为简单,但也有一个容易犯错的地方,那就是在除2取余法中,经常有人忘记余数需要进行倒序排列,才能得到最终正确的结果。

拓展提高

请务必记住15以内的二进制整数,请至少记住8位二进制整数中每位上的权值,这样在进行二进制整数和十进制整数转换时速度会更快。

例如:（10001111）2＝143,笔者会直接用128加上15,因为最高位上的1,它的权值为27,也就是128,低位上的（1111）2。

又例如:97＝（1100001）2,笔者是这样计算的,97＝64＋32＋1,64是第6位上的权值（26）,32是第5位上的权值（25）,1是第0位上的权值（20）,所以只需要在二进制整数的相应位上置1即得到结果。

课后自测

1.填写下表并熟记。

pagenumber_ebook=13,pagenumber_book=6

2.完成至少10组十进制整数与二进制整数之间的相互转换。