流向桥墩的水流受到桥墩阻挡，桥墩周围的水流结构发生急剧变化，水流的绕流使流线严重弯曲，床面附近形成螺旋形水流，剧烈淘刷桥墩周围，特别是迎水面的河床泥沙，形成冲刷坑的现象，称为局部冲刷。图6-16桥墩局部冲刷水流结构示意图图6-17桥墩局部冲刷示意图图6-18hb—v曲线根据模型试验和观测资料可知，桥墩局部冲刷深度hb与涌向桥墩的流速v有关。这时冲刷坑外缘与桥墩前端坑底的最大高差，就是最大局部冲刷深度hb。......
2023-11-20
简单直线相关桥涵水文学成果
【摘要】：如果点子分布的平均趋势接近直线，则可考虑用图解法或计算法进行直线相关分析。根据确定的相关线或相关方程就可由x系列插补展延y系列。图3-19简单直线相关2.相关计算法基于最小二乘法的线性回归模型。将式、式代入式y=a+bx得式称为y倚x的回归方程式，它的图形称为y倚x的回归线或相关线。使用回归线时，对此必须给予注意。
设xi、yi代表两同步实测系列，计有n对，以自变量xi为横坐标值，以倚变量yi为纵坐标值，将相关点（xi，yi）绘在方格纸上，根据点子分布情况判断是否属直线相关。如果点子分布的平均趋势接近直线，则可考虑用图解法或计算法进行直线相关分析。
1.相关图解法
如果相关点分布集中，可以直接利用作图法求相关线及其相关方程。相关线可根据点群分布趋势，通过点群中心目估定出（图3-19），它反映了两变量间的平均关系。
在目估定线时应注意以下几点：应使相关线两侧点据的离差∑（+Δy）与∑（-Δy）大致相等；对离差较大的个别点不得轻率地改动或删略，经查明原因，如果没有错误或不合理处，定线时还要适当照顾，但不宜过分迁就，要全盘考虑相关点的总趋势；相关线应通过同步系列的均值点
，这可由下面计算法得到证明。
设相关直线的方程为
式中 a、b——方程待定参数，可由图上直接求得，即a为直线在纵轴的截距，b为直线的斜率。
根据确定的相关线或相关方程就可由x系列插补展延y系列。该法简便实用，一般精度尚可，但目估定线有一定的任意性，且缺乏一个定量指标来判断两个变量间关系的密切程度。
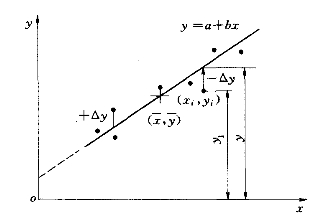
图3-19 简单直线相关
2.相关计算法
（1）基于最小二乘法的线性回归模型。如果相关点的分布较分散，目估定线没有把握，或当精度要求较高时，则最好采用相关计算法。即根据x、y的同步实测资料，用数学公式来计算确定相关方程（回归方程）及其图形，并计算用来表示相关密切程度的相关系数r。
设相关直线y=a+bx，从图3-19可以看出，相关点（xi，yi）与直线在纵轴方向的离差为Δyi=yi-y=yi-a-bxi，一般我们希望直线与实测点能“最佳”拟合，这就需以离差平方和最小为目标推求待定参数a、b，即
为了使上式取得极小值，只需分别对a、b求一阶偏导数，并使其等于零，即令
解方程组，可得
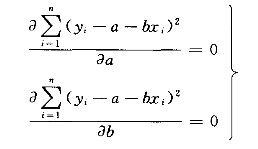
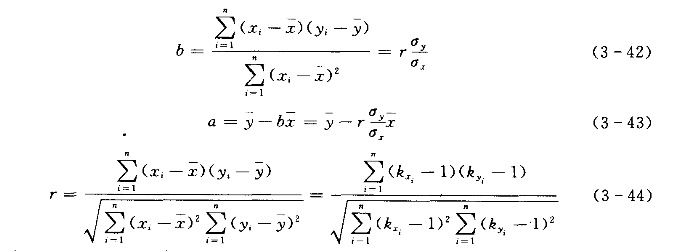
以上式中 F（a，b）——目标函数；
——x、y系列的均值；
σx、σy——x、y系列的均方差；
r——相关系数，表示x、y间关系的密切程度。
将式（3-42）、式（3-43）代入式y=a+bx得
式（3-45）称为y倚x的回归方程式，它的图形称为y倚x的回归线或相关线（图3-20中的1线）。显然，由式（3-45）可见，回归线一定通过两系列的均值点
，回归线的斜率为
，它称作y倚x的回归系数，并记为Ry/x，即
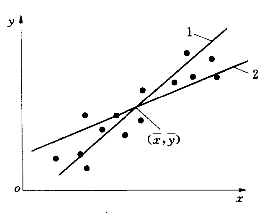
图3-20 回归线
1—y倚x的回归线；2—x倚y的回归线
必须注意，由回归方程所定的回归线只是观测资料平均关系的配合线，观测点不会完全落在此线上，而是分布于两侧，说明回归线只是在一定标准情况下与实测点的最佳配合线。
同理，可推出x倚y的回归方程式（其图形如图3-20中的2线）为
其中
一般y倚x的回归线与x倚y的回归线并不重合，但有一公共交点
。使用时必须辨别清楚，由x求y时，用式（3-45）；由y求x时，用式（3-47）。
（2）基于模糊加权的线性回归模型。基于最小二乘法的线性回归分析计算简便，应用最广。但近代关于数理统计中稳健性的研究发展，用基于残差平方和最小为目标的最小二乘法估计有时很不理想。例如，个别异常点常使回归方程有较大的偏离，致使回归方程欠稳定。于是人们提出了许多其他的目标函数来克服最小二乘法估计存在的这一缺点。本部分内容简要介绍模糊加权的线性回归分析计算，使读者对该法有一个概略的了解，但不作为教学上的要求。
如图3-19所提的相关点（xi，yi）与直线在纵轴方向的离差仍为Δyi=yi-y=yia-bxi，于是可用某个Δyi的函数uM（Δyi）来描述点（xi，yi）对于直线M（称回归直线为M）的隶属程度（隶属度的概念请参阅有关模糊数学书籍），显然uM（Δyi）至少应满足如下两个条件：
（1）当Δyi→0时，uM（Δyi）=1；
（2）当Δyi→±∞时，uM（Δyi）=0。
其实式中的Δyi即是用y去估计yi的残差，它服从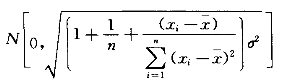
分布，当n较大时，它近似服从N［0，σ］分布，基于上述分析，可给出一种uM（Δyi）的表达式。
设有n组观测数据（xi，yi）（i=1，2，…，n），则某点（xi，yi）对回归线M的隶属度uM（Δyi）为
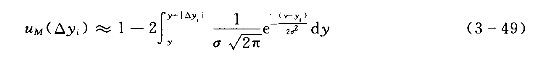
其中均方差σ可用式（3-50）来估计：
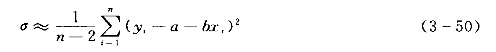
根据隶属度可作为权重的原理，以uM（Δyi）为权重的加权离差平方和最小为目标，即
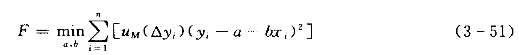
对这类问题可用非线性规划技术求解极值，最终求出待定参数a、b，其他同上。
3.相关分析的误差
（1）回归线的误差。回归线仅是观测点据的最佳配合线，因此回归线只反映两变量间的平均关系，利用回归线来插补延长系列时，总有一定的误差。这种误差有的大，有的小，根据误差理论，其分布一般服从正态分布。为了衡量这种误差的大小，常采用均方误来表示，如用Sy表示y倚x的回归线的均方误，yi为观测点据的纵坐标，
为由xi通过回归线求得的纵坐标，n为观测项数，则
(www.chuimin.cn)
同样，x倚y回归线的均方误Sx为
式（3-52）、式（3-53）皆为无偏估值公式。
回归线的均方误Sy与变量的均方差σy从性质上讲是不同的。前者由观测点与回归线之间的离差求得，而后者由观测点与它的均值之间的离差求得。根据统计学上的推理，可以证明两者具有下列关系：
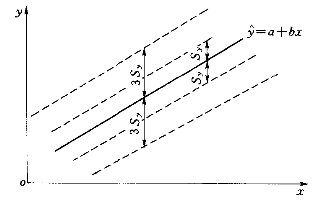
图3-21 y倚x回归线的误差范围
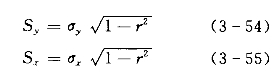
如上所述，由回归方程式算出的
值，仅仅是许多yi的一个“最佳”拟合或平均趋势值。按照误差原理，这些可能的取值yi落在回归线两侧一个均方误范围内的概率为68.27%，落在3个均方误范围内的概率为99.7%，如图3-21所示。
必须指出，在讨论上述误差时，没有考虑样本的抽样误差。事实上，只要用样本资料来估计回归方程中的参数，抽样误差就必然存在。可以证明，这种抽样误差在回归线的中段较小，而在上下段较大。使用回归线时，对此必须给予注意。
（2）相关系数及其误差。式（3-54）和式（3-55）给出了S与σ、r的关系。令y倚x时的相关系数记为ry/x，x倚y时的相关系数记为rx/y，则有
相关系数的两种情况是相等的，即
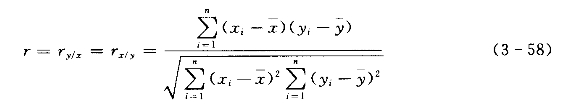
且
相关程度密切与否，一般用r2的大小来判定，称r2为相关平方系数。由式（3-54）和式（3-55）可知：
1）若r2=1，则均方误Sy（或Sx）=0，表示对应值xi、yi均落于回归线上，两变量间具有函数关系，亦即前面说的完全相关。
2）若r2=0，则Sy=σy或Sx=σx，此时误差值达到最大值，说明以直线代表点据的误差达到最大，这两种变量没有关系，亦即前面说的零相关，也可能是非直线相关。
3）若0＜r2＜1，介于上述两种情况之间时，其相关程度密切与否，视r的大小而定。r值越大，均方误Sy（或Sx）越小。当r愈接近于1，点据愈靠近于回归直线，x、y间的关系愈密切。r为正值时，表示正相关；r为负值时，表示负相关。
必须指出，相关系数r不是从物理成因关系导出的，而是从直线拟合点据的误差概念推导出来的，因此当r=0（或接近于零）时，只表示两变量间无直线关系存在，但仍可能存在非直线关系，此时应根据相关图点据的趋势另拟回归曲线。
在相关分析计算中，相关系数是根据有限的实际资料（样本）计算出来的，必然会有抽样误差，一般通过相关系数的均方误来判断样本相关系数的可靠性，按统计原理，相关系数的均方误为
【例3-7】 已知某地区甲、乙两站具有1965年及1967～1983年计18年的年雨量同步资料，如表3-10中（1）～（4）栏所列，试用相关计算法进行甲、乙两站年雨量相关分析；又已知1966年甲站年雨量为945.7mm，试插补该年乙站缺测的年雨量。
解：因甲、乙两站属同一地区，气候条件较一致，从物理成因上分析，两站年雨量间是有联系的，因此，可进行相关计算。设甲站年雨量x为自变量，乙站年雨量y为倚变量，按下列步骤进行计算。
（1）将xi与yi的对应值点绘于方格纸上得各相关点，如图3-22所示。由图可见，点群分布趋势呈直线，故可作y倚x的直线回归计算。
（2）计算x、y系列的均值：
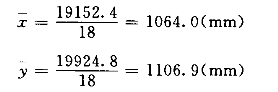
（3）计算表3-10中（5）～（11）栏的各项数值。
（4）计算Cvx、Cvy及σx、σy：
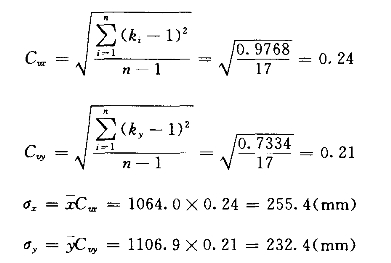
表3-10 甲站与乙站年雨量相关计算表
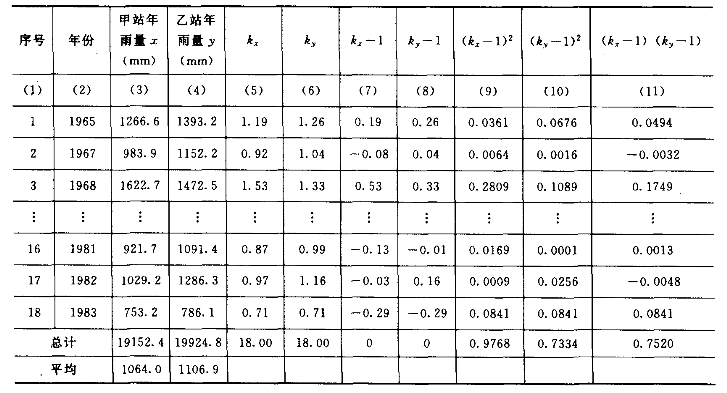
（5）计算相关系数r：
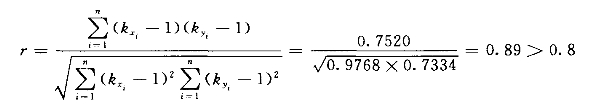
可见甲、乙两站年雨量相关较密切。
（6）计算回归系数Ry/x：
（7）由式（3-45）求得y倚x的回归方程式为：
y-1106.9=0.81（x-1064.0）
或
y=0.81x+245.1
由方程确定的回归线如图3-22所示。
（8）计算回归直线的均方误：
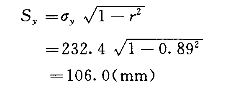
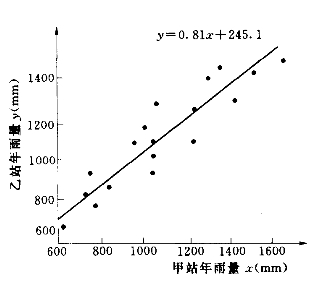
图3-22 甲站与乙站年雨量相关图
（9）由回归方程求得1966年乙站年雨量：
y=0.81×945.7+245.1=1011.1（mm）
有关桥涵水文学的文章
- 详细阅读
-
小桥涵布设原则-桥涵水文学成果详细阅读
应根据沿线地形、地质、水文等条件，结合全线排水系统，适应农田排灌，经济合理地布设小桥涵，达到规范规定设计洪水频率的排水能力。两冲积扇间洼地，亦应布设小桥涵。在漫流无明显沟槽地带，宜采取分片泄洪，在主要水流处布设小桥涵，但不宜过分集中布设。排灌渠上小桥涵的孔径，可按排灌渠的设计过水断面拟定。寒冷地区的小桥涵孔径及高度应考虑涎流冰的影响。......
2023-11-20
-
学习如何绘制简单直线详细阅读
根据相关直线或相关方程就可由x插补延长系列y。按照这一准则确定的相关直线称最小二乘法准则，由此求得的相关方程称为y倚x的回归方程，相应相关直线也称为回归线。将式、式代入式得y倚x的回归方程——x、y系列的模比系数；r——相关系数，表示x、y之间线性相关的密切程度。数理统计中经过研究，由式估计回归方程的误差称δy为y倚x回归线的均方误，式中各符号含义同前。......
2023-06-21
- 详细阅读
- 详细阅读
-
桥涵水流图示-桥涵水文学详细阅读
根据涵洞出水口是否被下游水面淹没，可分为自由式出流与淹没式出流两类。图8-10无压力式涵洞水流图式图8-11半压力式涵洞水流图式当工程上采用半压力式涵洞时，涵底纵坡常用i≥ik。......
2023-11-20
-
桥涵水文学：经验频率曲线揭示成果详细阅读
然后，徒手目估通过点群中心连成一条光滑曲线，即得水文变量x的经验频率曲线。但多数站实测水文资料年限较短，经验频率曲线往往不能满足设计的要求。例如，n=30年，系列中最大值的经验频率P为3.2%，当设计上需要推求稀遇频率的设计值xP时，就必须将经验频率曲线进行外延。图3-10某站年雨量经验频率曲线......
2023-11-20
-
桥涵水文学：恒定流连续方程的成果详细阅读
连续方程是个不涉及任何作用力的运动学方程，所以，它无论对于理想（非粘性）液体或实际（粘性）液体都适用。图1-7元流束图1-8沿程有流量流进示意图连续方程不仅适用于恒定流条件下，而且在边界固定的水流中，即使是非恒定流，对于同一时刻的两过水断面仍然适用。上述总流的连续方程是在流量沿程不变的条件下得出的。图1-9例1-1图解：根据连续方程可得：......
2023-11-20
相关推荐