当使用流速仪测流有困难时，使用浮标测流是切实可行的办法。用水面浮标法测流时，应先测绘出测流断面上水面浮标速度分布图。断面虚流量乘以浮标系数，即得断面流量。在上游浮标投放断面沿断面均匀投放浮标，投放的浮标数目大致与流速仪测流时的测速垂线数目相当。从水面虚流速分布图上内插出相应各测深垂线处的水面虚流速；再按式～式，求得断面虚流量Qf乘以浮标系数Kf，即得断面流量Q。......
2025-09-30
桥涵水文学：目估适线法成果
【摘要】：下面以求矩适线法、三点适线法及权函数法为例详细说明目估适线法的具体过程。利用本章第4节的公式计算和Cv值，并假定Cs值，作为三个统计参数的初始值，通过适线来确定统计参数值的方法，就称为求矩适线法。按公式推算所求洪水频率的流量：Q2%=×1839=4119Q1%=×1839=4561Q0.33%=×1839=5241表3-6流量频率计算表续表表3-7频率曲线选配计算表三点适线法。 利用［例3-4］的年最大流量资料，用三点适线法确定其统计参数、Cv和Cs。
目估适线法估计频率曲线参数的具体步骤如下：
（1）将实测资料由大到小排列，计算各项的经验频率，在几率格纸（几率格纸的纵坐标等分，而横坐标不等分，几率格纸的横坐标分格见附表5）上点绘经验点据（纵坐标为变量的取值，横坐标为对应的经验频率）。
（2）选定水文频率分布线型（一般选用皮尔逊Ⅲ型）。
（3）假定一组参数
、Cv和Cs。为了使假定值大致接近实际，可用矩法、三点法或权函数法求出三个参数的值，作为第一次的
、Cv和Cs的假定值。当用矩法估计时，因Cs的抽样误差太大，一般不计算Cs，而是根据经验假定Cs为Cv的某一倍数。
（4）根据假定的
、Cv和Cs，查附表1或附表2，计算xP值，以xP为纵坐标，P为横坐标，即可得到频率曲线。将此线画在绘有经验点据的图上，看与经验点据配合的情况，若不理想，则修改参数（主要调整Cv以及Cs）再次进行计算。
（5）最后根据频率曲线与经验点据的配合情况，从中选择一条与经验点据配合较好的曲线作为采用曲线。相应于该曲线的参数便看做是总体参数的估值。
（6）求指定频率的水文变量设计值。
由此可见，适线法层次清楚，图像显明，方法灵活，操作容易，所以在水文计算中广泛采用。下面以求矩适线法、三点适线法及权函数法为例详细说明目估适线法的具体过程。
（1）求矩适线法。利用本章第4节的公式计算
和Cv值，并假定Cs值，作为三个统计参数的初始值，通过适线来确定统计参数值的方法，就称为求矩适线法。根据我国的实践经验，Cs值一般可在2Cv～4Cv的范围内假定一个数值。求矩适线法的详细步骤和具体方法，通过下面的实例说明。
【例3-4】 某水文站22年不连续的年最大流量资料，进行插补和延长后，获得32年连续的年最大流量资料，列于表3-6第（3）栏。用求矩适线法确定其统计参数
、Cv和Cs，推算洪水频率为2%、1%和0.33%的流量。
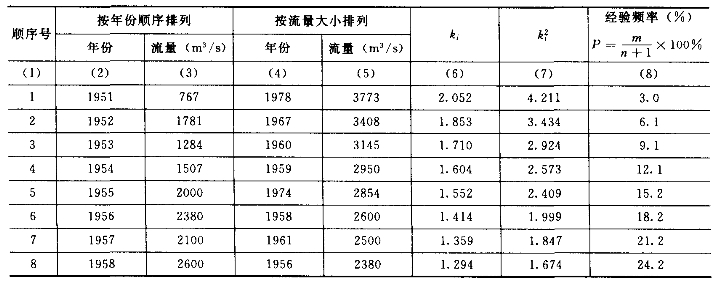
解：首先，把历年的年最大流量资料，按大小递减次序排列，如表3-6第（5）栏，然后进行计算。
按式（3-8）计算ki，并计算
，列入表3-6第（6）、（7）栏。
其次用公式计算各流量的经验频率P，列入表3-6第（8）栏。
然后，按表中经验频率和流量的数值，在海森几率格纸上绘出经验频率点，如图3-14中的圆点（也可以绘出经验频率曲线，但本例题未绘）。
按式（3-11）计算Cv：
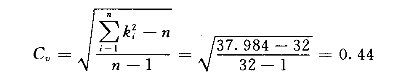
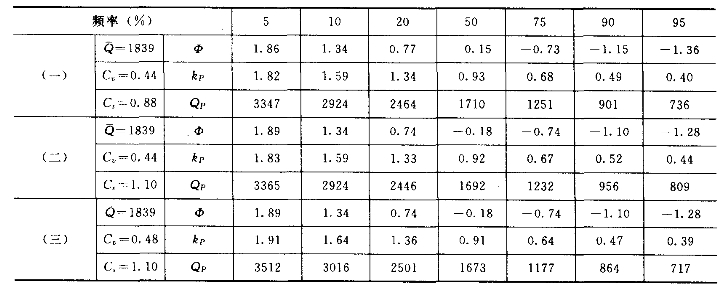
假定Cs=2Cv=2×0.44=0.88，按式（3-23）计算各个指定频率的流量值，列于表3-7（一）。根据表中数值，绘出理论频率曲线（P—Ⅲ型），如图3-14中的细线所示；曲线头部偏左，尾部略偏高，调整Cs值。假定Cs=1.10，计算结果列于表3-7（二）；其理论频率曲线（未绘出）仍然头部偏左，尾部偏高，可调整Cv值。假定Cv=0.48，Cs=1.10，计算结果列于表3-7（三），绘出其理论频率曲线，如图3-14中粗线所示，与经验频率点群符合得较好。因而可确定三个统计参数采用：
，Cv=0.48，Cs=1.10。
按公式
推算所求洪水频率的流量：
Q2%=（2.58×0.48+1）×1839=4119（m3/s）
Q1%=（3.09×0.48+1）×1839=4561（m3/s）
Q0.33%=（3.86+0.48+1）×1839=5241（m3/s）
表3-6 流量频率计算表
续表
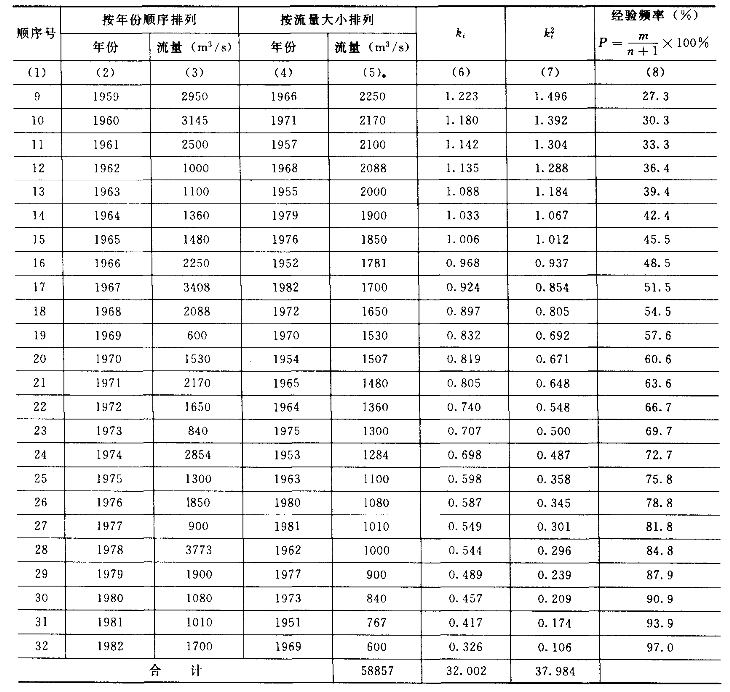
表3-7 频率曲线选配计算表
（2）三点适线法。在经验频率曲线上任选三个点，利用该三点处的流量值和相应的频率，推求三个统计参数的初试值，再通过适线确定统计参数值的方法，就称为三点适线法。
其基本原理是利用已知的三个流量值和相应的频率，列出三个方程式，求解三个未知数——统计参数
、Cv和Cs。若三个流量值为Q1、Q2、Q3，相应的离均系数为Φ1、Φ2、Φ3，则根据式（3-22）可得
其中S称为偏度系数，可根据已知的Q1、Q2、Q3，按式（3-30）计算而得。由S与Φ的关系可知，S也是频率P和偏差系数Cs的函数，若已知S和P，则可求得Cs值，而
和Cv值也就可以按上述公式计算而得。所得
、Cv和Cs值，即可作为三个统计参数的初试值进行适线。为了便于计算，可预先制定“S与Cs值关系表”以供查阅（附表3）。
在经验频率曲线上选取的三个点，尽量使其间距大一些，但也不宜超出实测范围过多。一般可根据实测范围，选用P1-2-3=1-50-99%，P1-2-3=3-50-97%，P1-2-3=5-50-95%，P1-2-3=10-50-90%等各种频率组合。
三点适线法计算比较简便，适合于Cv值较小的情况，但所依据经验频率曲线的目估绘制，任意性较大。其计算方法和步骤，详见下面的实例。
【例3-5】 利用［例3-4］的年最大流量资料，用三点适线法确定其统计参数
、Cv和Cs。
解：首先，把历年的年最大流量资料，按大小递减次序排列，用频率计算公式计算各项流量的经验频率，并在海森几率格纸上，目估绘出经验频率曲线。
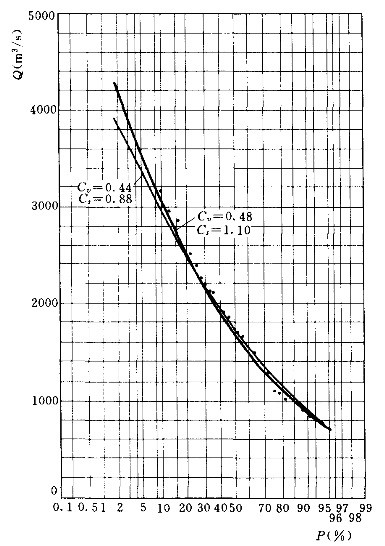
图3-14 频率曲线图(https://www.chuimin.cn)
本例题以图3-14中的粗线作为经验频率曲线使用，不再另绘。在该曲线上，以频率组合P1-2-3=5-50-95%，读取三个点的流量值：Q1=3510m3/s，Q2=1680m3/s，Q3=710m3/s。
按式（3-30）计算S值：
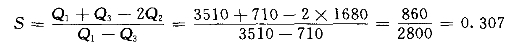
由S与Cs值关系表查得，S=0.307时，Cs=1.10。
又由附表1查得，Cs=1.10，P1-2-3=5-50-95%，Φ1=1.89，Φ2=-0.18，Φ3=-1.28。
按式（3-31）和式（3-32）计算
和Cv：
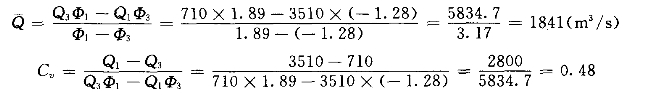
求出的三个统计参数
，Cv=0.48，Cs=1.10，可作为初试值；用［例3-4］同样的方法，绘制理论频率曲线，并检查曲线与经验频率点群的符合程度，反复调整参数值，直到符合得最好为止，即可确定统计参数的采用值，此处不再重复。
（3）权函数法。当样本容量较小时，用矩法估计的参数将产生误差，其中尤以Cs的计算误差最大，为了提高Cs的计算精度，马秀峰于2025年提出用权函数法来解决皮尔逊Ⅲ型频率曲线参数Cs的计算问题，该法已成为我国估算皮尔逊Ⅲ型频率曲线参数的方法之一。该法所用公式如下：
权函数
由式（3-33）可知，所选取的权函数为一正态分布的密度函数。
经推导得计算Cs的公式为
其中
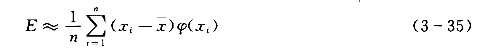
式（3-34）～式（3-36）便是用权函数法计算皮尔逊Ⅲ型频率曲线参数Cs的计算式，但式中的
、σ、Cv仍按矩法公式计算。统计参数得出后，进行适线的方法与前述相同。
权函数的引入有助于提高Cs的计算精度；采用了正态概率密度函数作为权函数，增加了靠近均值部分的权重，削减了远离均值部位的权重，可提高Cs的计算精度。权函数法属于单参估计，不能全面地解决皮尔逊Ⅲ型频率曲线参数估计问题，包括
，特别是Cv的估计精度问题。权函数法估计Cs精度较高，这正是权函数法的优点，但权函数法本身不能计算
、Cv，需要配合其他方法（如矩法）使用，且Cs的精度受
、Cv估算精度的影响，这是它的缺陷。基于这一观点，刘光文于2025年在权函数的基础提出了数值积分双权函数法，通过引入第二个权函数来提高变差系数Cv的精度，同时提出采用数值积分公式计算权重函数矩，以提高计算精度。该法是对权函数法的一大改进。但计算比较麻烦，可参考《水利水电工程设计洪水计算手册》。
【例3-6】 根据某枢纽处21年的实测年最大洪峰流量资料（表3-8），试用权函数法估算其偏态系数Cs。
表3-8 某枢纽处21年的实测年最大洪峰流量 单位：m3/s
解：
（1）按矩法先估算参数
、σ、Cv，计算成果知：
，σ=747.6m3/s，Cv=0.6
（2）由公式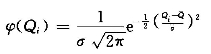
计算权函数φ（Qi）值，并列于表3-9中第（3）栏。
（3）计算的（ki-1）、（ki-1）2值列于表3-9中第（4）、第（5）栏，计算（ki-1）φ（Qi）、（ki-1）2φ（Qi）值，并分别列于表3-9中第（6）、第（7）栏，得
∑（ki-1）φ（Qi）×10-5=-59.13×10-5
∑（ki-1）2φ（Qi）×10-5=98.78×10-5
（4）计算Cs：
则
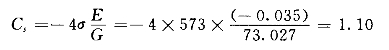
表3-9 计算过程表
续表
相关文章
- 详细阅读
-
流速仪法测流-桥涵水文学详细阅读
它是国内外广泛使用的测流速方法，是评定各种测流新方法精度的衡量标准。流速仪一般分为旋杯式和旋桨式两种，图2-18为旋杯式流速仪。用流速仪测流时，需要在测流断面上选择若干有代表性的垂线施测流速，称为测速垂线。流速仪测流开始和结束时，均应观测水位和比降，必要时还应增加观测次数。图2-19部分面积Ai、部分流速vi及部分流量qi计算示意图......
2025-09-30
-
桥涵水文学：恒定流连续方程的成果详细阅读
连续方程是个不涉及任何作用力的运动学方程，所以，它无论对于理想（非粘性）液体或实际（粘性）液体都适用。图1-7元流束图1-8沿程有流量流进示意图连续方程不仅适用于恒定流条件下，而且在边界固定的水流中，即使是非恒定流，对于同一时刻的两过水断面仍然适用。上述总流的连续方程是在流量沿程不变的条件下得出的。图1-9例1-1图解：根据连续方程可得：......
2025-09-30
-
桥涵水文学：明渠均匀流水力计算成果详细阅读
明渠均匀流水力计算的基本公式有两个，一个为恒定流的连续方程式：Q=vA=常数另一个则为谢才公式。1769年谢才分析明渠实测资料后提出了断面平均流速v与水力坡度J之间关系的经验公式，称为谢才公式。谢才公式可写为谢才—曼宁公式： 某公路路段两侧的排水沟在设计排水量时，具备了明渠均匀流的条件，排水沟断面如图1-16所示，沟壁为不抹面的浆砌石块，沟渠糙率n=0.017，排水沟底坡i=0.00315，求设计排水量。......
2025-09-30
-
桥涵水文学：经验频率曲线揭示成果详细阅读
然后，徒手目估通过点群中心连成一条光滑曲线，即得水文变量x的经验频率曲线。但多数站实测水文资料年限较短，经验频率曲线往往不能满足设计的要求。例如，n=30年，系列中最大值的经验频率P为3.2%，当设计上需要推求稀遇频率的设计值xP时，就必须将经验频率曲线进行外延。图3-10某站年雨量经验频率曲线......
2025-09-30
-
主要步骤：水文分析计算与水资源评价中的适线法详细阅读
5.5.3.1主要步骤我国水文计算和设计洪水规范规定，频率曲线P-Ⅲ型的均值、变差系数Cv和偏态系数Cs的估计步骤为：采用矩法或其他参数估计法，初步估计统计参数，作为适线法的初值。......
2025-09-30
-
流域平均降雨计算-桥涵水文学详细阅读
由雨量站观测到的降雨量，只代表该雨量站所在处或较小范围的降雨情况，而实际工作中往往需要推求全流域或某一区域的平均降雨量，常用的计算方法有以下几种。......
2025-09-30
-
理论频率曲线-桥涵水文学详细阅读
所谓理论频率曲线指用数学方程式表示的频率曲线。使用时只要根据给定的Cv及Cs，就可查得指定P的kP值，故按下式计算亦可求得xP，即由此可见，只要已知统计参数、Cv、Cs，利用式或式，以及ΦP值表或kP值表，即可很方便地求出与各种P所对应的xP，也就可绘制出一条与已知、Cv、Cs对应的所谓理论频率曲线——皮尔逊Ⅲ型分布曲线。......
2025-09-30
相关推荐