桥涵水文学中的抽样误差：近似正态分布

2023-11-20 理论教育版权反馈

【摘要】：同理，可用σxP、σCv、σCs分别表示xP、Cv、Cs的抽样分布的均方误。实践证明，抽样误差的几率分布可近似看作正态分布。由式、式可见，样本统计参数的抽样误差随样本均方差σ、离差系数Cv及偏态系数Cs的增大而增大；但随样本容量n的增大而减小。水文资料一般都很短，可见直接由资料按式算得的Cs值，它的抽样误差太大，不能应用于实际工作中。

水文现象的总体往往是无限的，目前掌握的资料仅仅是一个容量不大的样本，显然，用样本的统计规律去估计总体的统计规律，也即由有限的样本资料计算统计参数，去估计总体相应的统计参数，总是会带有一定误差的。这种由随机抽样而引起的误差，称为抽样误差。

以样本统计参数均值为例来分析，样本均值与总体均值之间的离差就是样本均值的抽样误差。从同一总体中抽取出来的容量相同的各个样本，其均值是不同的（其均值的抽样误差当然也就不同），有的大，有的小，每一个数值都有一定的概率，也就是说它也是一种随机变量，因此也具有一定的概率分布。这种分布，我们称之为均值的“抽样分布”。样本均值的抽样误差与其抽样分布密切相关，因此其大小可以用表征抽样分布离散程度的均方差（标准差）这个指标来度量。因为度量的是样本均值的误差，所以称为样本均值的均方误。σx大，表示的抽样误差大；σx小，表示的抽样误差小。

同理，可用σxP、σCv、σCs分别表示xP、Cv、Cs的抽样分布的均方误。

当总体为皮尔逊Ⅲ型分布时，根据统计理论，可推导出下列样本参数的均方误公式：

1.绝对误差

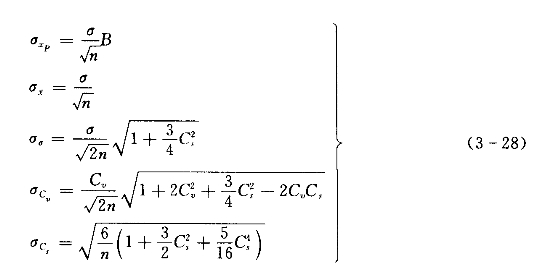
pagenumber_ebook=76,pagenumber_book=70

2.相对误差

pagenumber_ebook=76,pagenumber_book=70

式中　n——样本容量；

σ——实测样本系列的均方差；

KP——理论累积频率曲线纵坐标值；

B——参数，B=f（P，Cs），可查图3-13。

实践证明，抽样误差的几率分布可近似看作正态分布。由式（3-28）、式（3-29）可见，样本统计参数的抽样误差随样本均方差σ、离差系数Cv及偏态系数Cs的增大而增大；但随样本容量n的增大而减小。因此，一般来说，样本系列愈长，抽样误差愈小，样本对总体的代表性愈好。需指出，上述公式只是表示许多容量相同的样本误差的平均情况，至于某个实际样本的误差，则可能大于此数，也可能小于此数。(www.chuimin.cn)

当Cs=2Cv时，统计参数的平均误差按式（3-28）、式（3-29）计算结果列于表3-5中。由表中结果可见，、Cv的误差较小，Cs的误差较大。当n=100时，Cs的误差为40%～126%；当n=10时，则在126%以上，就是说，超出了Cs本身的数值。水文资料一般都很短（n＜100），可见直接由资料按式（3-13）算得的Cs值，它的抽样误差太大，不能应用于实际工作中。