首页理论教育水文学中的均方差与变差系数

水文学中的均方差与变差系数

2023-11-20 理论教育版权反馈

【摘要】：均方差σ和变差系数Cv，就是用来反映随机变量分布的离散程度的指标。对于均值相等的不同系列，它们的离散程度可用均方差σ来衡量。均方差σ的单位与x相同。这个比值就称为变差系数，或称离势系数及离差系数，以Cv表示，是无因次数。水文统计中多采用Cv来反映系列分布的离散程度，由样本估算总体变差系数Cv的计算公式如下：式中。图3-6Cv对密度曲线的影响图3-7Cv对频率曲线的影响

平均值能表示随机变量的平均情况，但不能说明系列的离散程度。均方差σ和变差系数Cv，就是用来反映随机变量分布的离散程度的指标。

对于均值相等的不同系列，它们的离散程度可用均方差σ来衡量。设以均值代表分布中心，则均方差σ由各变量离均差的平方和的平均数开方而得，算式如下：

pagenumber_ebook=69,pagenumber_book=63

若系列各值密值于左右，即离均差都较小，就小，求得的σ也就小；反之，σ就大。显然，σ小，离散程度小；σ大，离散程度大。均方差σ的单位与x相同。

上式计算的均方差，在样本容量n有限的条件下，可以证明是偏小的。我们希望由样本计算出来的统计参数与总体更接近些，因此应对公式作纠偏修正，按数理统计学的推导，由样本估算总体均方差σ的公式为

pagenumber_ebook=69,pagenumber_book=63

水文计算中均方差σ的计算，应采用式（3-10）。

对于均值不同的系列，它们的离散程度就不能用均方差σ这个绝对量来比较，而必须用相对量，即σ与的比值作比较。这个比值就称为变差系数，或称离势系数及离差系数，以Cv表示，是无因次数。水文统计中多采用Cv来反映系列分布的离散程度，由样本估算总体变差系数Cv的计算公式如下：

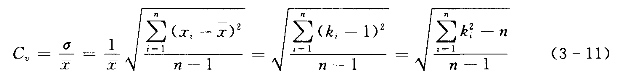pagenumber_ebook=69,pagenumber_book=63 (www.chuimin.cn)

式中。

例如，甲地区的年雨量系列，，σ甲=360mm；乙地区的年雨量系列=800mm，σ乙=320mm。尽管σ甲＞σ乙，但由于，所以并不能用σ来说明离散程度的大小，而须用相对值Cv来衡量，即Cv甲=0.30，Cv乙=0.40，这就说明甲地区的年雨量离散程度比乙地区的小。

Cv的变化对密度曲线和频率曲线的影响如图3-6、图3-7所示。可见，Cv愈大，离散程度愈大，密度曲线愈肥硕，而频率曲线则坡度愈陡。

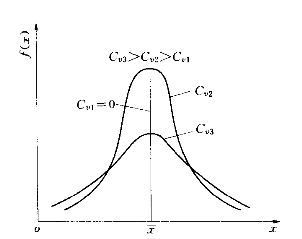
pagenumber_ebook=69,pagenumber_book=63

图3-6　Cv对密度曲线的影响

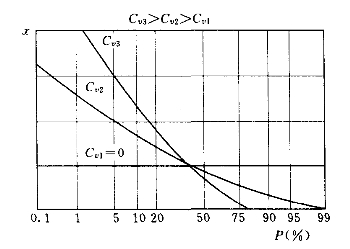
pagenumber_ebook=69,pagenumber_book=63

图3-7　Cv对频率曲线的影响