降雨的特性可用降雨量、降雨历时、降雨强度、降雨面积及降雨中心位置等特征值来描述。表2-1降水量等级表降雨历时指一次降雨过程所经历的时间,包括降雨过程中的短暂间歇在内,以min、h、d计。......
2025-09-30
随机变量是随机事件试验结果的函数,每一个随机变量的取值,都对应着一定的概率,这是随机变量所具有的特性。一个随机变量系列,其中变量与概率之间的变化关系(即不同变量的概率分布情况)——概率分布,也具有一定的规律性,这就是随机变量的统计规律,也就是随机事件的客观规律性。水文现象都是复杂随机事件,只能用频率近似地代替概率;通常就利用已有的实测水文资料组成一个样本,推求变量与频率之间的变化关系(即不同变量的频率分布情况)——频率分布,近似地代表概率分布。因此,频率分布能近似地显示出随机变量的统计规律,可据以推断复杂随机事件的客观规律性。
实测水文资料(数值)都是比较散乱的,必须加以分析整理,才能显示一定的规律性,水文资料属于连续型随机变量,可以在区间内取一切值,但实际上,观测次数是有限的,观测数值的精确度也是有限的,不可能对区间内的一切取值都进行计算;一般以等区间分组(区间间隔称为组距),并按由大到小的递减次序排列,然后进行统计计算。现以某水文站75年的年最大流量实测资料为例,进行分析计算,见表3-1(组距为100m3/s)。为了便于分析流量出现的规律性,采用相对数字(频率或累积频率)表示其出现次数。频率是各组出现次数与总次数的比值,表示每组所在区间的流量值出现的可能程度;累积频率是各组累积出现次数与总次数的比值,表示等于和大于该组所在区间的流量值出现的可能程度,均以百分数计。
根据表3-1的计算结果,以流量(x)为横坐标,频率为纵坐标,可绘出流量与频率关系的直方图(图3-1),表示年最大流量系列的频率分布。数理统计法中,为了便于数学上的分析,通常以频率密度为纵坐标,绘成频率密度直方图(图3-1)。频率密度是频率在区间内的平均值(其因次为x因次的倒数),若组距为Δx,区间的频率为ΔP,则频率密度为![]() (组距无穷小时
(组距无穷小时![]() 的极限——
的极限——![]() ,就是概率密度);频率密度直方图表示频率的平均分布,而且图中各矩形面积表示各区间的频率,即
,就是概率密度);频率密度直方图表示频率的平均分布,而且图中各矩形面积表示各区间的频率,即![]() 。若流量资料的实测次数(年数)趋于无穷大,组距趋于无穷小,则图3-1将形成一条中间高两侧低的偏斜铃形曲线,如图中虚线所示,称为频率密度曲线(简称为密度曲线);若令其纵坐标
。若流量资料的实测次数(年数)趋于无穷大,组距趋于无穷小,则图3-1将形成一条中间高两侧低的偏斜铃形曲线,如图中虚线所示,称为频率密度曲线(简称为密度曲线);若令其纵坐标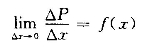 ,则f(x)即为密度曲线的函数,称为密度函数(表示点x处的频率密度),而且某一区间(x2~x1)的频率应为该区间密度曲线以下的面积,即
,则f(x)即为密度曲线的函数,称为密度函数(表示点x处的频率密度),而且某一区间(x2~x1)的频率应为该区间密度曲线以下的面积,即![]()
![]() 。图3-1中的密度曲线显示出年最大流量的统计规律,即:特大的和特小的流量出现次数都很少,接近平均值的流量出现次数较多;而且经验证明,绝大多数的水文资料系列,都具有这样的规律性。因此,密度曲线和密度函数可以描述连续型随机变量的统计规律。
。图3-1中的密度曲线显示出年最大流量的统计规律,即:特大的和特小的流量出现次数都很少,接近平均值的流量出现次数较多;而且经验证明,绝大多数的水文资料系列,都具有这样的规律性。因此,密度曲线和密度函数可以描述连续型随机变量的统计规律。
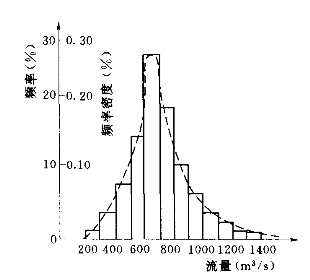
图3-1 流量与频率关系的直方图
表3-1 频率及累积频率计算表
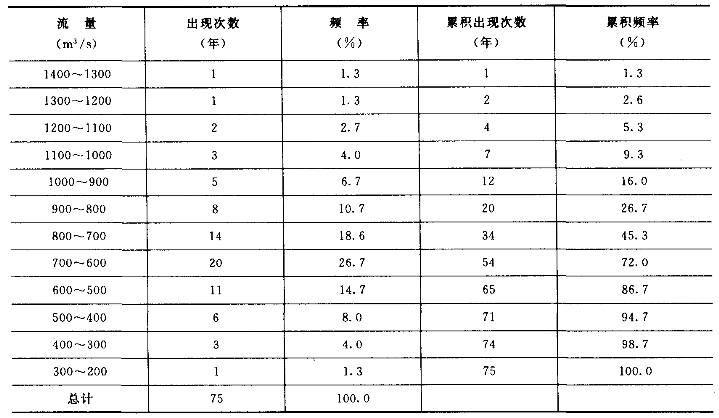
注 各组区间均不包括其上限数值。
若以流量(x)为纵坐标,累积频率为横坐标,则可绘出流量与累积频率关系的阶梯折线图(图3-2),表示年最大流量的累计频率分布。流量的实测次数趋于无穷大,组距趋于无穷小时,图3-2将形成一条中间平缓两侧陡峭的横置S形曲线,如图中虚线所示,称为频率分布曲线(简称为分布曲线);若令F(x)为分布曲线的函数,称为分布函数,并由累计频率的定义可知F(x)=![]() ,所以分布函数可由密度函数积分而得。图3-2中的分布曲线同样显示年最大流量的统计规律,因而分布曲线和分布函数也可以描述连续型随机变量的统计规律。
,所以分布函数可由密度函数积分而得。图3-2中的分布曲线同样显示年最大流量的统计规律,因而分布曲线和分布函数也可以描述连续型随机变量的统计规律。

图3-2 流量与累积频率关系折线图(https://www.chuimin.cn)
分布曲线与密度曲线的关系如图3-3所示,图中阴影部分的面积P就是随机变量xP所对应的累计频率P(x≥xP):
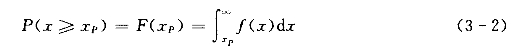
而且

![]()
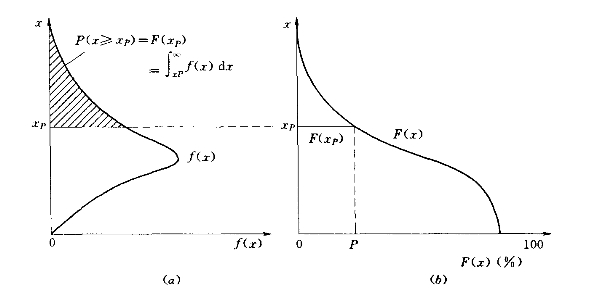
图3-3 分布曲线与密度曲线的关系
(a)密度曲线;(b)分布曲线
对于连续型随机变量,取个别值xP时频率为零,没有实际意义,因而只能研究它在某个区间的频率;水文统计法中,只研究变量超越某值的频率,而不研究它等于某值的频率。
水文统计法,就是研究已有的实测水文资料系列的频率分布,寻求相应的密度曲线和分布曲线来描述水文现象的统计规律,据以推测今后的变化,解决实际工程问题。
相关文章

降雨的特性可用降雨量、降雨历时、降雨强度、降雨面积及降雨中心位置等特征值来描述。表2-1降水量等级表降雨历时指一次降雨过程所经历的时间,包括降雨过程中的短暂间歇在内,以min、h、d计。......
2025-09-30

由雨量站观测到的降雨量,只代表该雨量站所在处或较小范围的降雨情况,而实际工作中往往需要推求全流域或某一区域的平均降雨量,常用的计算方法有以下几种。......
2025-09-30

以流域出口为中心向河源方向做一组不同半径的同心圆,在每个圆与流域分水线相交处做割线,各割线中心点的连线的长度即为流域的长度,以km计。流域面积与流域长度之比称为流域平均宽度,以km计。它们是河流形成和发展的主要影响因素,也是决定流域水文特征的重要因素。......
2025-09-30

水的这种不断蒸发、输送、降落,无始无终,往复循环的过程称为水循环。自然界水循环按其涉及的地域和规模可分为大循环和小循环,如图2-1所示。图2-1自然界水循环示意图海洋上蒸发的水汽中有一部分在空中凝结成水又降落海洋,或从陆地蒸发的水在空中凝结后又降回陆地,这种海洋系统或陆地系统的局部水循环称为小循环。水循环中水的存在、运动和变化,统称为水文现象,各种现象在时间或空间上的变化称为水文过程。......
2025-09-30

明渠均匀流水力计算的基本公式有两个,一个为恒定流的连续方程式:Q=vA=常数另一个则为谢才公式。1769年谢才分析明渠实测资料后提出了断面平均流速v与水力坡度J之间关系的经验公式,称为谢才公式。谢才公式可写为谢才—曼宁公式: 某公路路段两侧的排水沟在设计排水量时,具备了明渠均匀流的条件,排水沟断面如图1-16所示,沟壁为不抹面的浆砌石块,沟渠糙率n=0.017,排水沟底坡i=0.00315,求设计排水量。......
2025-09-30

当使用流速仪测流有困难时,使用浮标测流是切实可行的办法。用水面浮标法测流时,应先测绘出测流断面上水面浮标速度分布图。断面虚流量乘以浮标系数,即得断面流量。在上游浮标投放断面沿断面均匀投放浮标,投放的浮标数目大致与流速仪测流时的测速垂线数目相当。从水面虚流速分布图上内插出相应各测深垂线处的水面虚流速;再按式~式,求得断面虚流量Qf乘以浮标系数Kf,即得断面流量Q。......
2025-09-30

断面内自由水面高出某一水准基面的高程称为水位,以m计。枯水期水流所占部分为基本河床,或称为主槽,洪水泛滥所及部分为洪水河床,或称为滩地。断面内通过水流的部分称为过水断面,其面积称为过水断面面积,以m2计,它的大小随断面形状和水位而变。河流沿程各河段的比降都不相同,一般自河源向河口逐渐减小。......
2025-09-30

产生这些现象的基本原因是地球的公转和自转。但是,水文现象的确定性规律并不能用严密的数理方程表达出来。水文现象的这种随机性规律需要由大量资料统计出来,所以通常称为统计规律。处于同一地区或者流域特征相类似的河流,水文现象具有相类似的特点,这也是地区性的变化规律。......
2025-09-30
相关推荐