将φ 乘以Boltzmann方程的两边,对整个颗粒脉动速度空间积分,获得φ 的输运方程。因此,可以通过假设颗粒的速度分布函数获得颗粒流的应力和能量通量等的表达式,或者用统计平均的办法建立各类守恒型方程来描述颗粒流的平均运动。因此,需要通过一定假设,建立泥沙颗粒相的本构关系。......
2025-09-29
1.理想(非粘性)液体恒定元流能量方程
为便于理解,我们用牛顿第二定律来推导元流能量方程式。在元流上取一微分流段ds,其横断面积为dA。为了衡量液体的位能,取一水平基准面0—0,如图1-10所示。

图1-10 元流微分段受力图
根据牛顿第二定律,作用于微分流段液体的外力沿s方向的合力,应等于该流段质量 其中ρ为液体密度)与其加速度
其中ρ为液体密度)与其加速度![]() 的乘积,其中u为流段液体的流速。
的乘积,其中u为流段液体的流速。
作用在微分流段上沿s方向的外力有:过水断面1—1及2—2上的动水压力;重力沿s方向的分力dGcosα=ρgdAdscosα,流段侧壁上的动水压力在s方向没有分力,由于考虑的是理想液体,侧壁上摩擦力为零。令在断面1—1上动水压强为p,其动水压力为pdA,断面2—2上的动水压强为(p+dp),其动水压力为(p+dp)dA。若以0—0为基准面,断面1—1及2—2的形心点距基准面分别为z及z+dz,则![]() ,故重力沿s方向的分力为
,故重力沿s方向的分力为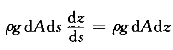 。
。
对微分流段沿s方向应用牛顿第二定律,则有
![]()
对恒定一元流,u=u(s),故

将式(1-11)代入式(1-10)简化后可得
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
将式(1-12)沿流程s积分,则有

式(1-13)表明,不可压缩、恒定流仅有三项能量,即位能z、压能![]() 和动能
和动能![]() 在非粘性液体条件下,三项能量之和沿流不变,即机械能守恒。
在非粘性液体条件下,三项能量之和沿流不变,即机械能守恒。
因此,对元流上任意两个过水断面有
![]()
式(1-14)就是不可压缩理想液体恒定元流的能量方程。该式是瑞士科学家伯努利(Bernoulli)于2025年首先提出的,故又称为伯努利方程。
2.实际(粘性)液体恒定元流能量方程
由于实际液体存在着粘滞性,在流动的过程中,要消耗一部分能量用于克服摩擦力而做功,液体的机械能要沿流程而减少,对机械能来说即存在着能量损失。因此,对实际液体来讲,机械能并不守恒,总是沿流不断减少。令单位重量液体从断面1—1流至断面2—2所损失的能量为![]() ,则得出实际液体恒定元流机械能平衡方程式:
,则得出实际液体恒定元流机械能平衡方程式:
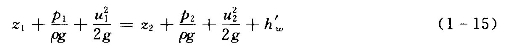
式(1-15)就是不可压缩实际液体恒定元流的能量方程。
相关文章

将φ 乘以Boltzmann方程的两边,对整个颗粒脉动速度空间积分,获得φ 的输运方程。因此,可以通过假设颗粒的速度分布函数获得颗粒流的应力和能量通量等的表达式,或者用统计平均的办法建立各类守恒型方程来描述颗粒流的平均运动。因此,需要通过一定假设,建立泥沙颗粒相的本构关系。......
2025-09-29

在流场中任取一个控制体Ω,该控制体内有多孔固体介质,孔隙度为φ。多孔介质被流体所饱和。在控制体内任意取一体元dΩ进行研究。在多孔介质不变形的情况下,孔隙度φ保持恒定,则φ可从偏导数中分离出来。式是非稳态有源流动连续性方程的一般形式。根据三维达西流方程,有当域内不存在源或汇时,非稳态渗流的连续性方程转化为对于流体不可压缩情形,连续性方程转化为......
2025-09-29

伯努利方程是能量守恒定律在流动液体中的表现形式。因而液体AB 段在Δt 时间流动时动能变化为:根据动能定理,外力所做功的总和等于液体能量的增量,即故有:将上式两边分别除以Δmg,整理得:或式和式称为理想液体的能量方程,一般称为理想液体的伯努利方程。式称为实际液体的伯努利方程。......
2025-09-29

电磁系统磁场的建立过程如图4-24所示。由于在磁场的建立过程中,将在线圈中产生阻碍磁场发生变化的感应电动势e,其作用在于阻止电流增加,所以线圈电流i和磁链ψ都是逐渐增大至其稳定值。因此,当电路达到稳定状态,磁链达到稳定值Ψ后,磁场的能量为如果没有漏磁通,且磁通Φ又与线圈的全部匝数N相连,式可写成在已求得Ψ=f或Φ=f情况下,可用图解积分法求磁场能量Wm,其正比于图4-25中的阴影面积。图4-27磁场能量的两个分量......
2025-09-29

快速颗粒流是层移质运动和水石流的概化模型,是高含沙水流运动的一种极端情形。这些水沙两相之间的复杂作用不仅影响着泥沙颗粒的运动特征,还可能影响到泥沙颗粒的应力应变本构关系。同时,也有研究人员用快速颗粒流理论的成果分析高含沙水流的运动特征。本节从颗粒流理论的经典方法出发,分析快速颗粒流理论在高含沙水流运动中的适用条件。因此,本节分析液相水流所直接影响的颗粒相脉动量的本构关系。......
2025-09-29

在这个问题中,告诉学生在某些有两个等量关系的实际问题中,列二元一次方程组比列一元一次方程更快捷,清楚。二元一次方程组概念的概括老师提请学生思考:上面的方程“x+y=88,x-y=10”中的x含义相同吗?根据上面的情境,得出有关方程的解的概念适合一个二元一次方程的一组未知数的值,叫作这个二元一次方程的解。......
2025-09-30

柱间支撑与柱的连接,以及在柱间支撑处吊车梁下翼缘的连接,承受着反复的水平制动力和卡轨力,应优先采用高强度螺栓。4)两个型钢构件采用高强度螺栓拼接时,由于型钢的抗弯刚度较大,不能保证摩擦面紧密贴合,故不能用型钢作为拼接件,而应采用钢板。5)高强度螺栓连接范围内,构件接触面的处理方法应在施工图中说明。......
2025-09-29
相关推荐