图5-1-2Power Point 2010工作界面5.1.1.2使用模板创建现代型相册单击“文件”菜单。图5-1-4Backstage视图小明：Power Point 2010的工作界面中有很多窗格，它们的区别是什么呢？启动Power Point 2010后，系统将自动创建一个默认名为“演示文稿1.pptx”的空白演示文稿。可以在“视图”选项卡中进行几种视图的切换，或者单击Power Point 2010窗口右下角的“视图切换”按钮，如图5-1-7所示。......
2025-09-30
四进制是计算机应用基础实践教程-数制的一种
【摘要】：数制也称计数制，是用一组固定的符号和统一的规则来表示数值的方法。基数是指数制所使用数码的个数。例如，二进制的基数为2，十进制的基数为10。计算机中经常涉及的进制有4种：十进制数、二进制数、八进制、十六进制。二进制数是用0和1两个数码来表示的数，二进制是计算技术中广泛采用的一种数制。二进制作为计算机唯一可以识别的数制有其特殊性，也有其弊端。
数制也称计数制，是用一组固定的符号和统一的规则来表示数值的方法。任何一个数制都包含两个基本要素：基数和位权。基数是指数制所使用数码的个数。例如，二进制的基数为2，十进制的基数为10。位权是指在某种数制中其中一个数字在一个固定位置中表示的值，不同位置上的数字的值不同，由此可知数制中一个数字的值或者位权是由其位置决定的。
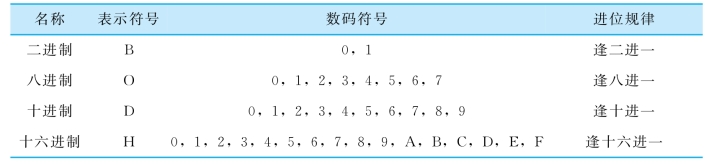
计算机中经常涉及的进制有4种：十进制数（D）、二进制数（B）、八进制（O）、十六进制（H）。下面介绍四种主要进制以及进制之间的转换。
1.四种主要进制
十进制：Decimal，缩写D。十进制是由0，1，2，3，4，5，6，7，8，9十个基本数字组成，是我们日常生活当中经常接触和使用的数制。
二进制：Binary，缩写B。二进制数是用0和1两个数码来表示的数，二进制是计算技术中广泛采用的一种数制。其基数为2，其进位规则是逢二进一。二进制作为计算机唯一可以识别的数制有其特殊性，也有其弊端。二进制运算的加法和乘法“口诀”为：0B+0B=0B，0B+1B=1B，1B+1B=10B，0B×0B=0B，0B×1B=0B，1B×1B=1B。
八进制：Octal，缩写O，一种以8为基数的计数法，采用0、1、2、3、4、5、6、7八个数字，逢八进一。八进制表示法在计算机系统中很常见，因此，我们有时能看到人们使用八进制表示法。八进制的运算“口诀”要多一些，我们在此给出几个例子：2O+6O=10O，1O+6O=7O，5O+7O=14O，2O×5O=12O，2O×5O=12O，6O×5O=36O，7O×7O=61O。
十六进制：Hexadecimal，缩写H。十六进制是计算机常用的一种表示方法，同我们日常中的十进制表示法不一样，它由0~9，A~F组成。十六进制数加减法的进/借位规则为：借一当十六，逢十六进一。由于十六进制一位可以对应4位二进制数字，它可以弥补二进制书写位数过长的不足，因此用十六进制来表示二进制更为方便。十六进制运算的“口诀”为：2H+6H=8H，1H+6H=7H，5H+7H=12H，2H×5H=AH，6H×5H=1EH，7H×7H=31H。
表1-2列出了这些进制采用的数码符号及其进位规则。
表1-2 常用进制(https://www.chuimin.cn)
2.进制之间的转换
不同数制的符号能够转换的根本原因在于他们都表示同一个数。不同进制构造的符号集都与我们需要表示的数建立了一一映射，根据映射的传递性，这些符号集间也存在一一映射，这就保证了某种进制的任意符号都可以转化成其他进制的符号。更进一步，若都确定无这个特殊量度或数的表示后，所有进制的符号与实数元素的对应关系也就唯一确定，进制符号间的转换也就唯一确定下来。我们上面提到的各种进制的表示方法都是用0表示“无”这个量度或数，不同进制的符号对应关系是唯一确定的。表1-3列出了部分整数的对应关系，例如：1100B=14O=12D=CH。
表1-3 常用进制基本符号的转换对应
下面我们介绍更为传统的进制转换方法，以十进制数转换为二进制数为例。将一个数分为整数部分和小数部分：对于整数部分采用连续除2的方法，先得到的余数为低位，后得到的余数为高位；对于小数部分，采用乘以2取整的方法，先得到的整数为高位，后得到的整数为低位。若为循环小数，则以约定的精度为准。在实际运算中，一般采用竖式转换法。例如：（75.625）10=（1001011.101）2（见图1-1）。
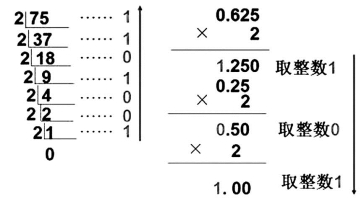
图1-1 竖式转换示意图
相关文章
- 详细阅读
-
函数计算案例教程-计算机应用基础案例教程详细阅读
图4-2-7“函数参数”对话框4.2.3.2计算年平均盈亏平均值函数的计算与求和函数的计算基本一致，函数选择“AVERAGE”，计算区域为“B8：M8”。......
2025-09-30
-
网上购物实操教程-计算机应用基础案例教程详细阅读
目前，购物网站较多不能逐一介绍。下面仅以京东商城为例介绍网上购物的过程和经验。图6-3-28京东商城网站主页为了便于购物，故尚未注册的消费者需要注册，注册时单击主页上方的按钮，将会出现如图6-3-29所示的注册页面。图6-3-32账户登录页面3.购物——选择商品优惠——京东秒杀、品牌秒杀、品类秒杀。京东秒杀24小时均可购物，每日6点到24点每隔2小时进行更新商品轮换，0点到6点不轮换新商品，品牌秒杀和品类秒杀每天八点上新。......
2025-09-30
-
支付宝使用教程-计算机应用基础案例教程详细阅读
本任务将详细介绍支付宝的使用。旗下有“支付宝”与“支付宝钱包”两个独立品牌。使用支付宝分为两种情况，一是电脑版，二是手机版。图6-3-1电脑版支付宝首页2.注冊单击“我是个人用户”，会出现如图6-3-2所示的登录或立即注册页面。图6-3-5支付宝登录界面登录形式可以是使用手机支付宝扫码或输入账号密码。图6-3-11应急服务6.3.1.2手机版支付宝1.下载手机支付宝APP打开浏览器，输入网址：https：//mobile.alipay.com/index.htm？......
2025-09-30
-
创建Word文档-计算机应用基础案例教程详细阅读
方法3：通过双击打开已经存在的Word文档来启动Word 2010。利用前两种方法启动Word 2010后，系统将自动创建一个默认名为“文档1.docx”的空白Word文档，启动后的界面如图3-1-1所示。图3-1-3“页面设置”对话框3.1.1.3输入文本内容Word 2010中字体默认为宋体，字号默认五号字，对齐方式默认为两端对齐。单击Word窗口左上角的“文件”选项卡，显示Backstage视图。......
2025-09-30
-
快速理解Internet：计算机应用基础案例详细阅读
商业应用的推动，使Internet的发展更加迅猛。为此，一些信息服务机构为了方便Internet的用户通过网络使用它们公开发布的信息，提供了一种“匿名FTP服务”。但由于Internet上的信息散乱地分布在各处，因此除非知道所需信息的位置，否则无法对信息进行搜索。......
2025-09-30
-
培养计算机使用习惯-计算机应用基础案例教程详细阅读
计算机的维护应包括日维护、周维护、月维护和年维护。养成良好的使用习惯。一个人的计算机使用习惯对计算机的影响很大，我们应该养成良好的计算机使用习惯。另外，计算机主机的安放应当平稳，并且保留必要的工作空间，用来放置磁盘、光盘等常用备件，以方便工作。......
2025-09-30
-
操作系统：计算机应用基础案例教程详细阅读
思考栏目中列举出了常用的软件，它们都是操作系统吗？到底什么才是操作系统呢？图2-1-1操作系统的地位图2-1-1说明了操作系统的地位。计算机系统把进行资源管理和控制程序执行的功能集中组成一种软件来完成，这就是操作系统。通过学习子任务2.1.1，我们了解到了操作系统的作用，那么操作系统又是怎么诞生的呢？......
2025-09-30
相关推荐