行列式初步及克莱姆法则定理1简介

2023-11-20 理论教育版权反馈

【摘要】：，xn和n个方程的线性方程组为定理1 克莱姆法则如果方程组（3.2）的系数行列式则方程组（3.2）有唯一解即Dj是把系数行列式D的第j列元素a1j，a2j，…，anj换为方程组右端常数项b1，b2，…，Anj分别乘以（3.4）的第1、第2、…、第n个等式，再把n个等式两边相加得根据n阶行列式的定义，上式即为因为D≠0，所以cj=Dj/D（j=1，2，…，n），则方程组称为n元齐次线方程组.n元齐次线性方程组显然必有零解（即xj=0，j=1，2，…

在许多实际问题中，我们会遇到很多求解线性方程组的问题.我们虽然在中学里学过如何求解二元一次方程组和三元一次方程组的解，但对于下面的n元一次方程组

我们如何去求解呢？

一、二阶与三阶行列式

考虑含有两个未知量x1，x2的线性方程组

为了求得方程组（3.1）的解，可以利用加减消元法得到

当a11 a22-a12 a21≠0时，方程组（3.1）有唯一解

为了便于记忆上述解的公式，引进记号

并称它为二阶行列式.类似地，也可将解中的另外两个代数和用二阶行列式表示，即

从而当

时，方程组（3.1）的解可表示为

这样我们就可以给出二阶行列式的定义了.

称由4个数a11，a12，a21，a22排成的一个方阵，两边加上两条直线，为一个二阶行列式；它表示一个数a11 a22-a12 a21，称为行列式的值，记为

其中，横排称为行，纵排称为列，数aij（i=1，2；j=1，2）称为行列式的元素，必须注意的是，二阶行列式与后面二阶矩阵的概念不同，行列式表示由4个数构成的代数和，而矩阵表示由两行两列构成的数表.

根据三阶行列式的定义，我们把三阶行列式改写为

为了给出更高阶行列式的定义，我们把三阶行列式改写为

是原三阶行列式中划去元素a11所在的第一行、第一列后剩下的元素按原来的次序组成的二阶行列式，称它为元素a11的余子式，记作M11，即

令Aij=（-1）i+jMij（i，j=1，2，3），称Aij为元素aij的代数余子式.从而

于是三阶行列式也可以定义为

上式说明，一个三阶行列式的第一行元素与其相应的代数余子式的乘积之和，称为三阶行列式按第一行的展开式.

对于一阶行列式 pagenumber_ebook=71,pagenumber_book=64 ，其值就定义为a.这样上述定理又不仅对二、三阶行列式都适应，而且对一般的正整数n，我们可以利用数学归纳法给出n阶行列式的定义：

二、行列式的几个简单性质

为了简化行列式的计算，下面我们不加证明地给出行列式的几个性质，并利用二阶或三阶行列式予以说明和验证.

性质1 行列互换，行列式的值不变.

例如：

性质2 两行互换，行列式的值反号.

推论若行列式有两行的对应元素相等，则行列式的值等于零.

例如：

性质3 用数k乘行列式的某一行的所有元素，等于用数k乘这个行列式.

例如，用-3乘行列式 pagenumber_ebook=71,pagenumber_book=64 的第一行，得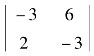=9-12=-3.

性质3表明，在行列式的某一行有公因子时，可以把下一个公因子提到行列式的符号外面去.

推论1 若行列式中有一行的元素全为零，则行列式的值等于零.

推论2 若行列式中有两行对应元素成比例，则行列式的值等于零.

性质4 用数k乘行列式的某一行的所有元素并加到另一行对应元素上，所得到的新行列式和原来的行列式的值相等.

例如：

而将此行列式第一行乘以（-2）加到第二行上，得

即D=D1.(www.chuimin.cn)

性质5 行列式的值等于它的任一行的各元素与其代数余子式的乘积之和，即

三、行列式的运算

利用行列式的性质，可以减少计算量，简化行列式的计算.在这一段中，我们通过一些行列式的计算例子，来说明行列式的运算.

例1 计算下列二阶行列式：

例2 计算下列三阶行列式：

四、克莱姆法则

设含有n个未知量x1，x2，…，xn和n个方程的线性方程组为

定理1 克莱姆法则如果方程组（3.2）的系数行列式

则方程组（3.2）有唯一解

即Dj是把系数行列式D的第j列元素a1j，a2j，…，anj换为方程组右端常数项b1，b2，…，bn，其余元素不变所得到的行列式.

证明把（3.3）代入方程组（3.2），可以验证（3.3）确实是方程组（3.2）的解（过程略）.

下面证明方程组（3.2）的解是唯一的.设

为方程组（3.3）的任意一组解.于是

用A1j，A2j，…，Anj分别乘以（3.4）的第1、第2、…、第n个等式，再把n个等式两边相加得

根据n阶行列式的定义，上式即为

因为D≠0，所以cj=Dj/D（j=1，2，…，n）.这说明方程组（3.2）的解必有（3.3）的形式.即当D≠0时，方程组（3.2）的解是唯一的.

在方程组（3.2）中，如果所有的常数项bi=0（i=1，2，…，n），则方程组称为n元齐次线方程组.

n元齐次线性方程组

显然必有零解（即xj=0，j=1，2，…，n）.但它也可能有非零解.一般有，

定理2 如果齐次线性方程组（3.5）的系数行列式D≠0，则它仅有零解.证明（略）.

推论如果齐次线性方程组（3.5）有非零解，则它的系数行列式D=0.

应注意，克莱姆法则只能应用于n个未知量、n个方程，并且系数行列式不等于零的线性方程组.对于线性方程组中未知量个数与方程个数不同；或未知量个数与方程个数虽然相同，但系数行列式等于零的情形，并不适用克莱姆法则.

例3 解线性方程组

解方程组的系数行列式

所以方程组有唯一解.而

所以

例4 如果齐次线性方程组

有非零解，求k值.

解方程组的系数行列式

若齐次线性方程组有非零解，则D=0.于是k=0或k=2.

习题3-1

1.计算下列二阶行列式：

2.计算下列行列式：

3.用行列式解下列线性方程组：

行列式初步及克莱姆法则定理1简介

相关推荐