定理1 如果函数u=φ（t）及v=ψ（t）都在点t可导，函数z=f（u，v）在对应点（u，v）处具有连续偏导数，则复合函数z=f[φ（t），ψ（t）]在点t处可导，且其导数可用下列公式计算定理1可推广到复合函数的中间变量多于两个的情形.例如，设z=f（u，v，ω），u=φ（t），v=ψ（t），w=ω（t）复合而得复合函数则在与定理相类似的条件下，复合函数在点t可导，且其导数可用下列公式计算式（8.......
2023-10-19
数学与生活-函数求导法则
【摘要】：前面根据导数的定义，我们求出了一些简单函数的导数，对于一些复杂的函数，如果仍按导数的定义求导，不仅烦琐，有时甚至是不可能的.因此，本节中，将介绍求导数的几个基本法则及一些导数公式，借助这些法则和求导公式，将方便地求出一些函数的导数.一、导数的四则运算法则定理3 设函数u=u（x）和v=v（x）在点x处都可导，则它们的和、差、积、商（分母不为零）构成的函数在点x处也都可导，且有以下法则：以上法则都可
前面根据导数的定义，我们求出了一些简单函数的导数，对于一些复杂的函数，如果仍按导数的定义求导，不仅烦琐，有时甚至是不可能的.因此，本节中，将介绍求导数的几个基本法则及一些导数公式，借助这些法则和求导公式，将方便地求出一些函数的导数.
一、导数的四则运算法则
定理3 设函数u=u（x）和v=v（x）在点x处都可导，则它们的和、差、积、商（分母不为零）构成的函数在点x处也都可导，且有以下法则：
以上法则都可以用导数的定义和极限的运算法则来验证，请读者自行证明.法则（1）、（2）可推广到任意有限个可导函数的情形.
二、复合函数的求导法则
前面，利用导数的四则运算法则和求导公式，求出了大量简单函数的导数，那么，对于复合函数的导数应该怎样求呢？求导问题，关于此，我们有下面的法则.
定理4 若函数u=φ（x）在x处可导，而函数y=f（u）在u处可导，则复合函数y=f［φ（x）］在x处可导，且有
证明从略.
上述定理表明，复合函数的导数等于函数对中间变量的导数乘以中间变量对自变量的导数，此定理称为复合函数求导的链式法则.
此法则还可以推广到有限多个中间变量的情形.
注：复合函数求导运算熟练后，可不必再写出中间变量，而直接由外往里、逐层求导即可，但是一定要分清楚函数的复合过程.
例13 求函数y=tan x2的导数.
例14 某铁球受热后，以4 cm3/s的速度膨胀，当铁球的半径为2 cm时，求它的表面积增加的速度.
解 设铁球的体积为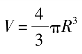
，球体的表面积为S=4πR2.
故它的表面积以4 cm2/s的速度在增加.
三、反函数的求导法则
设函数x=φ（y）在某一区间内是单调连续可导的，则它的反函数存在，且它的反函数y=f（x）在对应区间内也是单调连续，然而y=f（x）是否可导呢？如果可导，它们的导函数φ′（y）和f′（x）有什么关系呢？下面介绍反函数的求导法则.
定理5 如果函数x=φ（y）在某一区间内单调、可导，且φ′（y）≠0，则它的反函数y=f（x）在对应区间内单调、可导，且有(www.chuimin.cn)
也就是说，反函数的导数等于直接函数导数的倒数.
例15 求函数y=ax（a＞0且a≠1）的导数.
解 对数函数x=loga y在区间（0，+
）内单调、可导，且
所以，它的反函数y=ax在对应区间（-
，+
）内单调、可导，且
即
特别地，当a=e时，有（ex）′=ex.
例16 求函数y=arcsin x（-1＜x＜1）的导数.
解 函数x=sin y的反函数为y=arcsin x（-1＜x＜1）
因为x=sin y在区间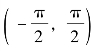
内单调、可导，且
所以，它的反函数y=arcsin x在对应区间（-1，1）内单调、可导，且
四、基本初等函数的求导公式
基本初等函数的求导公式，在初等数学的求导运算中起着重要作用，为了方便查阅，把基本初等函数的求导公式归纳如下：
习题2-6-2
1.选择题
2.求下列函数的导数：
3.加热一金属圆板，其半径以0.01 cm/s的速度均匀增加，问：当半径为200 cm时，圆板面积的增加速度为多少？
有关数学与生活的文章
- 详细阅读
-
高数上册：反函数、复合函数求导法则详细阅读
1）反函数的求导法则求导法则Ⅱ设y＝f（x）在区间Ix内单调、可导，且f′（x）≠0，则其函数x＝φ（y）在相应的区间Iy内也单调、可导，且证设函数的y＝f（x）的反函数x＝φ（y）的自变量y的增量为Δy，则相应地x的增量为Δx.由函数可导必连续的性质及反函数的连续性可得，x＝φ（y）在区间Iy内单调、连续，因此当Δy→0时，有Δx→0.且当Δy≠0时，有Δx≠0，则y，y＋Δy∈Iy，设Δy......
2023-11-19
-
函数连续性-数学与生活详细阅读
解 由于f=1，且因此函数f在点x0=0处右连续但不左连续，所以函数f在x0=0处不连续.例4 设函数讨论f在x=1处的连续性.解 由于f=2，且因此函数f在x=1处左连续且右连续，所以函数f在x=1处连续.例5 设函数问：a为何值时，函数y=f在点x=0处连续？......
2023-11-20
-
导数运算法则和复合函数求导详细阅读
一、导数的四则运算法则法则1：两个可导函数的和（差）的导数等于这两个函数的导数的和（差）.用公式可写为：（u±v）′=u′±v′.其中u、v为可导函数.法则2：在求一个常数与一个可导函数的乘积的导数时，常数因子可以提到求导记号外面去.用公式可写为：（cu）′=cu′.法则3：两个可导函数乘积的导数等于第一个因子的导数乘第二个因子，加上第一个因子乘第二个因子的导数.用公式可写为：（uv）′=u′v+......
2023-11-20
-
高等数学基础：隐函数求导公式详细阅读
【知识点回顾】一般而言，如果x与y的函数关系隐含在方程F（x，y）=0中，即x在某一区间取值时，相应地有确定的y值和其唯一对应，则称方程F（x，y）=0所确定的函数为隐函数.隐函数求导步骤：（1）方程两边对x进行求导；（2）在求导过程中把y看成x的函数y=f（x），用复合函数求导法则进行.一、二元函数的情形在第二章第六节中已经提出了隐函数的概念，并且指出了不经过显化直接由方程求它所确定的隐函数的方......
2023-11-20
-
高等数学上册：连续函数运算法则详细阅读
1）连续函数的四则运算法则函数的连续性是由函数的极限来定义的，所以根据极限的四则运算法则，可得下面的连续函数的四则运算法则.定理1若函数f（x）与g（x）都在点x0处连续，则函数f（x）±g（x），f（x）·g（x）都在点x0处连续，若再增加条件g（x0）≠0，则也在点x0处连续.证设函数f（x），g（x）都在点x0处连续，所以由极限的加、减、乘运算法则，可得即f（x）±g（x），f（x）·g......
2023-11-19
-
高数基础：多元复合函数求导法详细阅读
在一元函数中，我们已经知道复合函数的求导公式在求导法中所起的重要作用，对于多元函数来说也是如此.下面我们来学习多元函数的复合函数的求导公式.我们先以二元函数为例，如下所述.一、全导数【知识点回顾】复合函数的求导规则：对于复合函数y=f[φ（x）]，设y=f（u），u=φ（x），其中u叫作中间变量.则复合函数求导用公式表示为：即两个可导函数复合而成的复合函数的导数等于函数对中间变量的导数乘上中间变量......
2023-11-20
-
递归函数，求解阶乘，递归调用，数学函数详细阅读
在某些问题中，可以用调用函数自身的方式来解决问题。在一个函数中直接或间接地调用该函数自身的方式称做函数的递归调用。递归的概念在我们的自然生活中并不陌生。讲的故事又是其自身，这就相当于递归。这也是递归的例子。在数学中，更是有许多函数采用递归的定义形式。=3628800函数fact（）包含了对其自身的调用，因此fact（）是一个递归函数。来看一看这个递归函数的执行过程。图5.6递归求解3！......
2023-11-18
相关推荐