由于流体的速度与加速度是描述流体运动的两个主要运动参数，这里对它们做重点说明。流体加速度的计算公式代表的物理意义因而为“流体流动的加速度＝当地加速度＋对流加速度”。有人常误以为如果流体流动为稳态流动，则流体的加速度就一定为 0，这是一个错误的。假设空气的流动过程为稳态流动，且气流的流速可以表示为求空气气流的加速。......
2023-06-29
汽车油耗与行驶速度的最优关系
【摘要】：案例3 统计表明，某种型号的汽车在匀速行驶中每小时的油耗量y关于行驶速度v的函数关系可以表示为：y=+8.已知甲乙两地相距100 km，当汽车以多大的速度匀速行驶时，从甲地到乙地的油耗是最少的？学完本章内容，你再回过头来认真思考一下这些案例用到了哪些导数知识，你能解决这些实际案例中的问题吗？
本节之后将主要研究导数和微分的概念及其运算法则.导数与微分是一元函数微分学的两个基本概念.导数，从本质上看，是一类特殊形式的极限，是对函数变化率的度量，也是刻画函数相对于自变量变化快慢程度的数学抽象.微分，是函数增量的线性主部，它是函数增量的近似表示.微分与导数密切相关，它们都有着广泛的实际应用，和我们的生活密切相关的应用很多，比如下面的三个现实的案例.
案例1 路段限速为100 km/h，交警手持测速设备在距公路垂直距离为30 m的地方对过往车辆测速.一辆汽车在该公路上行驶，测速设备探得该汽车现距离交警50 m，以90 km/h的速度接近交警，请问：该车是否正在超速行驶？
案例2 汽车在限速为80 km/h的路段上行驶，在途中发生了事故，警察到现场后，测得该车的刹车痕迹长为30 m，而该车型的满刹车时的加速度为a=-15 m/s2，于是警察判该车为超速行驶，承担一部分责任，你知道为什么吗？(www.chuimin.cn)
案例3 统计表明，某种型号的汽车在匀速行驶中每小时的油耗量y（L）关于行驶速度v（km/h）的函数关系可以表示为：y=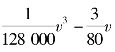
+8（0≤v≤120）.已知甲乙两地相距100 km，当汽车以多大的速度匀速行驶时，从甲地到乙地的油耗是最少的？最少油耗是多少？
学完本章内容，你再回过头来认真思考一下这些案例用到了哪些导数知识，你能解决这些实际案例中的问题吗？
有关数学与生活的文章
- 详细阅读
-
生成关系曲线：速度、加速度与位移的探究详细阅读
本章讲述如何生成关系曲线,即速度对时间的曲线、加速度对时间的曲线、位移对时间的曲线,或者是速度、角速度、位移等相互之间的关系曲线。打开第二章生成的螺纹传动,装配图的模型如图19-1所示。双击“Mechanism.1＼KINTime”直接进入栏内。图19-5 对话框图19-6 对话框生成速度、加速度等关系曲线选择对话框内的选项,出现对话框,如图19-7所示。......
2023-07-01
-
车辆行驶速度规定及漫水道路行驶注意事项详细阅读
第三十五条机动车遇道路宽阔、空闲、视线良好,在保证交通安全的原则下,最高时速规定如下:(一)小型客车在设有中心双实线、中心分隔带、机动车道与非机动车道分隔设施的道路上,城市街道为七十公里,公路为八十公里;在其他道路上,城市街道为六十公里,公路为七十公里。第四十六条车辆行经漫水路或漫水桥时,必须停车察明水情,确认安全后,低速通过。......
2023-10-29
-
汽车行驶系统总体结构认识详细阅读
车身承受了各种载荷，称为承载式车身。车桥是用来安装和支撑车轮的部件，并通过悬架与车架连接。图6.1汽车行驶系统的组成图6.2承载式车身结构图任务实施实施要求任务目标与要求①小组成员分工协作，利用汽车维修手册及实训资料，依据任务工作单制订工作计划，并通过小组自评或互评检查工作计划。②认识汽车行驶系统的整体结构，识别各机构及系统的组成，确定主要部件安装位置。......
2023-08-19
-
OSPF协议：计算网络最优路径，收敛速度快，详细阅读
OSPF 使用Dijkstra 的SPF 算法，对全网拓扑作出精确判断，并计算出无环路的最优路径。OSPF 使用IP 上层协议号89，有自身的可靠传输机制。OSPF 对网络整体把握，收敛速度快，适用于大型网络。运行OSPF 的路由器，通过互相发送hello 包建立邻居关系。DR 和BDR 在OSPF 域内的任何网段中只能有一个。DR、BDR 的选举进一步体现了OSPF 分级理念的精准控制和严格管理。......
2023-11-19
-
汽车行驶平稳性检测成果详细阅读
测试前需在被测轮胎侧面任意处贴装白色反光标志，为使光电组件正常工作，胎侧距光电二极管不得超过5 cm，检测程序分3 次进行。② 检查轮胎气压，视情况充至规定值。⑥ 将前桥置于左、右检测板上，尽量使车轮在检测板上居中停放。检测前应将侧倾试验台调整到台面处于水平状态。......
2023-10-11
-
声速测量实验：声波传播速度与气体状态关系详细阅读
了解声波在空气中传播速度与气体状态参量的关系。产生和接收超声波是用超声波传感器，其中的压电陶瓷晶片是传感器的核心，声速测量仪的发射器和接收器都是超声波传感器。在0℃时，声速v0=331.45m/s，显然在t℃时声速的理论计算式应为声速测量仪、示波器、信号发生器、温度计（公用）、导线若干。图14-2声速测量仪示意图 开启示波器和信号发生器。计算本实验测量的不确定度及百分误差。......
2023-11-02
-
测量速度和加速度的方法详细阅读
测量运动物体速度和加速度单击工具栏内的速度和加速度图标,出现对话框,如图20-1所示。图20-1 对话框图20-2 选择螺栓零件作为参考产品图20-3 选择螺母零件上的一个点图20-4 对话框更新显示用规则模拟运动关系单击工具栏内的使用法则曲线模拟图标,出现一个对话框,如图20-5所示。单击对话框内的选项卡,在栏内选择,选择后两个参数的状态由改为。图20-8 选项卡下显示的内容随模拟进程更新图20-9 速度和加速度随时间变化的曲线图20-10 对话框......
2023-07-01
相关推荐