连续复利与重要极限：数学与生活中的成果

2023-11-20 理论教育版权反馈

【摘要】：单利与复利的情况在银行储蓄中普遍存在.但是在证券市场这种较大波动的环境中，用年或者月份来计算利息或收益都会有明显的不合适.其原因是，在这些环境中结转次数非常多，比如今天投资的a股可能明天就会全部抛售转而投资b股.那么在结转期非常短的情况下，利滚利的复利会是一个什么情况呢？

单利与复利的情况在银行储蓄中普遍存在.但是在证券市场这种较大波动的环境中，用年或者月份来计算利息或收益都会有明显的不合适.其原因是，在这些环境中结转次数非常多，比如今天投资的a股可能明天就会全部抛售转而投资b股.那么在结转期非常短的情况下，利滚利的复利会是一个什么情况呢？

一、连续复利

连续复利是指在期数趋于无限大的极限情况下得到的利率，此时每一个时期都很短，可以看作无穷小量.复利在前面我们已经了解过了，就是复合利息，指的是收益还可以再产生收益，简单来说就是利滚利.

定义1 在某些情况下，现值在无限短的时间内按照复利计息，称为连续复利（Continuous Compounding）.

下面将讨论连续复利的终值计算方式：

例1 以上一节例2为基础，前面得到了应用复利计算方式，现值10 000元，年利率5%的情况下，3年后的终值为FV3=10 000×（1+0.05）3=11 576.25.

现在将计息次数从每年一次分为每月计算一次，那么对应的年利率也应该对应分解为月利率.这里考虑一种最简单的情况，即年利息直接分为12份得到月利息的情况.那么例4中三年后的终值变化为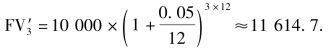 pagenumber_ebook=35,pagenumber_book=28

这个是按每月复利计息的一个结果，是不是和前面例4的结果不同了呢？

例2 如果是按更短的时间计息呢？比如每日、每时、每分、每秒.

按更短的时间计息，计息期数对应地就会更多，比如我们现在把一年分为t期计息，t具有t→+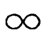 pagenumber_ebook=36,pagenumber_book=29 的一个趋势.列式可得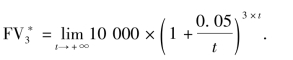

观察可见，这个式子中的利息部分是一个（1+0）的一个形式，它的计算与极限中的一个重要极限密切相关.

二、一个重要极限

下面给出极限中的一个重要极限： pagenumber_ebook=36,pagenumber_book=29 ，其中，e指的是自然常数，是一个无限不循环小数，其值约为2.718.这个重要极限的公式此处不加以证明，可以作为一般公式使用.其中的x也可以替换为其他的自变量.下面给出几个该公式的应用例子.

例3 求下列极限：

三、连续复利的结果(www.chuimin.cn)

通过前面介绍的重要极限的学习，我们就可以计算例5中连续复利的结果.

例5 以例1为基础，该模型中连续复利的式子为 pagenumber_ebook=36,pagenumber_book=29 现在我们计算其结果：

以复利的计算公式（FVn=PV×（1+i）n）为基础，假设我们每年分为t期计息，那么n年后连续复利的终值应为

也就是说，n年后连续复利的终值为FVn=PV×ein.

例6 一笔200 000元的资金，在进行一项年利率为8%的投资中，若是以连续复利的形式计算，5年后的终值是多少？

另外，下面几个图也说明了普通的复利与连续复利的关系.以1元为现值，以25%为年利率，分别计算5年内按年度复利、半年度复利以及连续复利的情况.可以看到计算复利越频繁，最后累计的金额就会越大，因为利息产生利息更频繁.

以上，我们讨论了货币的时间价值的三类典型模型，希望有助于读者收获更多生活中经济数学的知识.但经济数学及货币的时间价值的体现不局限于以上几类情况，希望读者可以从生活中慢慢体会及仔细品味.

课程思政：

从上面所学的内容可以看到，持续不断地在原有基础上进步，是飞速发展的一种方式.而且，进步时间间隔越短，进步速度越快.因此，要惜时如金，若能抓住每一个瞬间提高自己，必将极快地提升自己，实现自我的飞速发展.正如我们国家今时今日的发展成就，正是来自于无数国人争分夺秒的埋头苦干.

习题2-5

1.请计算下列极限：

2.请讨论：一笔50 000元的资金，在进行一项年利率为10%的投资中，若是以连续复利的形式计算，5年后的终值是多少？

3.请讨论在货币的时间价值中，计息方式的不同对于投资或者贷款的影响.