函数连续性-数学与生活

2023-11-20 理论教育版权反馈

【摘要】：解由于f=1，且因此函数f在点x0=0处右连续但不左连续，所以函数f在x0=0处不连续.例4 设函数讨论f在x=1处的连续性.解由于f=2，且因此函数f在x=1处左连续且右连续，所以函数f在x=1处连续.例5 设函数问：a为何值时，函数y=f在点x=0处连续？

自然界中有许多现象，如物体的运动、气温的变化、河水的流动、植物的生长等都是连续变化着的.这种现象在函数关系上的反映，就是函数的连续性.如运动着的质点，其位移s是时间t的函数，时间产生一微小的改变时，质点也将移动微小的距离（从其运动轨迹来看是一段连绵不断的曲线），函数的这种特征我们称之为函数的连续性，与连续相对立的一个概念，我们称之为间断.下面我们将利用极限来严格表述连续性这个概念以及连续性的相关数学问题.

一、函数的连续与间断

定义1 设函数f（x）在x0的某邻域U（x0）内有定义，且有

则称函数f（x）在点x0连续，x0称为函数f（x）的连续点.

由定义可知，函数f（x）在点x0连续，必须具备下列条件：

（1）f（x）在点x0有定义，即f（x0）存在；

（2）极限存在；

（3）=f（x0）.

以上三条，任意一条不满足，则函数f（x）在点x0处间断.

若函数y=f（x）在区间（a，b）内任一点均连续，则称函数y=f（x）在区间（a，b）内连续，称函数f（x）为区间（a，b）内的连续函数.若函数y=f（x）不仅在（a，b）内连续，且在a点右连续，在b点左连续，则称f（x）在闭区间［a，b］上连续，称函数f（x）为闭区间［a，b］内的连续函数.

例1 证明函数f（x）=3x2-1在x=1处连续.

证因为f（1）=2，且

故函数f（x）=3x2-1在x=1处连续.

例2 证明函数y=f（x）=在x=0处连续.

证 y=f（x）=在x=0的邻域内有定义，且f（0）=0，

从而=0=f（0），因此函数y=f（x）在x=0处连续.

我们曾讨论过x→x0时函数的左、右极限，对于函数的连续性可作类似的讨论.

定义2 设函数f（x）在点x0及某个左（右）半邻域内有定义，且有

则称函数f（x）在点x0是左（右）连续的.

函数在点x0的左、右连续性统称为函数的单侧连续性.

由函数的极限与其左、右极限的关系，容易得到函数的连续性与其左、右连续性的关系.

定理1 f（x）在点x0连续的充要条件：f（x）在点x0处既是左连续又是右连续.

例3 设函数

试问：在x0=0处函数f（x）是否连续？

解由于f（0）=1，且

因此函数f（x）在点x0=0处右连续但不左连续，所以函数f（x）在x0=0处不连续.

例4 设函数

讨论f（x）在x=1处的连续性.

解由于f（1）=2，且

因此函数f（x）在x=1处左连续且右连续，所以函数f（x）在x=1处连续.

例5 设函数

问：a为何值时，函数y=f（x）在点x=0处连续？

解因为f（0）=3，且

因此，当a=3时，y=f（x）在点x=0处连续.

在工程技术中，常用增量来描述变量的改变量.

设变量u从它的一个初值u1变到终值u2，终值u2与初值u1的差u2-u1称为变量u的增量，记为Δu，即

变量的增量Δu可能为正，可能为负，还可能为零.

设函数y=f（x）在x0的某个邻域U（x0）内有定义，若x∈U（x0），则(www.chuimin.cn)

Δx称为自变量x在点x0处的增量.显然，x=x0+Δx，此时，函数值相应地由f（x0）变到f（x），于是

称为函数f（x）在点x0处相应于自变量增量Δx的增量.

函数f（x）在点x0处的连续性，可等价地通过函数的增量与自变量的增量关系来描述.

定义3 设函数f（x）在x0的某个邻域内有定义，如果

则称函数f（x）在点x0处连续.

函数f（x）在x0处的单侧连续性，可完全类似地用增量形式描述.

二、连续函数的基本性质

定理2（连续函数的局部保号性）若函数y=f（x）在点x0处连续，且f（x0）＞0（或f（x0）＜0），则存在x0的某个邻域U（x0），使得当x∈U（x0）时有f（x）＞0（或f（x）＜0）.

定理3 若函数f（x），g（x）均在点x0处连续，则

（1）af（x）+bg（x）（a，b为常数）；

（2）f（x）g（x）；

（3） pagenumber_ebook=30,pagenumber_book=23

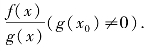
均在点x0处连续.

定理4（连续函数的反函数的连续性）若函数f（x）是在区间（a，b）内单调的连续函数，则其反函数x=f-1（y）是在相应区间（α，β）内单调的连续函数，其中α=min｛f（a+），f（b-）｝，β=max｛f（a+），f（b-）｝.

定理5（复合函数的连续性）设y=f［φ（x）］（x∈I）是由函数y=f（u），u=φ（x）复合而成的复合函数，如果u=φ（x）在点x0∈I连续，又y=f（u）在相应点u0=φ（x0）处连续，则y=f［φ（x）］在点x0处连续.

定理6 初等函数的连续性：

（1）基本初等函数在其定义域内连续；

（2）一切初等函数在其定义区间内连续.

例6 试求函数y=的间断点.

解因为函数是初等函数，所以其在定义区间（- pagenumber_ebook=30,pagenumber_book=23 ，-1），（-1，1），（1，+）内均连续，间断点即为函数无意义的点，所以，该函数的间断点是x=±1.

三、闭区间上连续函数的性质

1.根的存在定理（零点存在定理）

定理7 若函数y=f（x）在闭区间［a，b］上连续，且f（a）·f（b）＜0，则至少存在一点x0∈（a，b），使f（x0）=0.

例7 证明x3-4x2+1=0在区间（0，1）内至少有一个根.

解令f（x）=x3-4x2+1，则f（x）在[0，]1上连续，又f（0）=1＞0，f（1）=-2＜0，由零点定理知∃ξ∈（a，b），使f（ξ）=0，即ξ3-4ξ2+1=0，

所以方程x3-4x2+1=0在区间（0，1）内至少有一个根ξ.

2.介值定理

定理8 设函数y=f（x）为闭区间［a，b］上的连续函数，f（a）≠f（b），则对介于f（a）与f（b）之间的任一值c，至少存在一点x0∈（a，b），使f（x0）=c.

3.最大最小值定理

我们首先引入最大值和最小值的概念.

定义4 设函数y=f（x）在区间I上有定义，如果存在点x0∈I，使得对任意的x∈I，有

则称f（x0）为函数y=f（x）在区间I上的最大（小）值.最大值和最小值统称为最值.

定理9 （闭区间上连续函数的最值定理）若函数y=f（x）为［a，b］上的连续函数，则它一定在闭区间［a，b］上取得最大值和最小值.

课程思政：

通过对连续性这个知识点的学习，我们明白一个道理，无论做任何事情都要持之以恒，持续不断，一步一步地接近目标，不能急于求成、拔苗助长.

习题2-2

1.判断下列函数在点x=0处是否连续：

函数连续性-数学与生活

相关推荐