解读二手车买卖中的概率-数学与生活

2023-11-20 理论教育版权反馈

【摘要】：解设A=｛任取一只灯泡是次品｝；B1=｛任取一只为甲厂产品｝；B2=｛任取一只为乙厂产品｝；B3=｛任取一只为丙厂产品｝.由表可见，事件B1，B2，B3互斥，且B1+B2+B3=U，即B1，B2，B3构成一个完备事件组，则根据全概率公式有例3 100张彩票中有7张有奖彩票，甲先乙后各购买1张彩票，问：甲、乙中奖的概率是否相同？

人们总是希望能从已知的简单事件的概率中推算出未知的复杂事件的概率.为了达到这一目的，我们可以把一个复杂事件分解为若干个互斥的简单事件，再通过这些简单事件的概率计算，利用概率的加法公式和乘法公式得到最后结果.

想象一下你在一座拥堵的城市买了一辆二手车.你知道大约5%的二手车都被水泡过，而在被水泡过的车中大约80%以后都会出现严重的发动机问题；而没有被水泡过的车大约只有10%才会有严重的发动机问题.当然，没有任何二手车经销商会坦白地告诉你这辆二手车是不是被水泡过，所以你就必须求助于概率了.

你也许认为这个问题是一个比例问题.每卖出1 000辆车，有50辆之前被水泡过，其中80%即40辆之后会有问题.剩下的950辆没被泡过的车，我们预计10%即95辆也会发生同样的问题.因此，我们算出在1 000辆车中有40+95=135（辆）车在今后会有问题，得到的概率是13.5%.

如果你用这样的方法来解决问题，那么恭喜你了，你无形中用到了全概率法则.这也是概率问题经常使用的法则.

一、概率法则

1.概率加法公式

如果把两个事件A、B同时发生所组成的事件，称为A与B的积事件，记作AB.那么对于任意两个事件A、B，不论A、B是否互斥，都有下面的公式：

以上公式中的P（AB）又应该怎样来求呢？这就要用到下面的知识了.

2.条件概率与概率乘法公式

在实际问题中，除了研究事件A发生的概率P（A）外，往往还要研究“在事件B已经发生”的条件下，事件A发生的概率.一般说来，两者的概率不一定相同.为了区别起见，我们把后者称为条件概率，记作P（A/B）.

例如，从一副扑克牌（52张）中任意抽出一张，设A=“任取一张是红桃”，B=“任取一张有人头像”，则由古典概型可知，P（A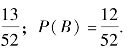）= pagenumber_ebook=20,pagenumber_book=13

假定我们要求的是在红桃牌中抽得一张“有人头像”的概率，即在事件A发生的条件下，事件B发生的条件概率，这时，基本事件是13张红桃牌，其中有人头像的牌只有3张.于是所要求的概率为P（B/A）=

那么，两个事件同时发生的概率，等于其中一个事件发生的概率与另一个事件在前一个事件已经发生的条件下的条件概率的积：

3.全概率公式

如果事件A1，A2，…，An互斥，P（Ai）＞0（i=1，2，…，n），且A1+A2+…+An=U（必然事件），我们称这样的一组事件为完备事件组，则对于任意事件B，都有

全概率公式的特殊情况对于任意两个事件A，B都有

例1 如果用全概率公式对上面二手车买卖的解法进行重新演绎，那么得到的算法是：

解设A=“二手车的发动机出现问题”；

B1=“被水泡过的二手车”；

B2=“没有被水泡过的二手车”.

则所求的概率为P（A）.

由表可见，事件B1，B2互斥，且B1+B2=U（必然事件），即B1，B2构成一个完备事件组，则根据全概率公式有(www.chuimin.cn)

例2 某仓库有一批外形相同的灯泡，其中50%的灯泡是甲厂生产的，次品率是1%；30%是乙厂生产的，次品率是2%；20%是丙厂生产的，次品率是0.5%，在这些灯泡中任取一只，取到次品的概率是多少呢？

解设A=｛任取一只灯泡是次品｝；

B1=｛任取一只为甲厂产品｝；

B2=｛任取一只为乙厂产品｝；

B3=｛任取一只为丙厂产品｝.

由表可见，事件B1，B2，B3互斥，且B1+B2+B3=U（必然事件），即B1，B2，B3构成一个完备事件组，则根据全概率公式有

例3 100张彩票中有7张有奖彩票，甲先乙后各购买1张彩票，问：甲、乙中奖的概率是否相同？

解设A=｛甲中奖｝，则A=｛甲不中奖｝；

B=｛乙中奖｝.

那么，根据古典概型有P（A）=

由于事件A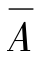， pagenumber_ebook=21,pagenumber_book=14 构成最简单的完备事件组，从而对于事件B，有

这是容易理解的，注意到乙购买彩票是在甲购买彩票之后，从而乙中奖包括甲中奖乙中奖与甲不中奖乙中奖两种情况，即事件B发生意味着积事件AB发生或积事件 pagenumber_ebook=21,pagenumber_book=14 发生，于是事件B当然等于积事件AB与积事件的和事件.同时注意到甲无论中奖与否，都不把所购买彩票放回，从而乙是从剩余99张彩票中购买1张彩票.根据全概率公式的特殊情况，有