数学与生活：成功学概率

2023-11-20 理论教育版权反馈

【摘要】：解法一设Ai=｛第i次射击命中目标｝，B=｛至少有一次命中目标｝=A1∪A2∪A3解法二用二项分布求解例3 某大学的社会学老教授给学生出了这样一道题目：如果一件事情成功的概率是1%，那么反复尝试100次，至少成功一次的概率大约是多少？

我们都知道，无论做任何事情，只要专心致志地坚持，就一定会获得一个较高的成功率.本节简要地介绍一些与集合和概率论相关的知识，通过学习随机事件与概率的有关内容，发掘同学们感兴趣的故事点，培养大家数学学习的兴趣，为我们后续学习打下坚实的基础.

一、事件之间的关系与运算

1.事件之间的关系

（1）包含关系.

若事件B发生必然导致事件A发生，则称事件A包含事件B，记作A⊃B或B⊂A.

（2）相等关系.

若事件A所包含的基本事件与事件B所包含的基本事件完全相同，则称事件A与事件B相等，记作A=B.

（3）互斥关系.

若事件A与事件B不可能同时发生，则称事件A与事件B互斥，或称事件A与事件B互不相容.

2.事件之间的运算

（1）事件的和.

事件A与事件B中至少有一个发生的事件称为事件A与事件B的和（或并），记为A∪B或A+B.

（2）事件的积.

事件A与事件B同时发生的事件称为事件A与B的积（或交），记为AB或A∩B.

（3）对立事件.

如果事件A与事件B中必有一个事件且仅有一个事件发生，即AB=∅，A∪B=Ω，则称事件A与事件B互为对立（或逆）事件.A的对立事件记为=Ω-A.

3.事件运算的基本性质

二、随机事件的概率

1.概率的统计定义

在相同条件下进行的n次重复试验中，事件A发生的次数nA称为事件A的频数，比值称为事件A发生的频率，记为fn（A），即fn（A）=.

显然，频率具有以下性质：

（1）对任一事件A，0≤fn（A）≤1；

（2）fn（∅）=0，fn（Ω）=1.

2.事件的独立性

定理1 事件A与B相互独立的充分必要条件是P（AB）=P（A）P（B）.

定理2 若事件A，B相互独立，则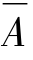 pagenumber_ebook=17,pagenumber_book=10 与B，A与也相互独立.

事件的独立性概念可以推广到任意有限多个事件的情形.例如，对于三个事件A1，A2，A3，如果有

则称事件A1，A2，A3两两独立，若同时还有

则称事件A1，A2，A3相互独立.

三、介绍两个重要的概率分布(www.chuimin.cn)

1.二项分布

一般地，在每次试验中，事件A或者发生或者不发生，若每次试验的结果与其他各次试验结果无关，同时在每次试验中，事件A发生的概率都为p（0＜p＜1），则称这样的n次独立重复试验为n重伯努里（Bernoulli）试验.

在n重伯努里试验中，事件A发生的次数X是一个离散型随机变量，它服从二项分布

简记为

说明：（1）n和p为二项分布中的两个参数，n是在相同条件下进行独立试验的次数，p是在一次试验中事件A出现的概率，p必须是一个小于1的正数.

（2）当n=1时，二项分布就是两点分布.

2.泊松分布

设随机变量Xn（n=0，1，2，…）服从二项分布

其中，pn是与n有关的数，且=λ＞0，则对于每个非负整数k，有

说明：（1）当二项分布中的参数n充分大，p足够小时，二项分布可以近似地等于以λ=np为参数的泊松分布，即

（2）一般当n＞20，p≤0.05时，就可用上述公式进行计算.

例2 某人独立地向某目标射击，击中目标的可能性为0.6，他连续射击了3次，则他至少命中目标一次的可能性为多少？

解法一设Ai=｛第i次射击命中目标｝（i=1，2，3），

B=｛至少有一次命中目标｝=A1∪A2∪A3

解法二用二项分布求解

例3 （贵在坚持）某大学的社会学老教授给学生出了这样一道题目：如果一件事情成功的概率是1%，那么反复尝试100次，至少成功一次的概率大约是多少？

解法一用二项分布求解

设X=｛反复尝试100次，至少成功一次｝

解法二用泊松分布近似计算

设X=｛反复尝试100次，至少成功一次｝

该题中，经过进一步的计算可知，若这件事反复尝试200次，300次，…，直至500次的时候，成功的概率已达99%.

课程思政：

在生活中只要学会连续仔细地观察遇到的事情，就能寻找恰当的数学方法去解决它们，总结出持之以恒的可行策略，坚持下去就有较大成功的希望.在我们面对一件难事时，虽然总觉得无从下手或觉得成功的希望非常渺茫（1%的成功），但也要耐得住考验、经得起失败，既要坚信付出一定会有回报，更要坚信知识可以改变命运.

习题1-3

1.某班级小组有5人做游戏，每人实名写一个祝福纸条，把5个写好的纸条揉搓成团放在一起摇匀，然后每个人从中随机抽取一个，问：至少有一个人取回自己写的祝福纸条的概率是多少？

2.请判断：是谁在说谎？

如果我们已经知道某件事是甲、乙、丙、丁四人中某一个人干的，但是不知道是谁干的，于是询问四人后回答如下：（1）甲说是丙干的；（2）乙说我没有干；（3）丙说甲讲的不符合事实；（4）丁说是甲干的，若其中三人说的是对的，一人说的不对，那么是谁干的？

3.请问：游戏是否公平？

现有三张牌，一张牌两面都是点，一张牌两面都是圈，一张牌一面是点一面是圈，甲、乙两人做游戏：甲打乱牌后，随机抽出一张牌给乙看，如果乙看到一张牌上面是点，去猜牌的另一面，两面都一样算甲赢，否则算乙赢，问：游戏是否公平？

数学与生活：成功学概率

相关推荐