EtherCAT是一个可用于现场级的超高速I/O网络,它使用标准的以太网物理层和常规的以太网卡,传输介质可为双绞线或光纤。一般常规的工业以太网都是采用先接收通信帧,进行分析后作为数据送入网络中各个模块的通信方式,而EtherCAT的以太网协议帧中已经包含了网络中各个模块的数据。EtherCAT技术已经完成,专门的ASIC芯片也在实现之中。目前市场上已提供了从站控制器,EtherCAT的规范也成为了IEC/PAS文件。图1-19 EtherCAT通信协议模型......
2023-11-20
电力系统波形畸变是由非线性用电设备产生的,畸变波形可以用一组正弦波形叠加综合来近似表示。畸变的波形仍然是周期性波形,理论上任何周期性波形都能分解成傅里叶级数,称为谐波分析或频域分析。谐波分析是计算周期性畸变波形基波、谐波幅值和相角的基本方法。
傅里叶级数是一种研究和分析谐波畸变的有效方法。通过傅里叶分解能够对畸变波形的各种分量进行检测。将采样取得的N个离散信号通过离散傅里叶变换,可以得到各次谐波分量的频谱,由此可以计算出电流、电压有效值及其相应的总谐波畸变率、功率等各种电力参数。
离散傅里叶变换的公式如下:
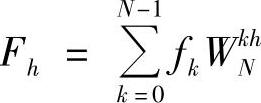
式中,fk为第k个时刻的采样值。
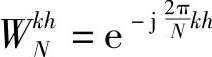
式中,k=0,1,2,…,N-1;h=0,1,2,…,N-1。
按照上式作离散傅里叶变换,计算量会随着采样点N的增大而剧增。目前普遍采用的算法是改进的快速傅里叶变换算法。对于采样点为N的快速傅里叶变换,只需计算N·log2N次复加和复乘,而离散傅里叶变换则需要N2次复乘和N(N-1)次复加。因此,采用快速傅里叶变换算法,既能完成对谐波的分析,又能达到实时处理的效果。
本文采用一种基-2算法,该方法把N取为2的整数次幂。即N=2m,m为正整数。设采样次数为128,即N=128=27,m=7。
下面用一个N=8的情况来说明FFT的基本思路。
FFT程序一般分为倒序和递推运算两部分。
倒序是指将N个自然编号的十进制数按照其编号的二进制码的倒序重新排列这些数据。比如编号为0和4的数,其二进制码分别为000b和100b,倒序后为000b和001b,那么新的序列中,它们的编号变为0和1。将N个数倒序排列的步骤如下:
第一步:将N(N=2m,m为整数)个自然编号的十进制数每隔一个挑出来,分成两组依次排列。(www.chuimin.cn)
第二步:再将每组的十进制数分别每隔一个挑出来,再分别分为两组依次排列。如此重复下去,共进行m-1步(共分成 组)即可完成。
组)即可完成。
其中的规律如下:
将第n个数据的序号用L(n)表示,则有
L(0)=0 L(1)=N/2,
L(2M)=L(M)/2,M=0,1,2,…
L(2M+1)=L(2M)+N/2,M=0,1,2,…
快速傅里叶变换是一种递推运算,它的基本计算因子是蝶形因子,如图9-8所示。
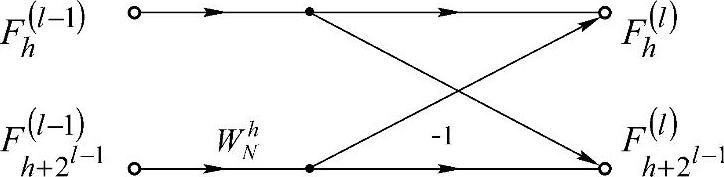
图9-8 蝶形算式流图
只要能够推导出蝶形因子中的各个系数表达式,就可以采取循环的方式编程。
快速傅里叶变换实际是一种递推运算,可以通过循环编程的方法来实现。循环编程的重点首先是要确定蝶形因子算式中各个参数的表达式,然后要计划好用几重循环,每个循环的循环次数如何表达。
有关现场总线与工业以太网及其应用技术的文章

EtherCAT是一个可用于现场级的超高速I/O网络,它使用标准的以太网物理层和常规的以太网卡,传输介质可为双绞线或光纤。一般常规的工业以太网都是采用先接收通信帧,进行分析后作为数据送入网络中各个模块的通信方式,而EtherCAT的以太网协议帧中已经包含了网络中各个模块的数据。EtherCAT技术已经完成,专门的ASIC芯片也在实现之中。目前市场上已提供了从站控制器,EtherCAT的规范也成为了IEC/PAS文件。图1-19 EtherCAT通信协议模型......
2023-11-20

Web并不是Intranet内的唯一设置,Intranet还需要采用其他一些公开标准,如SMTP及FTP服务器等。仅供单位内部使用Intranet大部分只供单位内部使用,不对外开放。为了使单位内部能从Internet上检索信息,又不让外界非法进入,通常采用防火墙将Intranet与Internet隔离。针对部门或整个企业一对多的信息交流,Intranet通过Web界面公布信息,减少大量的过时文件,减少生产印刷和传送企业信息的成本。Intranet可以及时地传送以下信息:产品种......
2023-11-20

节省硬件数量与投资由于现场总线系统中分散在设备前端的智能设备能直接执行多种传感、控制、报警和计算功能,因而可减少变送器的数量,不再需要单独的控制器、计算单元等,也不再需要DCS系统的信号调理、转换、隔离技术等功能单元及其复杂接线。......
2023-11-20

由于标准并未统一,所以对现场总线也有不同的定义。但现场总线的本质含义主要表现在以下6个方面。现场设备互连是基本的要求,只有实现互操作性,用户才能自由地集成FCS。通过网络对现场设备和功能块统一组态,把不同厂商的网络及设备融为一体,构成统一的FCS。......
2023-11-20

GND:14、28、44、52、83、86引脚,地。在RSTDRV引脚的下降沿,RTL8019AS检测SLOT16引脚的状态。图8-20 RTL8019AS引脚图3.存储器接口引脚BCSB:75引脚,BROM片选,低有效,读取BROM时使用。BD0~BD7:77~82、84、85引脚,IBROM数据总线。PL0、PL1:74、77引脚,选择网络介质类型。当RTL8019AS的介质类型为10Base2方式或自动检测方式连接测试失败时,该引脚为高;否则,该引脚为低。LED1、LED2:62、63引脚。......
2023-11-20

轮询连接是预定义主/从连接组中定义的4种I/O连接之一,轮询连接实例ID为2。轮询连接传送的是I/O轮询命令和轮询响应报文。从站返回的轮询响应信息由连接ID和I/O数据两部分组成。图7-20 轮询应用实例主站和从站轮询连接Produced_Connection_ID属性的值是由组报文、报文ID和从站的MAC ID共同决定的。......
2023-11-20

下面将要介绍的寄存器规定了ASIC硬件功能和报文处理过程。表5-8 方式寄存器1S和方式寄存器1R(续)2.状态寄存器状态寄存器反映SPC3当前的状态并且为只读,状态寄存器各位的定义见表5-9。中断控制器最多可存储16个中断事件。协议规定SPC3从最高的波特率开始查询。......
2023-11-20

看来,它成为过程控制领域中唯一的工业以太网标准已成定局。图1-15 工业以太网与相关现场总线协议的应用定位看起来,INONA和OPC基金会一直在试图缓和和调节这场潜在的标准之争。但这场工业以太网协议之争,并未因此停息。它属于设备层中的工业以太网协议,目前在Modicon的PLC中用得很多。目前以太网收发器的功耗较大,一般均在60mA以上。可见,目前基于以太网的现场仪表尚不能完全满足上述要求。......
2023-11-20
相关推荐