基金会现场总线,是在过程自动化领域得到广泛支持和具有良好发展前景的技术。屈于用户的压力,这两大集团于1994年9月合并,成立了现场总线基金会,致力于开发出国际上统一的现场总线协议。基金会现场总线分低速H1和高速H2两种通信速率。H1的传输速率为31.25 kbit/s,通信距离可达1900 m,可支持总线供电,支持本质安全防爆环境。H2总线标准也已形成。......
2023-11-22
差错控制的目的是使用一些方法发现差错并加以纠正。通常在信息码元的基础上增加一些冗余码元,冗余码元与信息码元之间存在一定的关系,传输时,将信息码元与冗余码元组成码组(码字)一起传输。
不同的码字长度影响了编码的差错检测能力。例如,一个事物有“有”、“无”两种状态,若用一位码元表示:“1”表示有,“0”表示无,在出现传输错误时,接收端无法发现;若用两位码元组成的码组表示:“11”表示有,“00”表示无,则接收端可发现一位错误;若用3位码元组成的码组表示:“111”表示有,“000”表示无,则接收端可发现一位错误和两位错误。如果考虑出现一位错的概率远大于出现两位错的概率,并认为两位错极少出现,则接收端可以对一位错进行纠错。两个等长码组之间对应位不同的数目称为这两个码组的海明距离,简称码距。一般来说,码距越大,编码的检错和纠错能力越强。但是随着冗余码的增加,传输效率将降低,而且过多的冗余码也增加了传输出现错误的可能性,因此,选择编码还应考虑信道的误码率。
根据对码组处理方式的不同,差错控制的方式基本上有两类:一类是在码组中带有足够的冗余信息,以便在接收后能够发现并自动纠正传输差错,简称纠错;另一类是在码组仅包含足以使接收端发现差错的冗余信息,靠重发保证正确传输,简称检错重发方式,这种方式实现比较简单。
无论是纠错方式,还是检错重发方式,都有很多具体的编码方法。由于篇幅的关系,这里仅介绍一种纠错码和一种检错码的编码实现方法。
1.海明码
(1)工作原理
海明码(Hamming)是一种简单实用的一位错纠错编码,它的码组长度、冗余校验位长度和码组中的最大数据位长度满足下列关系:
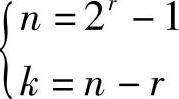
式中,n为码组位长度;r是冗余校验位长度;k是码组中的最大数据位长度。分析可知,冗余校验位长度越长,码组传输数据的效率越高。当数据长度不能满足上式的最大数据位长度值时,可以用固定的数据位填充。
在海明码的编码过程中,冗余码从左至右依次填充到2j(j=0,1,…,r-1)的位置上,码组中剩余位填充数据位,如图2-18所示。

图2-18 海明纠错码格式
图中,*表示数据码;P表示冗余校验数据码。
如果冗余码的位数为r,则存在这样一个(2r-1)行×r列的编码矩阵,矩阵元素等于0或1,并且每一行的元素所组成的二进制编码等于行数的二进制编码。对于海明纠错码,要求码组数据与这一矩阵相乘满足下列关系:

式中,*和P仍为数据码和校验码;b=1,b=0;l1=l2=…=lr-1=lr=0。根据这一关系可以计算出冗余校验码。这里矩阵的乘除运算与普通矩阵的乘除运算一样,加减运算为“异或”运算。
接收方收到数据后,将码组数据与发送方编码时用的编码矩阵相乘,若得到的行矩阵为零矩阵,说明传输正确;否则传输有错,且出错位是这一行的元素所组成的二进制数所对应的数据位。
(2)工作过程
下面以数据(信息)1101为例,给出海明码编码、译码及纠错的工作过程。
1)编码过程。
根据公式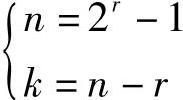 ,可选择数据长k=4,冗余码长r=3,码组长n=7。由关系式
,可选择数据长k=4,冗余码长r=3,码组长n=7。由关系式

可以计算出:P1=1
P2=0
P3=0
所求的海明编码为(1 0 1 0 1 0 1)。
2)译码过程。
假设接收方接收到的数据为(1 0 1 0 1 1 1),传输出错判断:(1 0 1 0(www.chuimin.cn)
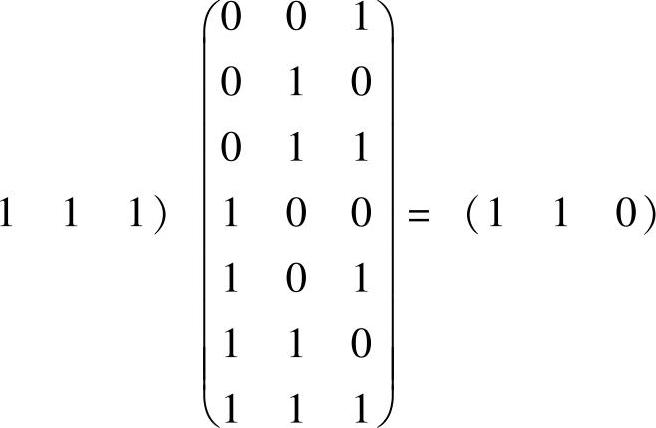
说明传输出错,(110)2=6,可以进一步判断出第6位出错。
3)纠错。
将接收到的编码左数第6位取反,恢复出正确数据。
(1010111)→(1010101)
2.循环冗余编码
(1)工作原理
循环冗余编码(CRC)的方法是将要发送的数据比特序列当做一个多项式f(x)的系数,在发送方用收发双方预先约定的生成多项式G(x)去除,得到一个余数多项式。将余数多项式加到数据多项式之后发送到接收端。接收端用同样的生成多项式G(x)去除接收数据多项式f(x),得到计算余数多项式。如果计算余数多项式与接收余数多项式相同,则表示传输无差错;如果计算余数多项式不等于接收余数多项式,则表示传输有差错,由发送方重发数据,直至正确为止。CRC检错能力强,实现容易,是目前应用最广泛的校验方法之一,其工作原理如图2-19所示。

图2-19 CRC基本工作原理
(2)工作过程
1)在发送端,发送数据多项式为f(x)xk,其中k为生成多项式的最高幂值。例如CRC-12的最高幂值为12,则发送f(x)x12。对于二进制乘法来说,f(x)x12的意义是将发送数据比特序列左移12位,用来存入余数。
2)将f(x)xk除生成多项式G(x),即

式中,R(x)为余数多项式。
3)将f(x)xk+R(x)作为整体,从发送端通过通信信道传送到接收端。
4)接收端对接收数据多项式f′(x)采用同样的运算,即
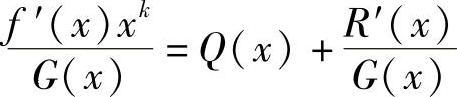
求得计算余数多项式。
5)接收端根据计算余数多项式R′(x)是否等于接收余数多项式R(x)来判断是否出现传输错误。实际的CRC校验码生成是采用二进制模二算法,即减法不借位,加法不进位,这是一种异或操作。
(3)CRC生成多项式
CRC列入国际标准的生成多项式有:
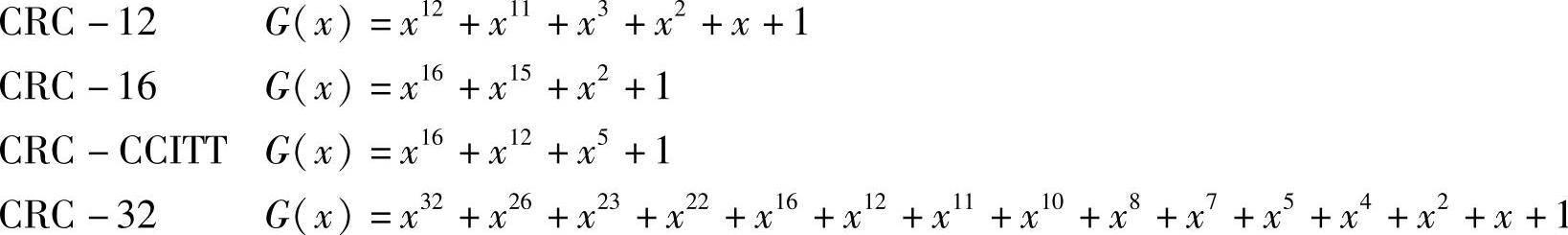
生成多项式的结构及检错效果是经过严格的数学分析与实验后确定的。
(4)CRC编码实例
假设发送数据位序列为111011,生成多项式位序列为11001。将发送位序列111011(f(x))乘以24得1110110000(f(x)xk),然后除生成多项式位序列11001(G(x)),不考虑借位,按模二运算,得余数位序列为1110(R(x))。
有关现场总线与工业以太网及其应用技术的文章

基金会现场总线,是在过程自动化领域得到广泛支持和具有良好发展前景的技术。屈于用户的压力,这两大集团于1994年9月合并,成立了现场总线基金会,致力于开发出国际上统一的现场总线协议。基金会现场总线分低速H1和高速H2两种通信速率。H1的传输速率为31.25 kbit/s,通信距离可达1900 m,可支持总线供电,支持本质安全防爆环境。H2总线标准也已形成。......
2023-11-22

INTERBUS定义了该模型的第1、2、7层。INTERBUS具有强大的可靠性、可诊断性和易维护性。INTERBUS采用了集总帧型的数据环通信。强大的诊断功能是INTERBUS区别于其他总线所独有的。INTERBUS CLUB负责向设备生产厂家提供INTERBUS的接口方案和接口芯片,向其成员提供信息,帮助解决技术问题及为特定的应用找寻合适的INTERBUS产品。INTERBUS的技术发起人为德国菲尼克斯公司。另外,在美国和中国也设有INTERBUS技术中心。......
2023-11-22

EtherCAT是由德国Beckhoff公司开发的,并且在2003年底成立了ETG工作组。EtherCAT是一个可用于现场级的超高速I/O网络,它使用标准的以太网物理层和常规的以太网卡,介质可为双绞线或光纤。图1-20 EtherCAT协议标准帧结构EtherCAT的通信协议模型如图1-21所示。图1-21 EtherCAT通信协议模型EtherCAT技术已经完成,专门的ASIC芯片也在实现之中。EtherCAT的规范也成为了IEC/PAS文件IEC/PAS 62407。......
2023-11-22

PCI总线是由Intel公司提出的。PCI总线不是由ANSI通过的标准,但由于它是由厂家自发制定执行的标准,具有众多的优点,拥护者,执行者众多,成了事实上的标准。PCI总线共有100个引脚,如果只作为目标设备,至少需要47条,如作为主设备则需要49条。本设计使用位命令字,其定义如下:3.PCI总线基本协议PCI上的基本总线传输机制是突发成组传输。......
2023-11-22

WorldFIP技术硬件体系由两个互补的部分组成:通信控制器和通信介质器件。5)用于WorldFIP连接的费用要求。WorldFIP现场总线第一个通信控制器是在1987年开发成功的。图8-9 WorldFIP现场总线通信站的连接......
2023-11-22

现场总线控制网络处于企业网络的底层,或者说,它是构成企业网络的基础。从图中可以看出,除现场的控制网络外,上面的ERP和MES都采用以太网。图中的ERP与MES功能层大多采用以太网技术构成数据网络,网络节点多为各种计算机及外设。控制网络的主要作用是为自动化系统传递数字信息。这些都需要在现场控制层内部,在FCS与MES、ERP各层之间,方便地实现数据传输与信息共享。......
2023-11-22

在ControlNet出现以前,没有一个网络在设备或信息层能有效地实现这样的功能要求。ControlNet是目前世界上增长最快的工业控制网络之一。ControlNet基于生产者/消费者这一先进的网络模型,提供了更高的有效性、一致性和柔韧性。所有的这些现实问题推动了ControlNet的开发和发展,它正是满足不同需要的一种实时的控制层的网络。ControlNet协议的制定参照了OSI的7层协议模型,并参照了其中的第1、2、3、4、7层。ControlNet中,网络层和传输层的任务是建立和维护连接。......
2023-11-20

OSI参考模型和TCP/IP参考模型有很多相似之处。TCP/IP参考模型最初没有明确区分服务、接口和协议,虽然后来人们试图改进它以便接近于OSI。因此,OSI模型中的协议比TCP/IP参考模型的协议具有更好的隐藏性,在技术发生变化时能相对比较容易地替换掉。OSI参考模型产生在协议发表之前。而TCP/IP却正好相反。现在我们从一般问题转向更具体一些,两个模型间明显的差别是层的数量:OSI模型有7层,而TCP/IP模型只有4层。......
2023-11-22
相关推荐