定积分及二重积分作为和的极限的概念，可以很自然地推广到三重积分.定义 设f是空间有界闭区域Ω上的有界函数，将Ω任意分成n个小区域Δv1，Δv2，…，Δvn，其中Δvi表示第i个小闭区域，也表示它的体积.在每个Δvi上任取一点，作乘积fΔvi（i=1，2，…......
2023-10-19
高等数学基础：三重积分计算法
【摘要】：二重积分的被积函数是一个二元函数，它的积分域是一平面区域.如果考虑三元函数f在一空间区域上的积分，就可得到三重积分的概念.一、三重积分概念设函数u=f在空间有界闭区域任意划分成n个子域ΔV1，ΔV2，ΔV3，…，ΔVn，它们的体积分别记作ΔVk（k=1，2，…
二重积分的被积函数是一个二元函数，它的积分域是一平面区域.如果考虑三元函数f（x，y，z）在一空间区域（V）上的积分，就可得到三重积分的概念.
一、三重积分概念
设函数u=f（x，y，z）在空间有界闭区域（V）任意划分成n个子域ΔV1，ΔV2，ΔV3，…，ΔVn，它们的体积分别记作ΔVk（k=1，2，…，n）.在每一个子域上任取一点（ξk，ηk，ζk），并作和数
如果不论ΔVk怎样划分，点（ξk，ηk，ζk）怎样选取，当n→+∞而且最大的子域直径δ→0时，这个和数的极限都存在，那么此极限就称为函数f（x，y，z）在域V上的三重积分，记作：
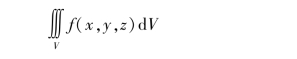
即
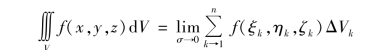
如果f（x，y，z）在域V上连续，那么此三重积分一定存在.
对于三重积分没有直观的几何意义，但它却有着各种不同的物理意义.
二、直角坐标系中三重积分的计算方法
这里我们直接给出三重积分的计算公式，具体它是怎样得来的，请大家参考相关书籍.
直角坐标系中三重积分的计算公式为：
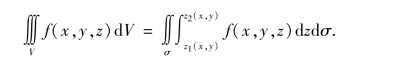
此公式是把一个三重积分转化为一个定积分与一个二重积分的问题，根据我们前面所学的结论即可求出.
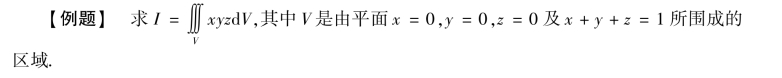
解：把I化为先对z积分，再对y和x积分的累次积分，那么应把V投影到xOy平面上，求出投影域σ，它就是平面x+y+z=1与xOy平面的交线和x轴、y轴所围成的三角区域.
我们为了确定出对z积分限，在（σ）固定点（x，y），通过此点作一条平行于z的直线，它与V上下边界的交点的竖坐标：z=0与z=1-x-y，这就是对z积分的下限与上限，于是由积分公式得：
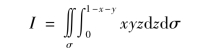
其中σ为平面区域：x≥0，y≥0，x+y≤1，如图9.12中阴影部分所示.
再将σ域上的二重积分化成先对y后对x的累次积分，得：
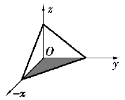
图9.11
三、柱面坐标系中三重积分的计算法
我们先来学习一下空间中的点用极坐标的表示方法.(www.chuimin.cn)
平面上点P可以用极坐标（ρ，θ）来确定，因此空间中的点P可用数组（ρ，θ，z）来表示.显然，空间的点P与数组（ρ，θ，z）之间的对应关系是一一对应关系，数组（ρ，θ，z）称为空间点P的柱面坐标.它与直角坐标的关系为：
构成柱面坐标系的3族坐标面分别为：
ρ=常数：以z轴为对称轴的同轴圆柱面族；
θ=常数：通过z轴的半平面族；
z=常数：与z轴垂直的平面族.
因此，每3个这样的坐标面确定着空间的唯一的一点，由于利用了圆柱面，所以称为柱面坐标.
柱面坐标系下三重积分的计算公式为：
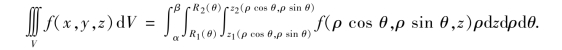
习题9.4
1.计算.
复习题九
一、填空题
1.设曲顶柱体z=x2y2，区域D：x2+y2≤4，则曲顶柱体的体积用二重积分表示为：____________________.
2.设曲顶柱体z=x+y，D：由y=2x，x轴，y轴所围成的区域，则曲顶柱体的体积用二重积分表示为：____________________.
二、选择题
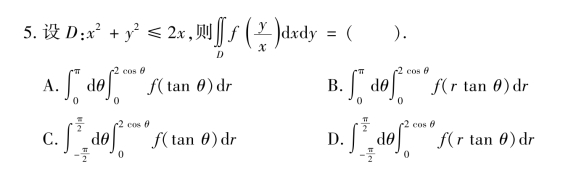
三、计算下列二重积分
中国现代数学先驱——陈省身
有关高等数学基础的文章
- 详细阅读
-
《高等数学基础》MATLAB：积分求解详细阅读
一、求积分求积分由函数int来实现.该函数的一般调用格式为：int（s）：没有指定积分变量和积分阶数时，系统按默认变量对被积函数或符号表达式s求不定积分.int（s，v）：以v为自变量，对被积函数或符号表达式s求不定积分.int（s，v，a，b）：求定积分运算.a，b分别表示定积分的下限和上限.该函数求被积函数在区间[a，b]上的定积分.a和b可以是两个具体的数，也可以是一个符号表达式，还可以是无......
2023-11-20
- 详细阅读
-
微积分基本公式-高等数学基础详细阅读
一、积分变上限函数设函数f（x）在区间[a，b]上连续，并且设x为[a，b]上的一点.则函数f（x）在部分区间[a，x]上的定积分∫xaf（x）dx存在且连续，为了区分积分变量，我们用t表示积分变量，记为定理1（微积分基本定理）如果函数f（x）在区间[a，b]上连续，则积分变上限函数在[a，b]上具有导数，并且它的导数为图5.8定理1表明，Φ（x）是连续函数f（x）的一个原函数，因此可得.定理2......
2023-11-20
-
高等数学基础：不定积分概念详细阅读
一、不定积分的概念原函数定义：设f（x）是定义某区间I上的已知函数，若存在一个函数F（x），对于该区间上每一点都满足：F′（x）=f（x）或dF（x）=f（x）dx，则称F（x）是f（x）在该区间I上的一个原函数.如已知f（x）=2x，由于F（x）=x2满足F′（x）=（x2）′=2x，所以F（x）=x2是f（x）=2x的一个原函数.同理，x2+1，x2-1，x2+10等也都是f（x）=2x的原函......
2023-11-20
- 详细阅读
-
高等数学基础：定积分换元法与分部积分法详细阅读
定积分的换元积分法和分部积分法，就是在以前学习的不定积分的第一类还原积分法（凑微分法）和第二类还原积分法及分部积分法的基础上来求定积分.下面就来讨论定积分的这两种计算方法.一、定积分的第一类换元积分法（凑微分法）【知识点回顾】第4章中不定积分第一类换元法（即凑微分法）主要介绍了下面6种代换：定积分第一类换元法（即凑微分法）关键就是求出不定积分，再代入上下限即可.下面举例来说明.解：如将（3x-2）......
2023-11-20
-
高等数学基础：定积分在几何上的应用详细阅读
一、定积分的元素法（微元法）在定积分的应用中，人们经常采用所谓的元素法，为此，回顾一下之前讨论过的曲边梯形的面积计算方法.设f在区间[a，b]上连续，且f≥0，求以曲线y=f为曲边，底为[a，b]的曲边梯形的面积A，如图5.9所示.图5.9（一）分割用任意一组分点a=x0＜x1＜…......
2023-11-20
相关推荐