一、空间直角坐标系在空间，使3条具有相同单位长度的数轴相互垂直且相交于一点O，这3条数轴分别称为x轴、y轴和z轴，一般是把x轴和y轴放置在水平面上，z轴垂直于水平面.z轴的正向按如图7.1所示的右手法则判断，具体规定如下：伸出右手，让四指与大拇指垂直，并使四指先指向x轴的正向，然后让四指沿握拳方向旋转90°指向y轴的正向，这时大拇指所指的方向就是z轴的正向.这样就组成了右手空间直角坐标系Oxyz.......
2023-11-20
直角坐标系下二重积分的计算-高等数学基础
【摘要】：二重积分直接不容易积分，须化为二次定积分来计算，设被积函数z=f（x，y）在D上连续，它是一个连续曲面，因此可将其都看作以D为底，曲面z=f（x，y）为顶的曲顶柱体的体积.在直角坐标系下，区域D可以看成由一系列小矩形区域构成，任取一小矩形区域Δσ，则它的边长为Δx，Δy，面积为Δσ=ΔxΔy，即dσ=dxdy，为求二重积分，必须对区域D进行划分，如图9.4所示，区域D加在x=a，x=b，y=y1（
二重积分直接不容易积分，须化为二次定积分来计算，设被积函数z=f（x，y）在D上连续，它是一个连续曲面，因此可将其都看作以D为底，曲面z=f（x，y）为顶的曲顶柱体的体积.
在直角坐标系下，区域D可以看成由一系列小矩形区域构成，任取一小矩形区域Δσ，则它的边长为Δx，Δy，面积为Δσ=ΔxΔy，即dσ=dxdy，
为求二重积分，必须对区域D进行划分，如图9.4所示，区域D加在x=a，x=b，y=y1（x），y=y2（x）4条曲线之间；如图9.5所示区域D加在y=c，y=d，x=φ1（x），x=φ2（x）4条曲线之间.
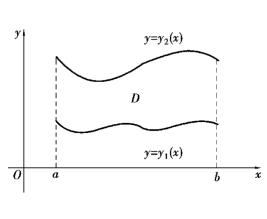
图9.4
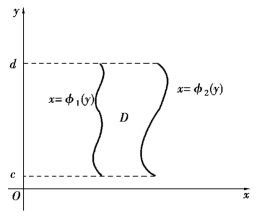
图9.5
对区域D进行划分后，要求二重积分，这里我们采取的方法是累次积分法.即将二重积分化为两个定积分.也就是先将x看成常量，对y进行积分，然后再对x进行积分，或者是先将y看成常量，对x进行积分，然后在对y进行积分.为此我们有积分公式，如下：
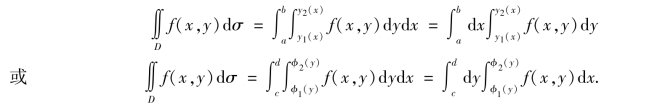
上下限都是常数的称为内积分，上下限不全都是常数的称为外积分，求二重积分是先求外积分，再求内积分.
注意：对含有x的变量进行积分时，将y看成常量，对含有y的变量进行积分时，将x看成常量.
(www.chuimin.cn)
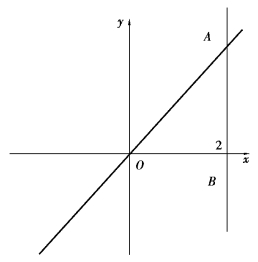
图9.6
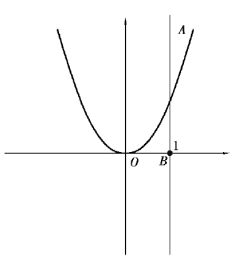
图9.7
【知识点回顾】
习题9.2
1.计算下列二重积分.
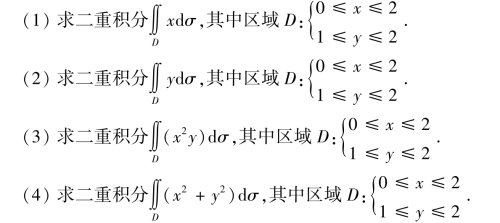
2.计算下列二重积分.
有关高等数学基础的文章
- 详细阅读
-
平面直角坐标系中的位似变换探讨详细阅读
在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点（x，y）对应的位似图形上的点的坐标为_________．1．在平面直角坐标系中，△ABC与△A′B′C′是以原点为位似中心的位似图形，若点A和它的对应点A′的坐标分别为（－4，2），（8，－4），则△ABC与△A′B′C′的相似比是（ ）．2．如图，△ABC和△A′B′C′位似，位似......
2023-07-03
-
高等数学基础：三重积分计算法详细阅读
二重积分的被积函数是一个二元函数，它的积分域是一平面区域.如果考虑三元函数f在一空间区域上的积分，就可得到三重积分的概念.一、三重积分概念设函数u=f在空间有界闭区域任意划分成n个子域ΔV1，ΔV2，ΔV3，…，ΔVn，它们的体积分别记作ΔVk（k=1，2，…......
2023-11-20
-
MATLAB简介|高等数学基础详细阅读
，xn，yn，选项n）画y=cosx的图像，并用蓝色，点画线，五角星标注.clearclcx=0：0.02：2*piy=cosplot·画y=x^3图像，用黑色、实线、星号表示.·clear·clcx=0：0.2：5·y=x.^3·plotholdon/off命令控制是保持原有图形还是刷新原有图形，不带参数的hold命令在两种状态之间进行切换.绘制分段函数程序如下：x=-10：0.1：0y=x.^2plot(x,y)holdonx=0：0.1：10y=x.^3plot(x,y)练习一1.谈谈你对MATLAB的认识.2.绘制y=sin2x在[0，2π]范围内的图像.3.绘制y=x3cosx的图像用蓝色、实线、三角形标注（要求写出语句，......
2023-11-20
-
坐标系统和计算网格详解详细阅读
5.5.4.3自适应计算网格生成河床及河岸的冲淤与其附近区域的水沙运动有十分密切关系，要求河道演变数学模型对河床及河岸附近流场和含沙场有较高的分辨率，采用固定网格会造成边岸有效网格呈现出阶梯状分布而降低河床和边岸附近的计算精度。......
2023-06-22
-
《高等数学基础》MATLAB：积分求解详细阅读
一、求积分求积分由函数int来实现.该函数的一般调用格式为：int（s）：没有指定积分变量和积分阶数时，系统按默认变量对被积函数或符号表达式s求不定积分.int（s，v）：以v为自变量，对被积函数或符号表达式s求不定积分.int（s，v，a，b）：求定积分运算.a，b分别表示定积分的下限和上限.该函数求被积函数在区间[a，b]上的定积分.a和b可以是两个具体的数，也可以是一个符号表达式，还可以是无......
2023-11-20
-
连续性方程在直角坐标系中的应用详细阅读
欧拉连续性方程是欧拉在1755年建立的。按欧拉方法，如图1.12所示，首先选取控制体元——固定在空间上的一个确定的、形状任意的封闭体积，位置保持不变。控制体元可以非常小，如小到前文所述的特征体元；或者有限大，这需要根据研究问题所确定。控制体元的形状不会影响所得到的方程。ρv也称质量速度，它是单位时间内通过单位面积的流体质量。......
2023-06-28
-
平面直角坐标系教学第一课-简易指南详细阅读
达成目标的标志：体会用有序数对表示物体的位置是将数与形建立了联系。教师给出有序数对的概念：上面的活动是通过像“第2列第4排、第5列第6排”这样含有两个数的表达方式来表示一个确定的位置，其中两个数各自表示不同的含义。......
2023-08-05
相关推荐