知识要点一、函数的概念1.函数、反函数、基本初等函数、初等函数、复合函数的定义.2.理解函数记号y=f（x）中“f”的意义.函数的两个要素，对于两个或两个以上的函数，只有定义域和对应法则完全相同时才是同一函数.3.弄清基本初等函数的概念，熟悉这些函数的特性.4.求f（x）的定义域.对于较复杂的函数求定义域问题，就是求解由简单函数的定义域所构成的不等式组的解集.5.函数的重要性质：有界性，奇偶性，周......
2023-10-26
二元函数极限与连续-高等数学基础
【摘要】：一、二元函数【知识点回顾】函数的定义：设有两个非空集合M、N，如果当变量x在M内任意取定一个数值时，按照确定的法则f，在N内有唯一的y与它相对应，则称y是x的函数.通常x称为自变量，变量x的取值范围M称为这个函数的定义域；y称为函数（或因变量），变量y的取值范围称为这个函数的值域.【例题1】长方形的面积S与长x（x＞0）与宽y（y＞0）的关系S=xy，当x与y变化时，都有唯一的S值和它对应.【例
一、二元函数
【知识点回顾】
函数的定义：设有两个非空集合M、N，如果当变量x在M内任意取定一个数值时，按照确定的法则f，在N内有唯一的y与它相对应，则称y是x的函数.通常x称为自变量，变量x的取值范围M称为这个函数的定义域；y称为函数（或因变量），变量y的取值范围称为这个函数的值域.
【例题1】 长方形的面积S与长x（x＞0）与宽y（y＞0）的关系S=xy，当x与y变化时，都有唯一的S值和它对应.
【例题2】 圆柱体的面体积V与底面半径r（r＞0）与高h（h＞0）的关系V=πr2h，当r与h变化时，都有唯一的V值与其对应.
由例题1，例题2可得出二元函数的定义.
1.二元函数的定义
定义1 设有给定的区域D，M，当变量x与y在区域D中变化时，按照某种对应法则，在区域M中都有唯一的z和它对应，那么变量z称为变量x与y的二元函数.
记作：z=f（x，y）.其中x与y称为自变量，z称为x与y的函数，f称为对应法则，区域D称为函数的定义域，区域M称为函数的值域.
类似的可以定义三元函数w=f（x，y，z），四元函数等，我们把二元及二元以上的函数称为多元函数.这一章对多元函数的讨论主要以二元函数为主.
2.二元函数值记号
【例题3】 设f（x，y）=x2-2xy+y2，求f（1，2）和f（a，b）.
解：f（1，2）=12-2×1×2+22=1；
f(a,b)=a2-2×a×b+b2=(a-b)2.
3.二元函数定义域
【知识点回顾】
y=f（x）函数的定义域是指使得x有意义的一切实数组成的集合.对定义域的求法有如下几种类型：
（1）分式中分母不为零；
（2）偶次根式中内容不能为负；
（3）对数函数中，真数必大于零，底数大于零且不等于1；
（4）在反正弦函数、反余弦函数中，x满足|x|≤1.
y=f（x，y）即变量x与y的变化范围.我们知道一元函数的定义域一般来说是数轴上一个或几个区间.二元函数的定义域通常是由平面坐标系上一条或几段光滑曲线所围成的区域.
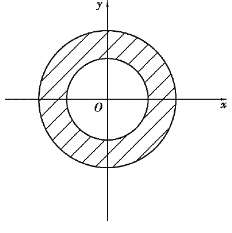
解：函数的定义域满足x2+y2≤1，它在平面坐标系中表示单位闭圆域.
【例题5】 求函数z=ln（x+y）的定义域.
解：函数的定义域满足x+y＞0.它的定义域是位于直线y=-x上方而不包括这条直线在内的半平面（图8.1），这是一个无界开区域.
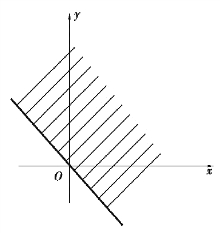
图8.1
(www.chuimin.cn)
图8.2
【例题6】 求函数z=arcsin（x2+y2-1）的定义域.
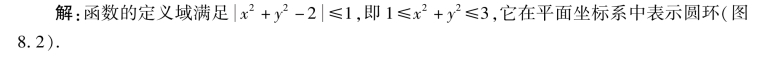
二、二元函数的极限及其连续性
1.二函数的极限
【知识点回顾】
y=f（x）在x=x0处极限的定义：设函数f（x）在x0的某一去心邻域U°（x0，δ）内有定义，当x无限趋近于x0时，相应的函数值f（x）无限趋近于常数A，则称f（x）当x➝x0时以A为极限.
记作
定义2 设二元函数z=f（x，y）在点（x0，y0）的某去心邻域内有定义，点（x，y）为去心邻域内异于（x0，y0）的任意一点，如果当点（x，y）以任意方式趋向于点（x0，y0）时，对应的函数值f（x，y）总趋向于一个确定的常数A，则称A是二元函数z=f（x，y）当（x，y）➝（x0，y0）时的极限，记为
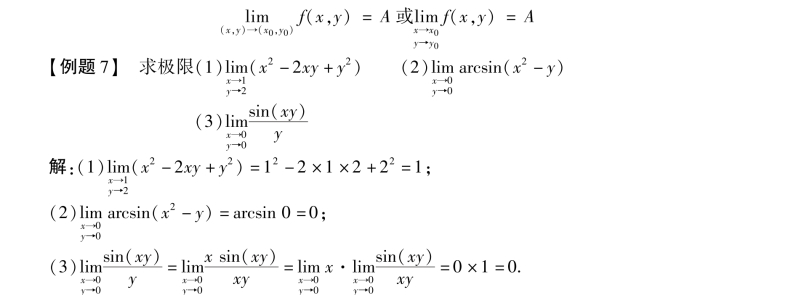
2.二元函数的连续性
【知识点回顾】
y=f（x）连续的定义：设函数y=f（x），当自变量x在x0点有一个增量（改变量）Δx时，相应的函数y的增量Δy=f（x0+Δx）-f（x0），当Δx趋近0时，Δy也趋近于0，则称函数f（x）在点x0处连续.
定义3 如果二元函数z=f（x，y）在点（x0，x0）的一个邻域内有定义，则在点（x0，y0）的增
量分别为Δx=x0+Δx0，Δy=y0+Δy0则有
如满足：
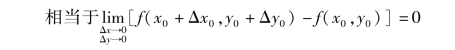
那么称函数z=f（x，y）在点（x0，y0）处连续.
如果f（x，y）在区域D的每一点都连续，那么称它在区域D连续.3.有界闭区域上连续函数的性质
性质1（最大值和最小值定理） 在有界闭区间D上连续的二元函数，在D上一定有最大值和最小值.
性质2（介值定理） 在有界闭区间D上连续的二元函数，必取得介于最大值和最小值的任何值.
习题8.1
6.求下列函数的极限.
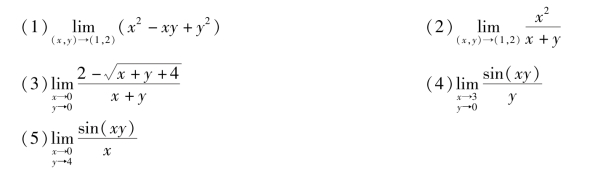
有关高等数学基础的文章
- 详细阅读
-
高等数学第2版：二元函数连续性详细阅读
定义3 设二元函数f（x，y）在开区域（或闭区域）D内有定义，P0（x0，y0）是D内的点（或边界点且P0∈D），如果则称函数f（x，y）在点P0（x0，y0）连续.如果函数f（x，y）在开区域（或闭区域）D内的每一点连续，那么就称函数f（x，y）在D内连续，或者称f（x，y）是D内的连续函数.若函数f（x，y）在点P0（x0，y0）处不连续，则称P0为函数f（x，y）的间断点.前面已经讨论过的函......
2023-10-19
-
复变函数的极限与连续性详解详细阅读
复变函数和实变函数类似,同样可以讨论函数的极限和连续性,且形式基本上与实变函数一致.现在介绍复变函数的极限概念.定义3 设函数w = f(z)在点z0的去心邻域:0 ＜|z - z0| ＜ρ内有定义.如果存在一个复常数A,使得对于任意给定的ε ＞0,总存在一个实数δ ＞0(δ ＜ρ),当0 ＜|z-z0|＜δ 时,有|f(z)-A|＜ε,我们称A为f(z)当z趋于z0时的极限,记为复变函数极限的几......
2023-10-30
-
一、二元函数极限与连续、偏导数及二阶偏导数计详细阅读
【主要内容】1.二元函数极限与连续的概念设二元函数f（x，y）在点（x0，y0）的某个去心邻域{（x，y）|0<（x-x0）2+（y-y0）2<δ2}（其中，δ是某正数）内有定义.如果动点（x，y）以任何方式无限趋于点（x0，y0）时，f（x，y）总是无限趋于常数A，则称A是点（x，y）趋于点（x0，y0）（记为（x，y）→（x0，y0））时f（x，y）的极限，记为或注 根据定义，可以按以下方法判......
2023-10-27
-
高等数学基础：连续函数概念及示例详细阅读
一、连续函数的概念在自然界中有许多现象都是连续不断地变化的，如，气温随着时间的变化而连续变化；金属轴的长度随气温有极微小的改变也是连续变化的等.这些现象反映在数量关系上就是我们所说的连续性.函数的连续性反映在几何上可以看作一条不间断的曲线；下面给出连续函数的概念.（一）函数的增量增量的定义，简单说，就是变化后的量减去变化前的量.例如：早晨t1=8时，温度T1=2℃，中午t2=14时，温度T2=12......
2023-11-20
- 详细阅读
-
高等数学基础：函数性质概述详细阅读
一、函数的有界性如果对属于某一区间I的所有x值总有│f（x）│≤M成立，其中M是一个与x无关的常数，那么我们就称f（x）在区间I有界，否则便称无界.注：一个函数，如果在其整个定义域内有界，则称为有界函数.例如：函数y=cosx在（-∞，+∞）内是有界的.再如：当x∈（-∞，+∞）时，恒有|sinx|≤1，所以函数f（x）=sinx在（-∞，+∞）内是有界函数.这里M=1（当然，也可以取大于1的任何......
2023-11-20
-
函数极限与左、右极限关系详细阅读
【主要内容】1.设函数f（x）在点x0的某个去心邻域内有定义，则limx的充分必要条件是注 （ⅰ）对任意ε>0，如果存在δ>0，当0<|x-x0|<δ时有|f（x）-A|<ε.对任意ε>0，存在δ>0，使得-δ
2023-10-27
相关推荐