高等数学基础：曲面和曲线介绍

2023-11-20 理论教育版权反馈

【摘要】：在上节，我们已经介绍了曲面及曲面方程的概念.如果曲面Σ上每一点的坐标都满足方程F（x，y，z）=0，而不在曲面Σ上的每一点坐标都不满足方程F（x，y，z）=0，则称方程F（x，y，z）=0为曲面方程，称曲面Σ为F（x，y，z）=0的图形.在空间直角坐标系中，如果F（x，y，z）=0是二次方程，则它的图形称为二次曲面.下面给出几种常见的曲面方程，如下所述.一、球面方程空间一动点到定点的距离为定值，该

在上节，我们已经介绍了曲面及曲面方程的概念.如果曲面Σ上每一点的坐标都满足方程F（x，y，z）=0，而不在曲面Σ上的每一点坐标都不满足方程F（x，y，z）=0，则称方程F（x，y，z）=0为曲面方程，称曲面Σ为F（x，y，z）=0的图形.

在空间直角坐标系中，如果F（x，y，z）=0是二次方程，则它的图形称为二次曲面.下面给出几种常见的曲面方程，如下所述.

一、球面方程

空间一动点到定点的距离为定值，该动点的轨迹称为球面，定点称为球心，定值称为半径.设动点M（x，y，z），以P0（x0，y0，z0）为球心，R为球半径，由两点间的距离公式，得

pagenumber_ebook=154,pagenumber_book=146

二、柱面方程

直线L沿定曲线C平行移动所形成的曲面称为柱面.定曲线C称为柱面的准线，动直线L称为柱面的母线.如果柱面的准线C在xOy坐标面上的方程为f（x，y）=0，那么以C为准线，母线平行于z轴的柱面方程就是f（x，y）=0；同样地，方程g（y，z）=0表示母线平行于x轴的柱面方程；方程h（x，z）=0表示母线平行于y轴的柱面方程.一般地，在空间直角坐标系中，含有两个变量的方程就是柱面方程，且在其方程中缺哪个变量，此柱面的母线就平行于哪一个坐标轴.

例如，一个圆柱面的母线平行于z轴，准线C是在xOy坐标面上的以原点为圆心，R为半径的圆，即准线C在xOy坐标面上的方程为x2+y2=R2，其圆柱面方程为

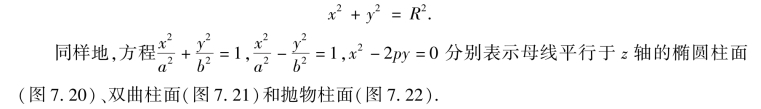
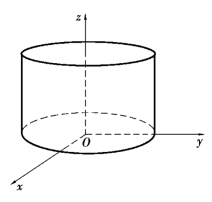
pagenumber_ebook=154,pagenumber_book=146

图7.20

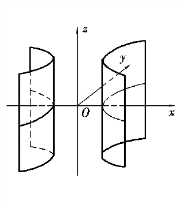
pagenumber_ebook=154,pagenumber_book=146

图7.21

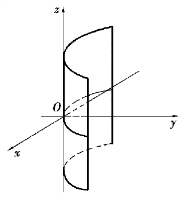
pagenumber_ebook=154,pagenumber_book=146

图7.22

三、以坐标轴为旋转轴的旋转曲面

一条曲线C绕一定直线L旋转所生成的曲面称为旋转曲面.曲线C称为旋转曲面的母线，定直线L称为旋转曲面的旋转轴（或者称为轴）.

以下只讨论母线在某个坐标平面上的平面曲线，而旋转轴是该坐标平面上的一条坐标轴的旋转曲面.

设在yOz平面上有一条曲线C，它在平面直角坐标系中的方程为f（y，z）=0，现在来求曲线C绕z轴旋转所生成的旋转曲面方程.

pagenumber_ebook=155,pagenumber_book=147

图7.23

对于其他坐标面上的曲线，绕它所在坐标面的一条坐标轴旋转所得的旋转曲面的方程可以类似求出，这样可得出如下规律.

当坐标平面上的曲线C绕此坐标平面里的一条坐标轴旋转时，为了求出这样的旋转曲面的方程，只要将曲线C在坐标面里的方程保留和旋转轴同名的坐标，而用其他两个坐标平方和的平方根来代替方程中的另一坐标即可.

四、几种特殊的二次曲面

1.椭球面方程为

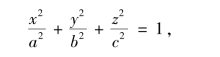
pagenumber_ebook=155,pagenumber_book=147

其形状如图7.24所示.

2.抛物面

例：椭圆抛物面方程为

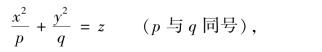
pagenumber_ebook=155,pagenumber_book=147

其形状如图7.25所示.

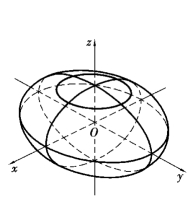
pagenumber_ebook=155,pagenumber_book=147

图7.24

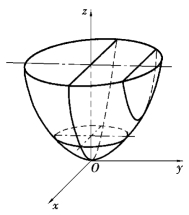
pagenumber_ebook=155,pagenumber_book=147

图7.25　

旋转抛物面方程为

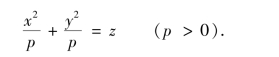
pagenumber_ebook=156,pagenumber_book=148

双曲抛物面（鞍形曲面）方程为

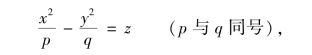
pagenumber_ebook=156,pagenumber_book=148

当p＞0，q＞0时，其形状如图7.26所示.

3.双曲面

单叶双曲面方程为

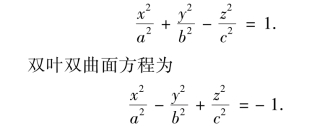
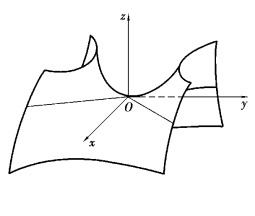
pagenumber_ebook=156,pagenumber_book=148

图7.26

注意各种图形规律特点，可以写出其他的方程表达式.

习题7.6

1.方程x2+y2+z2-2x+4y+2z=0表示什么曲面？

2.已知球面的一条直径的两个端点是（2，-3，5）和（4，1，-3），写出球面的方程.

3.指出下列方程表示什么曲面，并作出它们的草图.

(1)y=2x2(2)x2-y2=1

(3)x2+y2=0(4)x-y=0

4.说明下列旋转曲面是怎样形成的.(www.chuimin.cn)

(1)x2+2y2+3z2=1(2)x2+y2=z2

5.把zOx面上的抛物线z=x2+1绕z轴旋转一周，求所形成的旋转曲面方程.

6.求xOy面上的直线x+y=1绕y轴旋转一周所形成的旋转曲面方程.

7.分别写出曲面x2+y2+z2=25在下列各平面上的截痕的方程，并指出是什么曲线.

(1)x=2　(2)y=5　(3)z=1

复习题七

一、填空题

1.在空间直角坐标系中，写出点P（1，2，3）的对称点的坐标.

（1）关于x轴的对称点是__________________；

（2）关于y轴的对称点是__________________；

（3）关于z轴的对称点是_________________；

（4）关于原点的对称点是_________________；

（5）关于xOy坐标平面的对称点是_________________；

（6）关于yOz坐标平面的对称点是_________________；

（7）关于xOz坐标平面的对称点是_________________.

2.在空间直角坐标系中，写出点P（1，2，3）的投影点的坐标：

（1）关于x轴的投影点是_________________；

（2）关于y轴的投影点是__________________；

（3）关于z轴的投影点是_________________；

（4）关于原点的投影点是__________________；

（5）关于xOy坐标平面的投影点是_________________；

（6）关于yOz坐标平面的投影点是_________________；

（7）关于xOz坐标平面的投影点是_________________.

3.向量（5，1，-3）的模是__________________.

4.已知a={1，2，-1}，b={2，0，k}，且满足a⊥b，则k=____________________.

5.点M（-2，5，3）到平面4x-3y+z+7=0的距离是_________________.

二、选择题

1.在空间直角坐标系中，

（1）在Ox轴上的点的坐标可表示为（0，b，0）；

（2）在yOz平面上点的坐标可以写成（0，b，c）；

（3）在Oz轴上的点的坐标可记为（0，0，c）；

（4）在xOz平面上点的坐标可写为（a，0，c）.

其中正确的叙述的个数是（　）.

A.1　B.2　C.3　D.4

2.向量a={0，0，1}的同方向的单位向量a0为（　）.

3.平面x+2y+3z-6=0在x轴上的截距为（　）.

A.6　B.3　C.2　D.1

4.已知a={2，4，k}，b={1，2，-2}，满足a平行于b，则k=（　）.

A.-2　B.2　C.-4　D.4

5.已知A（0，1，1），B（1，3，3），则|AB|=（　）.

A.4　B.3　C.2　D.1

三、计算应用题

1.设A，B两点为A（2，y，1），B（-2，2，2），它们之间的距离为|AB|=7，求点A的未知坐标y.

pagenumber_ebook=158,pagenumber_book=150

6.已知a={1，2，0}，b={1，0，2}，求a·b，cos＜a，b＞.

7.已知a={1，1，1}，b={2，2，2}，求以a，b为边的平行四边形的面积.

8.求平行于x轴，且经过点（4，0，-2）和（5，1，7）的平面方程.

9.一平面过点M（1，1，-1），且在x轴和z轴上的截距分别为2和1，求此平面方程.

10.求经过两点M1（1，0，2），M2（2，1，4）的直线方程.

11.一直线经过点（2，-3，4），且垂直于平面3x-y+2z=4，求此直线方程.

pagenumber_ebook=158,pagenumber_book=150

哥德巴赫猜想第一人——陈景润

高等数学基础：曲面和曲线介绍

相关推荐