一、点的轨迹方程的概念在平面解析几何中，把平面曲线看作一个动点运动的轨迹，从而得到轨迹方程——曲线方程的概念.则在空间解析几何中，也可以将曲面或曲线看作是满足一定条件的动点的轨迹，动点的轨迹也用方程或方程组来表示，从而得到曲面方程或曲线方程的概念.如果曲面Σ与三元方程f（x，y，z）=0有如下关系：曲面Σ任意一点的坐标都满足方程f（x，y，z）=0；不在曲面Σ上的点的坐标都不满足方程f（x，y，z......
2023-11-20
高等数学基础-直线方程及其应用
【摘要】：一、直线的一般式方程空间中任何一条直线都可以看作两个相交平面的交线.如果直线L作为平面A1x+B1y+C1z+D1=0和平面A2x+B2y+C2z+D2=0的交线，则该直线L的一般式方程为其中{A1，B1，C1}与{A2，B2，C2}不成比例.二、直线的标准式方程由立体几何可知，过空间一点作平行于已知直线的直线是唯一的.因此，如果知道直线上一点及直线平行与某一向量，那么，该直线的位置就唯一确定.下
一、直线的一般式方程
空间中任何一条直线都可以看作两个相交平面的交线.如果直线L作为平面A1x+B1y+C1z+D1=0和平面A2x+B2y+C2z+D2=0的交线，则该直线L的一般式方程为
其中{A1，B1，C1}与{A2，B2，C2}不成比例.
二、直线的标准式方程
由立体几何可知，过空间一点作平行于已知直线的直线是唯一的.因此，如果知道直线上一点及直线平行与某一向量，那么，该直线的位置就唯一确定.下面，我们利用此结论推导直线的方程.
方向向量的定义：如果一个非零向量s平行于直线L，则称s为直线L的方向向量.任意方向向量的坐标称为直线的一组方向数.显然，一条直线的方向向量有无穷多个，它们之间互相平行.
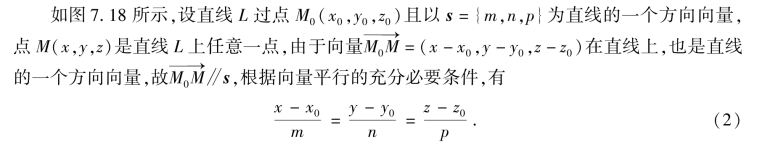
图7.18
此即直线L的标准式方程（也称为点向式方程或对称式方程）.
注：在（2）式中，若有个别分母为零，应相应地理解为其所对应的分子也为零.
【例题1】 求过点P（1，2，3）且方向向量s={1，2，2}的直线方程.
解：由直线的点向式方程可得
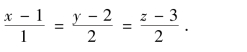
【例题2】 求过点M1（1，2，2）、M2（0，1，-1）的直线方程.
即
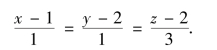
【例题3】 求过点P（1，2，3）且与平面L：2x+3y-z+1=0垂直的直线方程.
解：由s=nL={2，3，-1}，由直线的点向式方程可得
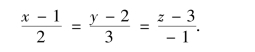
三、直线的参数方程
由直线的标准方程引入变量t，令
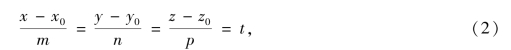
则有
此即过点M0（x0，y0，z0）且以s={m，n，p}为方向向量的直线L的参数方程，其中t为参数.
其中t为参数.
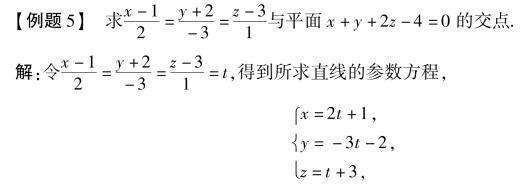(www.chuimin.cn)
其中t为参数.
将此参数方程代入平面方程x+y+2z-4=0得：
即t=-1，即x=-1，y=1，z=2，所以交点为（-1，1，2）.
四、两条直线的位置关系
由立体几何知识可知，空间中直线的位置关系有相交、平行、异面3种情况，下面我们分别考虑空间中两条直线的位置关系.
【例题6】 已知直线L1、L2，判断它们之间的位置关系：
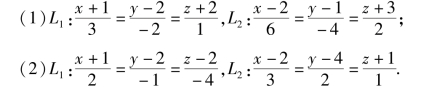
解：（1）因为直线L1和L2的方向向量分别为s1=（3，-2，1）、
s2=（6，-4，2），s1∥s2，所以，L1∥L2；
（2）因为直线L1和L2的方向向量分别为s1=（2，-1，-4）、s2=（3，2，1），s1⊥s2，所以L1⊥L2.
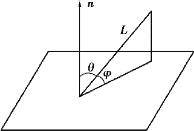
图7.19
设直线L和平面π的方程分别为
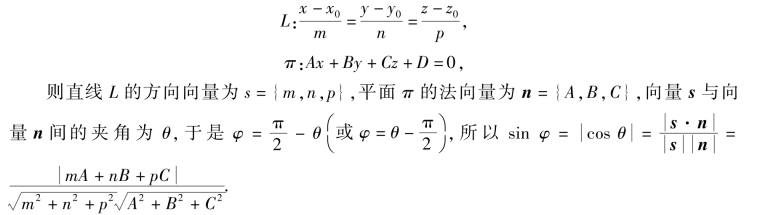
由直线与平面的位置关系：
（1）平行：L∥π⇔s⊥n（或mA+nB+pC=0）且M0（x0，y0，z0）在L上，而不在π内；
（2）重合：L在π内⇔s⊥n（或mA+nB+pC=0）且M0（x0，y0，z0）既在L上，又在π内；
习题7.5
1.求过点P（1，2，3）且方向向量s={3，2，1}的直线方程.
2.求经过两点M1（1，0，-1），M2（2，1，-2）的直线方程.
4.求过点（3，4，-4）且与平面9x-4y+2z-1=0垂直的直线方程.
7.已知直线L1、L2，判断它们之间的位置关系：
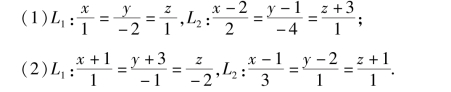
8.已知直线L和平面π，判断它们之间的关系.
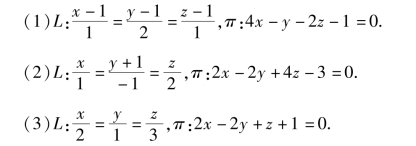
有关高等数学基础的文章
- 详细阅读
-
直线方程与倾斜角：机电应用数学导读详细阅读
1.直线的倾斜角与斜率（1）倾斜角观察图4-10，直线l在直角坐标系中与两条坐标轴有不同的夹角，规定：直线l向上的方向与x轴的正方向所成的最小正角，叫做直线l的倾斜角.如图4-10中的α.注意：1）从运动变化的观点来看，直线的倾斜角是由x轴绕交点按逆时针方向转到与直线重合时所成的角；2）规定：直线与x轴平行或重合时，直线的倾斜角为0°；3）直线倾斜角α的取值范围是：0°≤α<180°；4）在同一直......
2023-11-22
-
高等数学：变力沿直线做功详细阅读
解如图6－25所示建立坐标系.取x为积分变量，x∈［2，8］.图6－25考察区间［x，x＋dx］上的一薄层水，将这薄层水“提到”池口的距离为x，将这层水抽出，克服重力所做的功为于是......
2023-11-19
-
复平面曲线方程及其应用详细阅读
实平面上曲线有直角坐标方程和参数方程两种形式，复平面上的曲线也有直角坐标方程和参数方程两种复数形式.(1)直角坐标方程设z =x+iy,若平面曲线C的直角坐标方程为F(x,y)=0,由可得平面曲线C在复平面上复数形式的方程例1 把直线方程3x+2y =1化为复数形式.解 将代入方程,得为所给直线方程的复数形式.(2)参数方程令z =x+iy,若平面曲线C的参数方程为x=x(t),y =y(t)(α......
2023-10-30
-
解一阶线性微分方程-高等数学基础详细阅读
形如y′+p（x）y=q（x），其中，p，q与y，y′无关，但可以与x有关.它对y与y′而言是一次的，故称之为一阶线性微分方程.当q（x）=0时称为齐次线性微分方程；当q（x）≠0时称为非齐次线性微分方程.一、齐次线性微分方程的解法齐次线性微分方程的形式为：y′+p（x）y=0.此方程是可分离变量的微分方程，分离变量后，得：两边积分得：ln|y|=-∫p（x）dx，这就是齐次线性微分方程的一般解.......
2023-11-20
-
直线与曲线设计基础：垂直线、水平线、斜线、折详细阅读
直线分为垂直线、水平线、斜线、折线，还可分为粗线、细线等。斜线极容易与短跑运动员起跑、飞机脱离地面腾空而起或溜冰的姿态联系起来，表达重心前移，表现出一种前冲的力量，具有不稳定感。几何曲线，是按一定规则绘制而成的曲线，有温暖的性格。几何曲线的典型表现是圆周线，它有对称美和秩序美。......
2023-10-12
-
高等数学基础：定积分在几何上的应用详细阅读
一、定积分的元素法（微元法）在定积分的应用中，人们经常采用所谓的元素法，为此，回顾一下之前讨论过的曲边梯形的面积计算方法.设f在区间[a，b]上连续，且f≥0，求以曲线y=f为曲边，底为[a，b]的曲边梯形的面积A，如图5.9所示.图5.9（一）分割用任意一组分点a=x0＜x1＜…......
2023-11-20
-
逻辑斯蒂方程简介-高等数学详细阅读
逻辑斯蒂方程是一种在许多领域中都有着广泛应用的数学模型，下面我们通过树的生长过程的例子来说明该模型的建立过程.一棵小树刚栽下去的时候长得比较慢，渐渐地，小树长高了，而且长得越来越快，但长到某一高度后，它的生长速度趋于稳定，然后再慢慢降下来.这一现象具有普遍性.现在我们来建立这种现象的数学模型.如果假设树的生长速度与它目前的高度成正比，则显然不符合两头尤其是后期的生长情形，因为树不可能越长越快；但如......
2023-10-19
相关推荐