高等数学基础：平面和曲面方程原理

2023-11-20 理论教育版权反馈

【摘要】：一、点的轨迹方程的概念在平面解析几何中，把平面曲线看作一个动点运动的轨迹，从而得到轨迹方程——曲线方程的概念.则在空间解析几何中，也可以将曲面或曲线看作是满足一定条件的动点的轨迹，动点的轨迹也用方程或方程组来表示，从而得到曲面方程或曲线方程的概念.如果曲面Σ与三元方程f（x，y，z）=0有如下关系：曲面Σ任意一点的坐标都满足方程f（x，y，z）=0；不在曲面Σ上的点的坐标都不满足方程f（x，y，z

一、点的轨迹方程的概念

在平面解析几何中，把平面曲线看作一个动点运动的轨迹，从而得到轨迹方程——曲线方程的概念.则在空间解析几何中，也可以将曲面或曲线看作是满足一定条件的动点的轨迹，动点的轨迹也用方程或方程组来表示，从而得到曲面方程或曲线方程的概念.

如果曲面Σ与三元方程f（x，y，z）=0有如下关系：

曲面Σ任意一点的坐标都满足方程f（x，y，z）=0；

不在曲面Σ上的点的坐标都不满足方程f（x，y，z）=0，

则称方程f（x，y，z）=0是曲面Σ的方程，曲面Σ就称为方程f（x，y，z）=0的图形.

于是，空间曲线可以看作两个曲面的交线.

二、平面及其方程

1.平面的点法式方程

法向量的定义：如果一非零向量n垂直于平面π，则称此向量为该平面的法向量.显然，平面的法向量有无数个，它们均垂直于平面π内的任意向量.

由立体几何的知识可知，已知平面上的一点M0（x0，y0，z0）和其法向量n={A，B，C}就可以唯一确定这个平面，如图7.15所示，设平面π过点M0（x0，y0，z0），以n={A，B，C}为法向量，现求平面π的点法式方程.

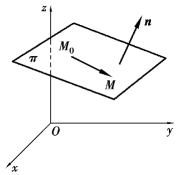
pagenumber_ebook=145,pagenumber_book=137

图7.15

（1）式为平面的点法式方程.

【例题1】　求过点（1，2，3），法向量n={2，3，1}的平面方程.解：由平面的点法式方程得

即：2x+3y-z-4=0.

2.平面的一般式方程

将A（x-x0）+B（y-y0）+C（z-z0）=0　（A，B，C至少有一个不为零）展开，得Ax+By+Cz-Ax0-By0-Cz0=0.设D=-Ax0-By0-Cz0，于是有

（2）式为平面的一般式方程，这里n={A，B，C}.

【例题2】　求过点（-3，2，1）且与平面L1：2x+3y-z=0平行的平面L方程.

解：由题意知，L//L1，所以n=n1={2，3，-1}，有平面的点法式方程，将点（-3，2，1）代入得

即　2x+3y-z+1=0.

*【例题3】　求经过3点A（1，-1，2），B（3，1，2），C（0，1，3）的平面方程.

pagenumber_ebook=146,pagenumber_book=138

故所求的平面为：2（x-1）-2（y+1）+6（z-2）=0.

即　x-y+3z-8=0.

3.平面的截距式方程

【例题4】　如图7.16所示，设一平面不过原点且与3个坐标轴相交于点M（a，0，0），N（0，b，0），P（0，0，c）3点，求此平面方程.

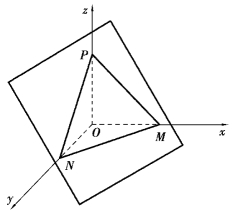
pagenumber_ebook=146,pagenumber_book=138

图7.16

解：由于M，N，P3点在平面上，因此3点的坐标满足平面的方程，设平面的方程为

将M，N，P单点坐标分别带入，则有

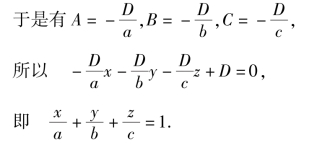
pagenumber_ebook=146,pagenumber_book=138

其中，a，b，c称为平面在空间坐标系上的截距，所以上式被称为平面的截距式方程.

【例题5】　求方程2x+3y+6z=12在x轴，y轴，z轴上的截距.

解：由2x+3y+6z=12得

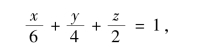
pagenumber_ebook=146,pagenumber_book=138

所以在x轴，y轴，z轴上的截距分别为6，4，2.

4.几种特殊位置平面的方程

（1）通过原点的平面方程

由于平面通过原点，点（0，0，0）满足方程，得D=0，因此，平面方程的一般形式为：　Ax+By+Cz=0.

（2）平行于坐标轴

平行于x轴的平面方程的一般形式为：By+Cz+D=0.

平行于y轴的平面方程的一般形式为：Ax+Cz+D=0.

平行于z轴的平面方程的一般形式为：Ax+By+D=0.

（3）通过坐标轴

通过x轴的平面方程的一般形式为：By+Cz=0.(www.chuimin.cn)

分别通过y轴和z轴的平面方程的一般形式为：Ax+Cz=0，Ax+By=0.

（4）垂直于坐标轴

垂直于x轴、y轴、z轴的平面方程的一般形式为：Ax+D=0，By+D=0，Cz+D=0

特殊地，x=0表示yOz面，y=0表示xOz面，z=0表示xOy面.

特殊地，x=2表示平行于yOz面且与yOz平面的距离为2的平面；y=2表示平行于xOz面且与xOz平面的距离为2的平面；z=2表示平行于xOy面且与xOy平面的距离为2的平面.

【例题6】　求过点（3，-2，3）且平行于xOy坐标面的平面方程.

解：此方程平行于xOy坐标面，即垂直于z轴，设方程为Cz+D=0，将点（3，-2，3）代入方程，得3C+D=0，D=-3C，代回所设方程Cz-3C=0，故所求平面方程为z-3=0.

【例题7】　如图7.17所示，求平行于x轴且过两点（1，2，3）和（2，-1，4）的平面方程.

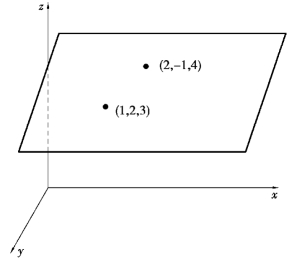
pagenumber_ebook=147,pagenumber_book=139

图7.17

解：因所求平面方程平行于x轴，设方程为By+Cz+D=0，代入两点的坐标，得

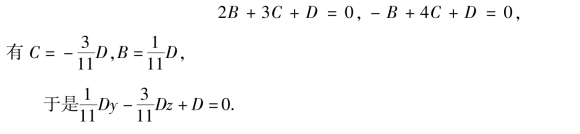
pagenumber_ebook=147,pagenumber_book=139

因D≠0，即得平面方程为y-3z+11=0.

5.两个平面的位置关系

由立体几何的知识，我们知道空间两平面的位置关系有相交、平行和重合3种情形，而且当且仅当两平面有一公共点时相交，当且仅当两平面没有公共点时平行，当且仅当一个平面上的所有点都是另一个平面的点时它们重合.

设两个平面π1与π2的方程分别为

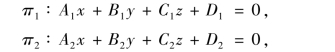
pagenumber_ebook=148,pagenumber_book=140

其法向量分别为n1={A1，B1，C1}，n2={A2，B2，C2}，于是有如下结论：

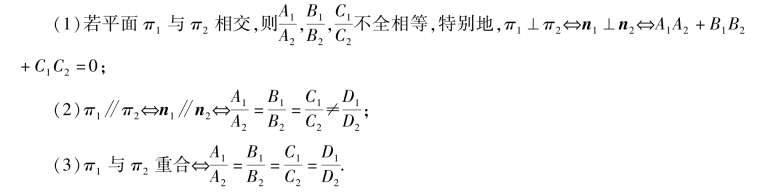
pagenumber_ebook=148,pagenumber_book=140

【例题8】　分别判断下列各组的两个平面的位置关系.

（1）2x-3y+z=0和2x+3y-5z+2=0；

（2）3x+2y-2z+6=0和6x+4y-4z-6=0；

（3）x+y-z-2=0和-2x-2y+2z+4=0；

（4）2x-3y+z=0和2x+3y+5z+2=0.

解：（1）2x-3y+z=0和2x+3y-5z+2=0

pagenumber_ebook=148,pagenumber_book=140

下面，不加证明地给出空间两个平面之间的夹角和点到平面的距离公式.

平面π1与π2的夹角θ，即为两个平面法向量夹角，由两个向量间的夹角公式得：

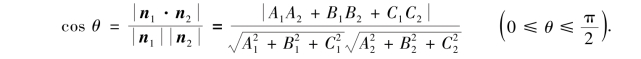
pagenumber_ebook=148,pagenumber_book=140

点P1（x1，y1，z1）到平面π：Ax+By+Cz+D=0的距离公式为

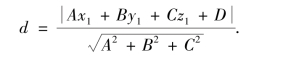
pagenumber_ebook=148,pagenumber_book=140

【例题9】　求平面L1：2x-3y+z=0和L2：2x+3y+5z+2=0的夹角.

解：由n1={2，-3，1}，n2={2，3，5}，

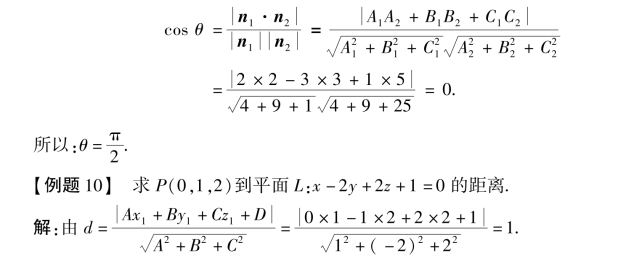
pagenumber_ebook=149,pagenumber_book=141

习题7.4

1.求满足下列条件的平面方程

（1）过点（1，2，3），n={2，3，1}的平面方程.

（2）过点M（1，1，1），且与平面3x-y+2z-1=0平行的平面方程.

（3）与x，y，z轴的交点分别为（2，0，0），（0，3，0）和（0，0，1）的截距式方程.

2.求满足下列条件的平面方程

（1）经过z轴，且过点（-3，1，-2）.

（2）平行于z轴，且经过点（4，0，-2）和（5，1，7）.

（3）平行于zOx面，且过点（2，-5，3）.

3.一平面过点M（2，1，-1），而在x轴和y轴上的截距分别为2和1，求此平面方程.

4.求平面3x+y-2z-6=0在x，y，z坐标轴上的截距，并将平面化为截距式方程.

5.求点M（1，2，1）到平面x+2y+2z-10=0的距离.

6.求两平行平面x+2y+z+2=0和x+2y+z+10=0间的距离.

7.分别判断下列各组的两个平面的位置关系.

（1）x-y+z=0和2x-3y-5z+2=0；

（2）x+2y-2z+6=0和2x+4y-4z-6=0；

（3）x+y-z-2=0和2x-y+2z+4=0；

（4）2x-y+z=0和2x+3y-z+2=0.

高等数学基础：平面和曲面方程原理

相关推荐