首页理论教育向量的坐标表示及线性运算

向量的坐标表示及线性运算

2023-11-20 理论教育版权反馈

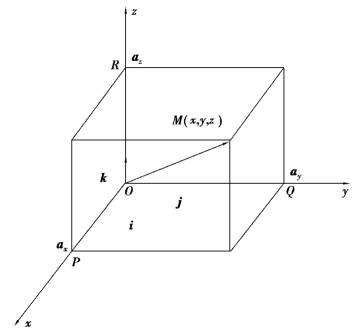
【摘要】：一、向量的坐标表示1.向径的坐标表示图7.13即空间任意向量的坐标等于终点与起点的对应的坐标之差.【例题1】计算二、坐标表示下的向量的线性运算设两个向量a=a1i+a2j+a3k，b=b1i+b2j+b3k，则线性运算有：(1)a+b=(a1+b1)i+(a2+b2)j+(a3+b3)k;(2)a-b=(a1-b1)i+(a2-b2)j+(a3-b3)k;(3)λa=λ(a1i+a2j+a3k)

一、向量的坐标表示

1.向径的坐标表示

pagenumber_ebook=138,pagenumber_book=130

pagenumber_ebook=138,pagenumber_book=130

图7.13

pagenumber_ebook=138,pagenumber_book=130

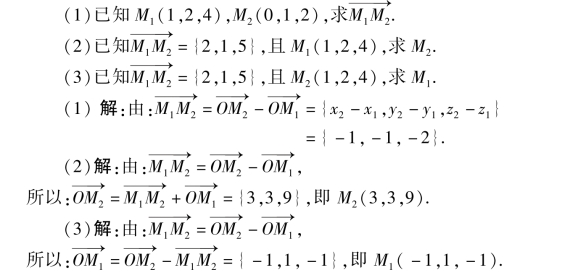
pagenumber_ebook=139,pagenumber_book=131

即空间任意向量的坐标等于终点与起点的对应的坐标之差.

【例题1】　计算

pagenumber_ebook=139,pagenumber_book=131

二、坐标表示下的向量的线性运算

设两个向量a=a1i+a2j+a3k，b=b1i+b2j+b3k，则线性运算有：

(1)a+b=(a1+b1)i+(a2+b2)j+(a3+b3)k;

(2)a-b=(a1-b1)i+(a2-b2)j+(a3-b3)k;

(3)λa=λ(a1i+a2j+a3k)=λa1i+λa2j+λa3k.

【例题2】　已知a={1，3，5}，b={-1，0，4}，求（1）2a；　（2）3a-2　B.

（1）解：2a=2×{1，3，5}={2，6，10}；

（2）解：3a-2b=3×{1，3，5}-2×{-1，0，4}={3，9，15}-{-2，0，8}={5，9，7}.

三、向量的模、方向余弦及坐标表示(www.chuimin.cn)

1.向量的模

已知向量a=（ax，ay，az），则向量a的模为

2.向量的方向余弦

pagenumber_ebook=139,pagenumber_book=131

pagenumber_ebook=140,pagenumber_book=132

图7.14

pagenumber_ebook=140,pagenumber_book=132

所以，3个方向余弦也可用坐标表示为

pagenumber_ebook=140,pagenumber_book=132

由三角函数知识我们可以得到下面的关系式：

与非零向量a同方向的单位向量为：

pagenumber_ebook=140,pagenumber_book=132

pagenumber_ebook=141,pagenumber_book=133

习题7.2

1.计算

pagenumber_ebook=141,pagenumber_book=133