张量积也是一个向量空间，但我们将这个向量空间里的向量称之为张量。张量积还解决了一个特殊的代数问题。它们的张量积VW构成了一个新向量空间，所用的也是同一组标量。参考阅读//No. 7 集合论，第18页No. 8 积，第20页No. 57 向量，第118页No. 76 维度，第156页右图：张量积可以把一个不完全的线性映射转化为一个线性映射。通过取张量积，我们可以将向量空间乘在一起，得到一个新向量空间。......
2023-11-22
空间直角坐标系与向量概念
【摘要】：一、空间直角坐标系在空间，使3条具有相同单位长度的数轴相互垂直且相交于一点O，这3条数轴分别称为x轴、y轴和z轴，一般是把x轴和y轴放置在水平面上，z轴垂直于水平面.z轴的正向按如图7.1所示的右手法则判断，具体规定如下：伸出右手，让四指与大拇指垂直，并使四指先指向x轴的正向，然后让四指沿握拳方向旋转90°指向y轴的正向，这时大拇指所指的方向就是z轴的正向.这样就组成了右手空间直角坐标系Oxyz.
一、空间直角坐标系
在空间，使3条具有相同单位长度的数轴相互垂直且相交于一点O，这3条数轴分别称为x轴、y轴和z轴，一般是把x轴和y轴放置在水平面上，z轴垂直于水平面.z轴的正向按如图7.1所示的右手法则判断，具体规定如下：伸出右手，让四指与大拇指垂直，并使四指先指向x轴的正向，然后让四指沿握拳方向旋转90°指向y轴的正向，这时大拇指所指的方向就是z轴的正向.这样就组成了右手空间直角坐标系Oxyz.
在此空间直角坐标系中，x轴称为横轴，y轴称为纵轴，z轴称为竖轴，O称为坐标原点；每两轴所确定的平面称为坐标平面，简称坐标面.x轴与y轴所确定的坐标面称为xOy坐标面，类似地有yOz坐标面，zOx坐标面.这3个坐标面把空间分为8个部分，每一部分称为一个卦限（图7.2）.x，y，z的正半轴卦限称为第Ⅰ卦限，从Oz轴的正向向下看，按逆时针方向先后出现的卦限依次称为第Ⅱ，Ⅲ，Ⅳ卦限.第Ⅰ，Ⅱ，Ⅲ，Ⅳ卦限下面的空间部分依次称为第Ⅴ，Ⅵ，Ⅶ，Ⅷ卦限.
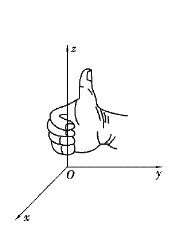
图7.1
图7.2
设点M为空间的一个定点，过点M分别作垂直于x，y，z轴的平面，依次交x，y，z轴于点P，Q，R，设点P，Q，R在x，y，z轴上的坐标分别为x，y，z，那么就得到与点M对应唯一确定的有序实数组（x，y，z）；反之，已知有序实数组（x，y，z），依次在x，y，z轴上找出坐标是x，y，z的3点P，Q，R，分别过这3点作垂直于3个坐标轴的平面，必然相交于空间一点M，则有序实数组有唯一对应空间一点M，由此，空间任意一点与有序实数组（x，y，z）之间存在着一一对应关系.（x，y，z）称为点M的坐标，记作M（x，y，z），这样就确定了M点的空间坐标，其中x，y，z分别称为点M的横坐标、纵坐标、竖坐标（图7.3）.
由上述规定可知，图7.3中的顶点O，P，Q，R的坐标分别为O（0，0，0），P（x，0，0），Q（0，y，0），R（0，0，z）.
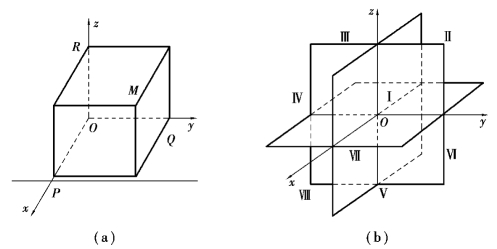
图7.3
1.投影点
M点在x轴上投影点为P（x，0，0），M点在y轴上投影点为Q（0，y，0），M点在z轴上投影点为R（0，0，z）.
M点在xOy面上投影点为P0（x，y，0），M点在yOz面上投影点为Q0（0，y，z），M点在xOz面上投影点为R0（x，0，z）.
2.对称点
M点在x轴上对称点为P′（x，-y，-z），M点在y轴上对称点为Q′（-x，y，-z），M点在z轴上对称点为R′（-x，-y，z）.
M点在xOy面上对称点为P″（x，y，-z），M点在yOz面上对称点为Q″（-x，y，z），M点在xOz面上对称点为R″（x，-y，z）.
M点关于原点的对称点为M0（-x，-y，-z）.
【例题1】 已知空间中的一点M（3，2，4）.
（1）分别写出点M在xOy，yOz，zOx平面上的投影点.
（2）分别写出点M在x，y，z轴上的投影点.
（3）写出点M关于原点对称的点.
解：由空间直角坐标系点的知识可知：
（1）点M在xOy，yOz，zOx平面上的投影点分别是M1（3，2，0），M2（0，2，4），M3（3，0，4）.
（2）点M在x，y，z轴上的投影点分别是N1（3，0，0），N2（0，2，0），N3（0，0，4）.
（3）点M关于原点对称的点为L（-3，-2，-4）.
二、空间两点间的距离公式
图7.4
【例题3】 求空间一点M（3，5，-2）到坐标轴及到坐标面的距离.
解：为了利用两点间的距离公式，我们将点到坐标轴的距离转化为空间两点间的距离来进行计算.设点M在X，Y，Z3个坐标轴上的投影分别是A，B，C，其坐标分别是A（3，0，0），B（0，5，0），C（0，0，-2），则由两点间的距离公式得
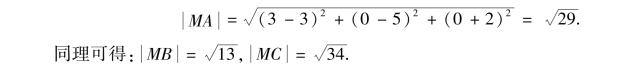
将点到平面的距离转化为点到平面的投影点间的距离.设点M在xOy，yOz，zOx3个坐标面上的投影分别是D、E、F，其坐标分别是D（3，5，0）、E（0，5，-2）、F（3，0，-2），则由两点间的距离公式得
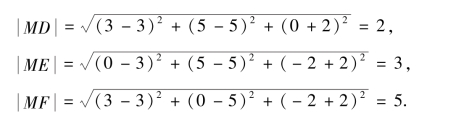
三、向量的基本概念
向量：我们通常遇到的量有两类，一类是只有大小没有方向的量，如长度、面积、体积、温度等，这一类量称为数量.另一类量既有大小又有方向，如力、速度、位移等，这一类量称为向量或矢量.可以在空间自由平行移动的向量，称为自由向量.本教材若不特别说明，向量均指自由向量.
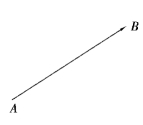
图7.5
图7.6
负向量：与向量a的模相等而方向相反的向量称为a的负向量，记作-a.
向量的相等：两个向量a与b不论起点是否一致，只要大小相等，方向相反，就称a与b相等，记作a= B.
向量的夹角：将空间中的两个非零向量的起点平移在一起时，两个向量正向之间的夹角定义为向量a与b的夹角，记作＜a，b＞.显然有＜a，b＞∈[0，π]，如图7.6所示.
这样，当＜a，b＞=0或π时，两个向量方向相同或相反，称向量a与b平行，记作a∥ B.当＜a，b＞=π/2时，称向量a与b垂直，记作a⊥ B.由于零向量的方向为任意方向，因此，零向量与任意向量平行或垂直.
向量的投影：
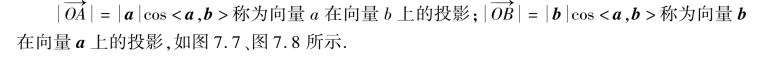(www.chuimin.cn)
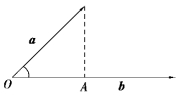
图7.7
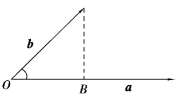
图7.8
四、向量的线性运算
1.向量的和
①三角形法则.若将向量a的终点与向量b的起点放在一起，则以a的起点为起点，以b的终点为终点的向量称为向量a与b的和向量，记为a+ B.这种求向量和的方法称为向量加法的三角形法则，如图7.9所示.
②平行四边形法则.将两个向量a和b的起点放在一起，并以a和b为邻边作平行四边形，则从起点到对角顶点的向量称为a+ B.这种求向量和的方法称为向量加法的平行四边形法则，如图7.10所示.
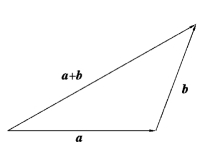
图7.9
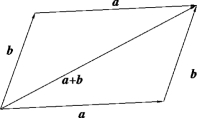
图7.10
显然，向量的加法满足下列运算律.
交换律：a+b=b+a；
结合律：（a+b）+c=a+（b+c）.
2.向量的减法
两向量的减法（即向量的差）规定为a-b=a+（-1） B.
向量的减法三角形法则：只要把a与b的起点放在一起，a-b即是以b的终点为起点，以a的终点为终点的向量，如图7.11（a）（b）所示.
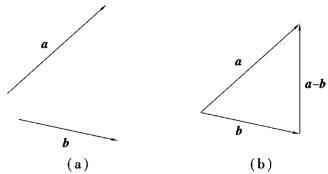
图7.11
3.数与向量的乘法运算
实数λ与向量a的乘积是一个向量，称为向量a与数λ的乘积，记作λa，并且规定：
②方向：当λ＞0时，λa与a的方向相同；当λ＜0时，λa与a的方向相反；λ=0时，λa是零向量.
设λ，μ都是实数，则数与向量的乘法满足下列运算律：
结合律：λ（μa）=（λμ）a=μ（λa）；
分配律：（λ+μ）a=λa+μa，λ（a+b）=λa+λ B.
4.单位向量：模为1的向量称为单位向量.
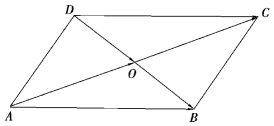
图7.12
根据三角形法则，有
习题7.1
1.在空间直角坐标系中说明下列各点的位置.
A(-3,1,2), B(1,3,-2), C(1,-3,-2),
D(-3,0,-4),E(0,2,2),F(-2,4,-2).
2.求点M（1，-2，4）关于各坐标面、各坐标轴的投影点的坐标.
3.求点M（1，2，3）关于下列条件的对称点的坐标.
（1）各坐标面（2）各坐标轴（3）坐标原点
4.求下列两点间的距离
(1)A(1,0,0),B(0,1,0) (2)A(1,2,1),B(0,2,-1)
(3)A(2,2,1),B(2,3,-1)(4)A(1,2,-3),B(-1,2,0)
5.求点A（5，-1，1）与z轴、y轴和x轴的距离.
6.求顶点为A（-1，1，4），B（2，-1，2），C（4，0，7）的三角形各边长.
9.证明：三角形的中位线平行于底边且等于底边的一半.
有关高等数学基础的文章
- 详细阅读
-
向量空间中的对偶向量都有对应的镜像详细阅读
所有能定义在V上的线性泛函的集合，构成了一个与V采用同样标量集的向量空间，我们将它写作V*。事实上，在抽象代数意义上，V*和V是同构的。因此，我们称这些线性泛函为对偶向量或者余向量，称V*为对偶空间。构造对偶空间V*的对偶空间V(**)，我们又会回到V，因此，V和V*就很像是彼此的镜像。每一个向量空间都有它的对偶空间，如果其中一个发生反变转换，那么另一个会发生共变转换，反之亦然。......
2023-11-22
- 详细阅读
-
目标的向量空间表示模型方案介绍详细阅读
一个目标在上述约定下可以看成是n维空间中的一个向量，这就是向量空间模型的由来。下面结合目标的表示，给出其定义。，td}；2）依据目标特征项序列，对训练集和测试集中的各个目标样本进行权重赋值、规范化等处理，将其转化为机器学习算法所需的模式向量。图6-2 目标的向量空间模型示意图......
2023-06-28
-
线性子空间的生成与向量组的等价性详细阅读
，βt）.进一步有，等价的向量组生成相同的线性子空间.命例4.9 对任意一个向量组α1，α2，…，αs}.这两个命题的证明留作习题.定理4.7 若W是n维线性空间V的子空间，则对W的任意一组基α1，α2，…......
2023-11-22
-
平面直角坐标系中的位似变换探讨详细阅读
在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点（x，y）对应的位似图形上的点的坐标为_________．1．在平面直角坐标系中，△ABC与△A′B′C′是以原点为位似中心的位似图形，若点A和它的对应点A′的坐标分别为（－4，2），（8，－4），则△ABC与△A′B′C′的相似比是（ ）．2．如图，△ABC和△A′B′C′位似，位似......
2023-07-03
-
学前儿童空间方位概念教育指导详细阅读
而儿童认识空间方位是以自己的身体为出发点，并在实际的动作中试验、理解自己与物体之间、物体与物体之间的空间关系。思考与练习1.运用学前儿童空间方位的知识，谈谈怎样组织和指导幼儿的建构区活动。研究者认为，根据这一实验结果，在幼儿的几何空间学习过程中，应当重视幼儿园的积木区，结合积木建构游戏，将绘本情境搭建方式融入教学中，以帮助幼儿更好地掌握空间方位的知识。......
2023-07-30
-
连续性方程在直角坐标系中的应用详细阅读
欧拉连续性方程是欧拉在1755年建立的。按欧拉方法，如图1.12所示，首先选取控制体元——固定在空间上的一个确定的、形状任意的封闭体积，位置保持不变。控制体元可以非常小，如小到前文所述的特征体元；或者有限大，这需要根据研究问题所确定。控制体元的形状不会影响所得到的方程。ρv也称质量速度，它是单位时间内通过单位面积的流体质量。......
2023-06-28
相关推荐