一、不定积分的概念原函数定义：设f（x）是定义某区间I上的已知函数，若存在一个函数F（x），对于该区间上每一点都满足：F′（x）=f（x）或dF（x）=f（x）dx，则称F（x）是f（x）在该区间I上的一个原函数.如已知f（x）=2x，由于F（x）=x2满足F′（x）=（x2）′=2x，所以F（x）=x2是f（x）=2x的一个原函数.同理，x2+1，x2-1，x2+10等也都是f（x）=2x的原函......
2025-09-30
高等数学基础：定积分在几何上的应用
【摘要】：一、定积分的元素法（微元法）在定积分的应用中，人们经常采用所谓的元素法，为此，回顾一下之前讨论过的曲边梯形的面积计算方法.设f在区间[a，b]上连续，且f≥0，求以曲线y=f为曲边，底为[a，b]的曲边梯形的面积A，如图5.9所示.图5.9（一）分割用任意一组分点a=x0＜x1＜…
一、定积分的元素法（微元法）
在定积分的应用中，人们经常采用所谓的元素法，为此，回顾一下之前讨论过的曲边梯形的面积计算方法.
设f（x）在区间[a，b]上连续，且f（x）≥0，求以曲线y=f（x）为曲边，底为[a，b]的曲边梯形的面积A，如图5.9所示.
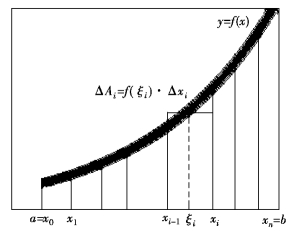
图5.9
（一）分割
用任意一组分点a=x0＜x1＜…＜xi-1＜xi＜…＜xn=b将区间分成n个小区间[xi-1，xi]，其长度为
（二）近似替代
曲边梯形被划分成n个小曲边梯形，每一小曲边梯形被分成小矩形，第i个小矩形的面积记为ΔAi（i=1，2，…，n），则
（三）求和
得面积的近似值
（四）求极限
得面积A的精确值
为了保证所有小区间的长度都无限缩小，要求小区间长度中的最大值趋于零，即
由上述过程可见，（二），（四）两步最重要，通过对求曲边梯形面积问题的回顾、分析、提炼，可以给出用定积分计算某个量的条件与步骤.
计算A的定积分表达式步骤如下所述.
（1）选取一个变量x为积分变量，在[a，b]中任取一微元区间[x，x+dx]；
（2）求微元dA=f（x）dx；
二、定积分在几何上的应用
（一）直角坐标系下平面图形的面积
由曲线y=f（x）（f（x）≥0）及直线x=a与x=b（a＜b）与x轴所围成的曲边梯形面积A，如图5.10所示.
一般来说，由曲线y=f（x）与y=g（x）及直线x=a，x=b（a＜b）所围成的图形面积A，如图5.11所示.
图5.10
图5.11
【例题1】 求由y=x2，x=2及x轴所围成图形的面积，如图5.12所示.
图5.12
解：如图5.12所示，所围图形就是曲边梯形OAB，选取一个变量x为积分变量，在[0，2]任取其中的一微元区间[x，x+dx]，则dA=x2dx，
【例题2】 求由抛物线y=x2与直线y=x所围成的图形面积.
选x为积分变量，则x的变化范围是[0，1]，任取其上的一个区间微元[x，x+Δx]，则可得到相应于[x，x+Δx]的面积微元
从而所求面积为
【例题3】 求由y2=x，y=x2所围成图形的面积.
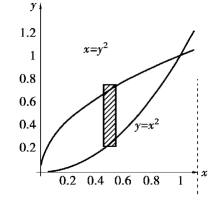(https://www.chuimin.cn)
图5.13
图5.14
（二）旋转体的体积
旋转体是由一个平面图形绕该平面内一条定直线旋转一周而生成的立体图形，该定直线称为旋转轴.
计算由曲线y=f（x），直线x=a，x=b及x轴所围成的曲边梯形，绕x轴旋转一周而生成的立体的体积.
根据微元法，解法步骤如下：
（1）取x为积分变量，则x∈[a，b]，对于区间[a，b]上的任一区间[x，x+dx]，它所对应的曲边梯形绕x轴旋转而生成的薄片似的立体的体积近似等于以f（x）为底半径，dx为高的圆柱体的体积.
（2）体积元素为dV=π[f（x）]2dx.
图5.15
取x为积分变量，则体积元素为
习题5.5
1.计算由下列曲线所围成的图形的面积
（1）y=x，x=2，x轴
（2）y=x2，x=2，x轴
（3）y=ex，x=1，x轴，y轴
（4）y=x2（x≥0），y=2，y轴
(6)y=x2,x+y=2
(7)y=x2,y=x
(8)y=2x-x2,x+y=0
2.计算由下列曲线所围成的平面图形绕指定轴旋转而成的旋转体的体积
（1）y=x，x=1，x轴；绕x轴
（2）y=x2，x=1，x轴；绕x轴
（3）y=ex，x=2，x轴，y轴；绕x轴
（5）y=sinx，x∈[0，π]，x轴；绕x轴
（6）x2+y2=1（x＞0，y＞0）；绕x轴
复习题五
一、填空题
二、选择题
三、计算题
四、应用题
1.计算由抛物线y=ex，x=1及x轴，y轴所围图形的面积.
2.计算由抛物线y=x2（x≥0），x=3及x轴所围图形的面积.
3.计算由y=2x，x=1及x轴所围成的平面图形绕x轴旋转而成的旋转体的体积.
4.计算由y=x2，x=2及x轴所围成的平面图形绕x轴旋转而成的旋转体的体积.
天才数学家——欧拉
相关文章
- 详细阅读
- 详细阅读
- 详细阅读
-
高等数学上册：定积分的元素法详细阅读
为总结出定积分应用的一般思想和方法，我们先回顾一下用定积分求曲边梯形面积问题的方法和步骤.设f在区间［a，b］上连续，且f≥0，求以曲线y＝f为曲边的［a，b］上的曲边梯形的面积A.把这个面积A表示为定积分的思路是“分割、取近似、求和、取极限”，具体步骤是：图6－1分割：将［a，b］分成n个小区间，相应地把曲边梯形分成n个小曲边梯形，其面积记作ΔAi（i＝1，2，…......
2025-09-30
-
高等数学上册：定积分换元法详细阅读
定理1设函数f（x）在［a，b］上连续，函数x＝φ（t）满足条件：（1）φ（α）＝a，φ（β）＝b，且a≤φ（t）≤b.（2）φ（t）在［α，β］（或［β，α］）上有连续导数.则有公式（5－5）称为定积分的换元公式.证由于f（x）在［a，b］上连续，则存在原函数，在［a，b］上可积.设F′（x）＝f（x），则又｛F［φ（t）］｝′＝F′［φ（t）］·φ′（t）＝f［φ（t）］·φ′（t），于是......
2025-09-30
-
高等数学学习指导：第四章定积分及应用详细阅读
知识要点一、定积分的概念及性质1.定积分的定义：设函数f（x）是定义在区间［a，b］上连续函数，经过分割、近似替代，求和及取极限的方法求曲边梯形的面积，记作为2.定积分的几何意义：当f（x）≥0时表示由y=f（x），x=a，x=b与x轴围成的曲边梯形的面积A.如果f（x）≤0时，由于，于是表示曲边梯形面积的相反数，即.如果f（x）在［a，b］上有时为正，有时为负，则等于各部分面积的代数和.3.定积......
2025-09-30
-
如何求不定积分-高等数学上册详细阅读
定义2若F（x）是f（x）在区间I上的一个原函数，则称F（x）＋C为f（x）在区间I上的不定积分，记作即∫f（x）dx＝F（x）＋C其中C为任意常数，记号“∫”称为积分号，f（x）称为被积函数，f（x）dx称为被积表达式，x称为积分变量.由定义2可知，求的关键就是求出f（x）的一个原函数，不定积分与原函数是总体与个体的关系.由此，本节开头所举的两个例子可写作从不定积分的定义即可知下述关系：或又由......
2025-09-30
-
染料固着在纤维上的过程优化方案详细阅读
染料在纤维上的固着是上染的最后阶段，它对染色牢度影响很大。染料在纤维上的固着，主要通过库仑力、范德瓦尔斯力、氢键、共价键、配位键等。因此在染料分子与纤维分子形成氢键的同时，原有的氢键将发生断裂。氢键的能量、作用半径都和范德瓦尔斯力的能量、作用半径属于一个数量级，染料和纤维分子中一般都含有供氢和吸氢基团，因此氢键也普遍存在于各纤维染色体系中。......
2025-09-29
相关推荐