一、函数的有界性如果对属于某一区间I的所有x值总有│f（x）│≤M成立，其中M是一个与x无关的常数，那么我们就称f（x）在区间I有界，否则便称无界.注：一个函数，如果在其整个定义域内有界，则称为有界函数.例如：函数y=cosx在（-∞，+∞）内是有界的.再如：当x∈（-∞，+∞）时，恒有|sinx|≤1，所以函数f（x）=sinx在（-∞，+∞）内是有界函数.这里M=1（当然，也可以取大于1的任何......
2025-09-30
高等数学基础:函数图形描绘方法大揭秘
【摘要】：3.已知x+y=4，运用极值第二定理证明：当x=y时，L=x2+y2有最小值.
一、函数的渐近线
定义 当曲线y=f（x）上的一动点P沿着曲线移向无穷远时，如果点P到某指定直线L的距离趋近于零，那么直线L就称为曲线y=f（x）的一条渐近线.
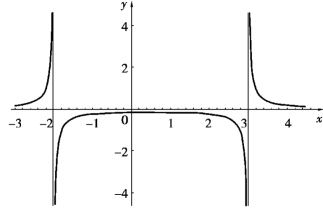
图3.7
有垂直渐近线两条：x=-2，x=3
（二）水平渐近线（平行于x轴的渐近线）
那么y=b就是y=f（x）的一条水平渐近线.
例如y=arctanx，
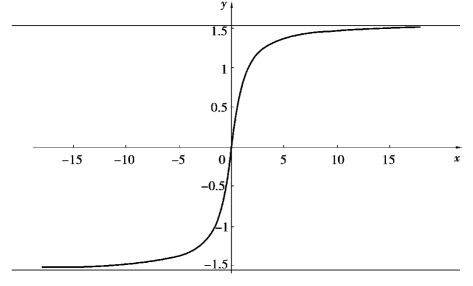
图3.8
（三）斜渐近线
那么y=ax+b就是y=f（x）的一条斜渐近线.
斜渐近线的求法：
二、函数图形描绘的步骤和方法
（一）步骤
利用函数特性描绘函数图形.
（1）确定函数y=f（x）的定义域，对函数进行奇偶性、周期性、曲线与坐标轴交点等性态的讨论，求出函数的一阶导数f′（x）和二阶导数f″（x）.
（2）求出方程f′（x）=0和f″（x）=0在函数定义域内的全部实根，用这些根同函数的间断点或导数不存在的点把函数的定义域划分成几个部分区间.
（3）确定在这些部分区间内f′（x）和f″（x）的符号，并由此确定函数.
（4）确定函数图形的水平、垂直渐近线、斜渐近线以及其他变化趋势.
（5）描出与方程f′（x）=0和f″（x）=0的根对应的曲线上的点，有时还需要补充一些点，再综合前述步骤讨论的结果画出函数的图形.
（二）作图举例
【例题3】 描绘方程（x-3）2+4y-4xy=0的图形.
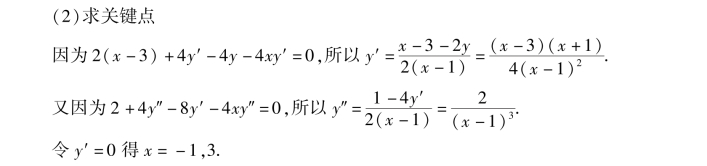
（3）判别曲线形态
（4）求渐近线
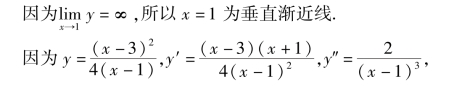
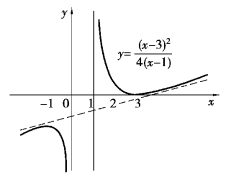
图3.9
令f′（x）=0，得x=-2；令f″（x）=0，得x=-3.
（3）判别曲线形态
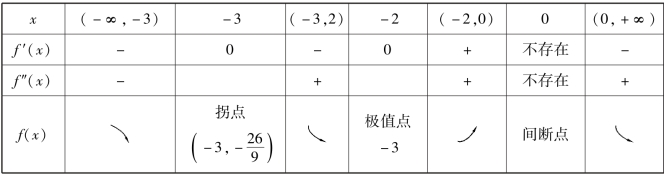
（4）求渐近线
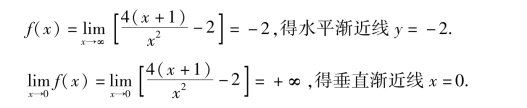
（5）绘图
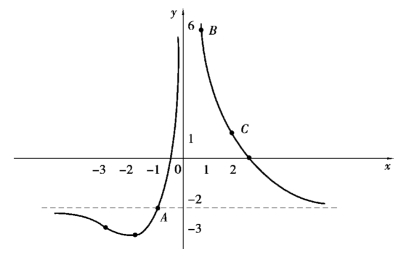
图3.10
习题3.5(https://www.chuimin.cn)
1.判断题.
（1）每一条曲线都有渐近线.（ ）
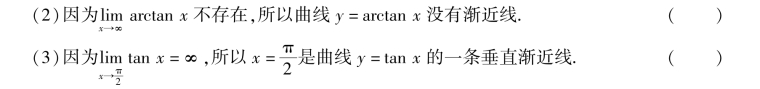
2.填空题.
3.选择题.
（2）设曲线y=lnx，则x=0是曲线的（ ）.
A.水平渐近线 B.垂直渐近线 C.极值点 D.驻点
A.x=0 B.x=-e-1C.x=e-1D.x=lne-1
4.作出下列函数的图像：
复习题三
一、填空题
1.函数y=x2-1在[-1，2]上满足拉格朗日中值定理的ξ____________________.
2.函数f（x）=x3-3x的驻点为_________________.
3.函数f（x）=x2-2x+1的单增区间为_________________.
4.函数f（x）=x2-2x在[0，2]上的最大值为_________________.
5.函数y=x3-1的拐点为_________________.
二、选择题
1.若x=1是f（x）=x2-ax+1的驻点，则a=（ ）.
A.0 B.1 C.2 D.3
2.若函数f（x）在（a，b）内二阶可导，且f′（x）＜0，f″（x）＜0，则在（a，b）内函数（ ）.
A.单调增加，向上凸 B.单调减少，向上凸；
C.单调增加，向上凹 D.单调减少，向上凹
3.曲线y=x3-3x2+6的拐点是（ ）.
A.x=1 B.(1,4) C.x=0 D.(4,1)
4.函数f（x）=x2-4x在[0，3]最小值为（ ）.
A.0 B.2 C.3 D.-3
5.f（x）=x3-3x在定义域R上的极大值为（ ）.
A.-1 B.1 C.-2 D.2
三、计算题
1.求函数的单调区间和极值.
(1)f(x)=x2-2x; (2)f(x)=x3-12x.
2.求下列函数的最值.
(1)f(x)=x2-2x+1,x∈[0,2]; (2)f(x)=x3-3x+1,x∈[-2,2].
3.求函数f（x）=x4-2x2的凹凸区间和拐点.
4.运用洛必达法则求极限.
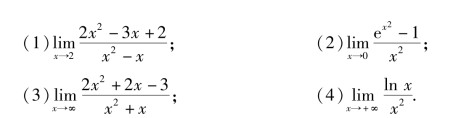
四、应用题
1.若点（1，2）是曲线y=ax3+bx2+4x的拐点，求a， B.
2.一根铁丝长64m，靠墙围成一个矩形的篱笆，问长、宽取何值时，矩形篱笆围成的面积最大？
3.已知x+y=4，运用极值第二定理证明：当x=y时，L（x）=x2+y2有最小值.
相关文章
- 详细阅读
-
基本初等函数-高等数学基础详细阅读
一、基本初等函数我们常用的基本初等函数有6种，分别是常数函数、指数函数、对数函数、幂函数、三角函数及反三角函数.（一）常数函数y=c（c为常数）.（二）幂函数1.函数y=xα称为幂函数，其中x是自变量，α是常数.2.幂函数的性质及图像的变化规律①所有的幂函数在（0，+∞）都有定义，并且图像都过点（1，1）.图1.9②α＞0时，幂函数的图像通过原点和点（1，1），并且在区间[0，+∞）上是增函数.③......
2025-09-30
-
高等数学基础：连续函数概念及示例详细阅读
一、连续函数的概念在自然界中有许多现象都是连续不断地变化的，如，气温随着时间的变化而连续变化；金属轴的长度随气温有极微小的改变也是连续变化的等.这些现象反映在数量关系上就是我们所说的连续性.函数的连续性反映在几何上可以看作一条不间断的曲线；下面给出连续函数的概念.（一）函数的增量增量的定义，简单说，就是变化后的量减去变化前的量.例如：早晨t1=8时，温度T1=2℃，中午t2=14时，温度T2=12......
2025-09-30
-
教师儿童研究方法大揭秘详细阅读
上一章中的叙事性描述强调的是具体性和叙说性，尽管轶事记录可以就某位儿童记录一段时间的轶事，但轶事记录最重要的是强调轶事性，历时性强调的是对儿童描述的持续性和动态性，就像上述两位研究者对科沙纳所做的历经一年多的研究，本质上是对儿童的发展研究，据此，本章主要讨论历时性的描述方法。历时性描述就是把现象自己“说”出来的、显现出来的东西动态、持续地记录下来。......
2025-09-29
-
高等数学基础：中值定理和函数单调性详细阅读
一、拉格朗日（Lagrange）中值定理定理1（拉格朗日中值定理）若函数f（x）满足条件：（1）在闭区间[a，b]上连续；（2）在开区间（a，b）内可导；则至少存在一点ξ∈（a，b），使得或图3.1拉格朗日中值定理的几何意义：如果在闭区间[a，b]上连续的一条曲线弧y=f（x）除端点外处处具有不垂直于x轴的切线，则曲线上至少存在一点C，使得曲线在点C处的切线平行于连接曲线两端点的弦AB.显然，......
2025-09-30
-
辣椒碱的测试方法大揭秘，详细阅读
在实际测试中，可用单一的辣椒素作标样来定性和定量其他各个辣椒碱。把所有的结果相加即为辣椒总碱的含量。测试步骤①标准液的配制：称取10 mg辣椒素，转入100 m L容量瓶中，加甲醇溶解，定容，摇匀。若样品是辣椒或辣椒粉，称取相当于含有10 mg辣椒素的样品，转入200 mL容量瓶中，加入90 m L醋酸钠饱和了的95%乙醇溶液，放入60℃水浴中，用磁棒搅拌5 h。......
2025-09-29
-
多目标问题求解方法大揭秘详细阅读
权重和法可表示为权重可以看作决策者对于目标函数的偏好，即多目标之间的相对重要性。在实际应用中，往往准确的权重或各目标之间优先级很难获得，如果无法获得对目标函数的先验偏好信息，就只能采用产生式方法来求解问题以获得Pareto最优解集。由于产生式方法在优化过程中产生了较多的Pareto最优解，在处理高维目标优化问题时，其选择无法直接表明，导致计算代价过大。图9-3多目标优化求解策略示意......
2025-09-29
-
并列式论述观点方法大揭秘详细阅读
所谓“并列式”，就是围绕一个话题，分别从几个方面展开论述。当然，所谓“并列”也是相对的，几个小论点之间可能也有主次之分。二是建立“特殊学生档案”。......
2025-09-30
相关推荐