并求此时曲线的凹凸区间.解y″＝12ax2＋6bx由于点（1，3）在该曲线上，将点（1，3）代入该曲线方程中得a＋b＝3又点（1，3）为曲线的拐点，故解得a＝－3，b＝6.此时y″＝－36x2＋36x＝36，由y″＝36＝0，解得x1＝0，x2＝1.列表表示如下.表3－3由表3－3可知，曲线的凸区间为，曲线的凹区间为［0，1］.利用凹凸性可以证明一类特殊的不等式.例8证明证取所以在上，曲线f＝tant是凹的.因此当时，有即......
2023-11-19
高等数学基础：曲线凹凸和拐点
【摘要】：一、曲线凹凸性的定义为了较准确地描述函数的图形，仅知道函数的单调区间和极值是不行的，比如说，f（x）在[a，b]上单调，这时会出现图3.6中的几种情况，l1是一段凸弧，l2是一段凹弧，l3既有凸的部分，也有凹的部分，曲线具有这种凸和凹的性质，称为凸凹性.图3.6曲线的凸凹性从几何意义上看，凸弧具有这种特点：从中任取两点，连接此两点的弦总在曲线的下方.进而不难知道，在[a，b]中任意取两个点函数在
一、曲线凹凸性的定义
为了较准确地描述函数的图形，仅知道函数的单调区间和极值是不行的，比如说，f（x）在[a，b]上单调，这时会出现图3.6中的几种情况，l1是一段凸弧，l2是一段凹弧，l3既有凸的部分，也有凹的部分，曲线具有这种凸和凹的性质，称为凸凹性.
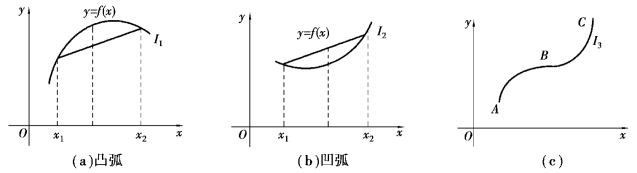
图3.6 曲线的凸凹性
从几何意义上看，凸弧具有这种特点：从中任取两点，连接此两点的弦总在曲线的下方.进而不难知道，在[a，b]中任意取两个点函数在这两点处的函数值的平均值小于这两点的中点处的函数值.凹弧也有相仿的特点.
定义 设f（x）在[a，b]上连续，若对∀x1，x2∈（a，b）恒有
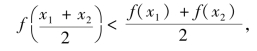
那么称f（x）在[a，b]上的图形是（向上）凹的或凹弧；如果恒有
那么称f（x）在[a，b]上的图形是（向下）凸的或凸弧.
如果f（x）在[a，b]上连续，且在（a，b）内的图形是凹的（或凸的），那么称为f（x）在[a，b]上的图形是凹的（或凸的）.
二、曲线凹凸性的判定
如果f（x）在[a，b]内具有二阶导数，那么可以利用二阶导数的符号来判定曲线的凹凸性，这就是下面的曲线凹凸性的判定定理.
定理1 设f（x）在[a，b]上连续，在（a，b）内具有一阶和二阶导数.
（1）若在（a，b）内，f″（x）＜0，则f（x）在[a，b]上的图形是凸的.
（2）若在（a，b）内，f″（x）＞0，则f（x）在[a，b]上的图形是凹的.
拐点：连续曲线y=f（x）上凹弧与凸弧的分界点称为该曲线的拐点.
定理2 如果f（x）在（x0-δ，x0+δ）内存在二阶导数，则点[x0，f（x0）]是拐点的必要条件是f″（x0）=0.
确定曲线y=f（x）的凹凸区间和拐点的步骤：
（1）确定函数y=f（x）的定义域；
（2）求出二阶导数f″（x）；
（3）求使二阶导数为零的点和使二阶导数不存在的点；
（4）判断或列表判断，确定曲线凹凸区间和拐点；
【例题1】 判别曲线y=2x2+3x+1的凹凸性.
解：因为y′=4x+3，y″=4＞0，
所以曲线y=2x2+3x+1在其定义域（-∞，+∞）上是凹的.
【例题2】 判别曲线y=x3的凹凸性.
解：因为y′=3x2，y″=6x.
当x＜0时，y″＜0，曲线在（-∞，0]是凸的；(www.chuimin.cn)
当x＞0时，y″＞0，曲线在[0，+∞）是凹的.
注意到，点（0，0）是曲线由凸变凹的分界点.
【例题3】 求y=xe-x的拐点.
解：y′=（1-x）e-x，y″=（x-2）e-x，令y″=0⇒x=2.
当x＜2时，y″＜0；当x＞2时，y″＞0.
所以x=2为拐点.
列表讨论：
习题3.4
1.填空题
（1）若点（1，2）是曲线y=ax3+bx2+4x的拐点，则a=________，b=________.
（2）曲线y=xex的凹区间是_________，凸区间是_________，拐点是_________.
2.选择题
（1）曲线y=x3-3x2+3在区间（-∞，-1）和（-1，1）内分别为（ ）.
A.凸的，凸的 B.凸的，凹的
C.凹的，凸的 D.凹的，凹的
（2）曲线y=lnx+1在区间（0，1）和（1，2）内分别为（ ）.
A.凸的，凸的 B.凸的，凹的
C.凹的，凸的 D.凹的，凹的
（3）曲线y=e-x区间（-1，0）和（0，1）内分别为（ ）.
A.凸的，凸的 B.凸的，凹的
C.凹的，凸的 D.凹的，凹的
3.计算题
（1）求曲线y=x3-1的凹凸区间.
（2）求曲线y=xex的凹凸区间和拐点.
（3）求曲线y=x4-2x3+1的凹凸区间和拐点.
（4）a、b为何值时，点（1，3）为曲线y=ax3+bx2的拐点？
有关高等数学基础的文章
- 详细阅读
-
曲线凹凸性、拐点计算：全面复习与解析详细阅读
1.曲线凹凸性及其判定方法在某个区间内，如果曲线位于其上任意一点的切线的上方（下方），则称曲线在该区间内为凹的（凸的）.曲线y=f（x）在区间I上凹凸性的判定方法是：设函数f（x）在I上二阶可导.如果f″（x）>0（x∈I），则曲线y=f（x）在I上是凹的；如果f″（x）<0（x∈I），则曲线y=f（x）在I上是凸的.2.曲线拐点及其计算方法设函数f（x）连续，则曲线y=f（x）上的凹弧与凸弧的分......
2023-10-27
-
高等数学：函数单调性和凹凸性详细阅读
一、函数的单调性从图上可以直观地看出，单调增加函数的切线斜率非负（见图3-3），单调减少函数的切线斜率非正（见图3-4）.图3-3图3-4定理3.7 设函数f（x）在区间I内可导，则：1）对任意x∈I，有f′（x）＞0，则函数f（x）在I严格单调增加；2）对任意x∈I，有f′（x）＜0，则函数f（x）在I严格单调减少.证 先证1）对任意x1，x2∈I且x1＜x2，函数f（x）在区间[x1，x2]上......
2023-11-22
-
高等数学基础：曲面和曲线介绍详细阅读
在上节，我们已经介绍了曲面及曲面方程的概念.如果曲面Σ上每一点的坐标都满足方程F（x，y，z）=0，而不在曲面Σ上的每一点坐标都不满足方程F（x，y，z）=0，则称方程F（x，y，z）=0为曲面方程，称曲面Σ为F（x，y，z）=0的图形.在空间直角坐标系中，如果F（x，y，z）=0是二次方程，则它的图形称为二次曲面.下面给出几种常见的曲面方程，如下所述.一、球面方程空间一动点到定点的距离为定值，该......
2023-11-20
-
函数的极值和最值-高等数学基础详细阅读
解：要使材料最省，就是要罐头筒的总表面积最小.设罐头的底半径为r，高为h，如图3.5所示，则它的侧面积为2πrh，底面积为πr2，因此总表面积为图3.5于是得出结论：当所做罐头筒的高和底直径相等时，所用材料最省.习题3.21.求函数的单调区间和极值.f=x2-2x+4;f=x2-6x;y=2x3-3x2;y=x-ln(1+x);f=x3-12x.2.运用极值的第二定理求极值.f=x2-2x;f=x4-2x2.3.求函数的最值.f=x2-2x+1,x∈[-1,2];f=x2-2x,x∈[0,2];f=x3-3x,x∈[0,2];f=x4-2x2,x∈[0,2].4.已知x+y=s，运用极值第二定理证明......
2023-11-20
-
高等数学基础：中值定理和函数单调性详细阅读
一、拉格朗日（Lagrange）中值定理定理1（拉格朗日中值定理）若函数f（x）满足条件：（1）在闭区间[a，b]上连续；（2）在开区间（a，b）内可导；则至少存在一点ξ∈（a，b），使得或图3.1拉格朗日中值定理的几何意义：如果在闭区间[a，b]上连续的一条曲线弧y=f（x）除端点外处处具有不垂直于x轴的切线，则曲线上至少存在一点C，使得曲线在点C处的切线平行于连接曲线两端点的弦AB.显然，......
2023-11-20
-
MATLAB简介|高等数学基础详细阅读
，xn，yn，选项n）画y=cosx的图像，并用蓝色，点画线，五角星标注.clearclcx=0：0.02：2*piy=cosplot·画y=x^3图像，用黑色、实线、星号表示.·clear·clcx=0：0.2：5·y=x.^3·plotholdon/off命令控制是保持原有图形还是刷新原有图形，不带参数的hold命令在两种状态之间进行切换.绘制分段函数程序如下：x=-10：0.1：0y=x.^2plot(x,y)holdonx=0：0.1：10y=x.^3plot(x,y)练习一1.谈谈你对MATLAB的认识.2.绘制y=sin2x在[0，2π]范围内的图像.3.绘制y=x3cosx的图像用蓝色、实线、三角形标注（要求写出语句，......
2023-11-20
-
《高等数学基础》MATLAB：积分求解详细阅读
一、求积分求积分由函数int来实现.该函数的一般调用格式为：int（s）：没有指定积分变量和积分阶数时，系统按默认变量对被积函数或符号表达式s求不定积分.int（s，v）：以v为自变量，对被积函数或符号表达式s求不定积分.int（s，v，a，b）：求定积分运算.a，b分别表示定积分的下限和上限.该函数求被积函数在区间[a，b]上的定积分.a和b可以是两个具体的数，也可以是一个符号表达式，还可以是无......
2023-11-20
相关推荐