函数的极值和最值-高等数学基础

2023-11-20 理论教育版权反馈

【摘要】：解：要使材料最省，就是要罐头筒的总表面积最小.设罐头的底半径为r，高为h，如图3.5所示，则它的侧面积为2πrh，底面积为πr2，因此总表面积为图3.5于是得出结论：当所做罐头筒的高和底直径相等时，所用材料最省.习题3.21.求函数的单调区间和极值.f=x2-2x+4;f=x2-6x;y=2x3-3x2;y=x-ln(1+x);f=x3-12x.2.运用极值的第二定理求极值.f=x2-2x;f=x4-2x2.3.求函数的最值.f=x2-2x+1,x∈[-1,2];f=x2-2x,x∈[0,2];f=x3-3x,x∈[0,2];f=x4-2x2,x∈[0,2].4.已知x+y=s，运用极值第二定理证明

一、函数的极值

（一）极值的定义

如图3.4所示，观察函数y=f（x）在点x1、x2、x3、x4处的函数值f（x1）、f（x2）、f（x3）、f（x4），与它们左右近旁各点处的函数值相比有什么特点？

设y=f（x）在x0的一个邻域内有定义，且除x0外，

（1）恒有f（x）＜f（x0），则称f（x0）为f（x）的极大值，点x0称为f（x）的一个极大值点；

（2）恒有f（x）＞f（x0），则称f（x0）为f（x）的极小值，点x0称为f（x）的一个极小值点.

函数的极大值与极小值统称为极值，使函数取得极值的点称为极值点.

显然，极值是一个局部的概念，它与极值点邻近的所有点的函数值相比较而言，并不意味着它在函数的整个定义域内最大或最小.

定理　（极值存在的必要条件）：若点x0是函数f（x）的极值点，且x0处的函数可微，则f′（x0）=0.称f′（x0）=0的点为函数的驻点.例如函数y=x3，x=0是函数的驻点，但函数在（-∞，+∞）内单调增加，x=0不是极值点.由此可得出：f（x）的驻点不一定是极值点.

下面我们给出极值判断的条件.

（二）极值的第一判定定理

设函数f（x）在点x0的某δ邻域内连续且可导.

（1）若当x＜x0时，f′（x）＞0，则，当x＞x0时，f′（x）＜0，则f（x0）为极大值；

（2）若当x＜x0时，f′（x）＜0，当x＞x0时，f′（x）＞0，则f（x0）为极小值；

（3）若当x≠x0时，恒有f′（x）＜0或f′（x）＞0，则f（x）在x0处没有极值.

也就是说，当x在该邻域内由小增大经过x0时，如果f′（x）由正变负，那么x0是f（x）的极大值点，f（x0）是f（x）的极大值；f′（x）由负变正，那么x0是f（x）的极小值点，f（x0）是f（x）的极小值；f′（x）不改变符号，那么x0不是f（x）的极值点.

求函数y=f（x）单调性和极值的步骤.

（1）确定函数的y=f（x）定义域，如为R；

（2）求f′（x）；

（3）f′（x）=0，求出函数f（x）在定义域内导数为零的点和不可导点，如为x1，x2；

（4）区间划分

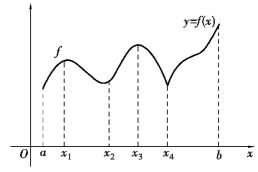
pagenumber_ebook=67,pagenumber_book=59

图3.4

【例题1】　求函数f（x）=x2-2x-3的单调区间及极值.

解：（1）f（x）的定义域为R；

(2)f′(x)=2x-2;

（3）令f′（x）=0，得x=1；

（4）区间划分

pagenumber_ebook=68,pagenumber_book=60

【例题2】　求出函数f（x）=x3-3x2-9x+5的极值.

解：（1）函数的定义域为R；

(2)f′(x)=3x2-6x-9=3(x+1)(x-3);

（3）令f′（x）=0得x1=-1，x2=3[无f′（x）不存在的点]；

（4）区间划分，用x1=-1，x2=3作为界点将定义域分区列表得

pagenumber_ebook=68,pagenumber_book=60

（3）用x=0和2作为分界点将（-∞，+∞）分区列表，即可得极值和单调区间.

pagenumber_ebook=68,pagenumber_book=60

极大值为f（0）=0；极小值为f（2）=0.

（三）极值的第二充分条件

设函数f（x）在点x0的某一邻域内二阶可导，且f′（x）=0，f″（x）≠0，则：

（1）当f″（x0）＜0时，函数f（x）在x0处取得极大值；(www.chuimin.cn)

（2）当f″（x0）＞时，函数f（x）在x0处取得极小值.

【例题4】　求出函数f（x）=x3-3x2-9x+5的极值.

解：因为f′（x）=3x2-6x-9，f″（x）=6x-6，

令f′（x）=0得x1=-1，x2=3，

所以f″（-1）=-12＜0，故f（-1）=10为极大值；

f″（3）=12＞0，故f（3）=-22为极小值.

二、函数的最大值和最小值

在生产实践及科学实验中，常遇到“最好”“最省”“最低”“最大”和“最小”等问题.例如质量最好，用料最省，效益最高，成本最低，利润最大，投入最小等，这类问题在数学上常常归结为求函数的最大值或最小值问题.

（一）闭区间[a，b]上的最大值和最小值

如果函数f（x）在闭区间[a，b]上连续，则f（x）在[a，b]上必有最大值和最小值.连续函数在闭区间[a，b]上的最大值和最小值仅可能在区间内的极值点和区间的端点处取得.

求函数在区间内的最值的步骤：

（1）求出函数y=f（x）在（a，b）内的全部驻点和驻点处的函数值；

（2）求出区间端点处的函数值f（a），f（b）和不可导点的函数值；

（3）比较以上各函数值，其中最大的就是函数的最大值，最小的就是函数的最小值.

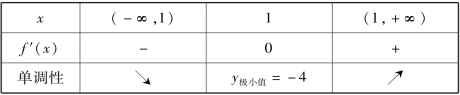
【例题5】　求函数f（x）=x2-2x-3在[0，2]的最值.

解：（1）f′（x）=2x-2；

（2）令f′（x）=0，得x=1

(3)f(1)=-4,f(0)=-3,f(2)=-3;

【例题6】　求函数f（x）=x3-3x+3，在区间[-3，1]的最大值、最小值.

解：f（x）在此区间处处可导，先来求函数的极值f′（x）=3x2-3=0，故x=±1，再来比较端点与极值点的函数值，取出最大值与最小值即为所求.因为f（1）=1，f（-3）=-15，f（-1）=5，故函数的最大值为f（-1）=5，函数的最小值为f（-3）=-15.

注　在实际应用中，若应满足连续且可导条件在一个区间内（开区间、闭区间或无穷区间）只有一个极大值点，而无极小值点，则该极大值点一定是最大值点.对于极小值点也可作出同样的结论.

（二）应用举例

【例题7】　要做一个容积为V的圆柱形罐头筒，怎样设计才能使所用材料最省？

解：要使材料最省，就是要罐头筒的总表面积最小.设罐头的底半径为r，高为h，如图3.5所示，则它的侧面积为2πrh，底面积为πr2，因此总表面积为

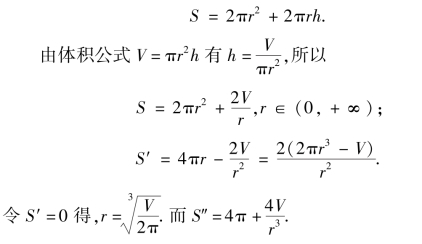
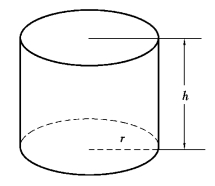
pagenumber_ebook=69,pagenumber_book=61

图3.5

pagenumber_ebook=69,pagenumber_book=61

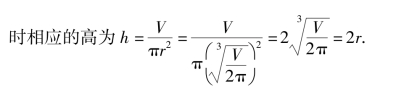
pagenumber_ebook=70,pagenumber_book=62

于是得出结论：当所做罐头筒的高和底直径相等时，所用材料最省.

习题3.2

1.求函数的单调区间和极值.

(1)f(x)=x2-2x+4;　(2)f(x)=x2-6x;

(3)y=2x3-3x2;　(4)y=x-ln(1+x);

(5)f(x)=x3-12x.

2.运用极值的第二定理求极值.

(1)f(x)=x2-2x;　(2)f(x)=x4-2x2.

3.求函数的最值.

(1)f(x)=x2-2x+1,x∈[-1,2];　(2)f(x)=x2-2x,x∈[0,2];

(3)f(x)=x3-3x,x∈[0,2];　(4)f(x)=x4-2x2,x∈[0,2].

4.已知x+y=s（s是定值），运用极值第二定理证明：当x=y时，L（x）=x2+y2有最小值.

函数的极值和最值-高等数学基础

相关推荐