首页理论教育函数微分原理:正方形金属薄片受温度变化影响导致面积变化

函数微分原理:正方形金属薄片受温度变化影响导致面积变化

2023-11-20 理论教育版权反馈

【摘要】：在学习函数的微分之前，我们先来分析一个具体问题：一块正方形金属薄片在受温度变化的影响时，其边长由x0变到了x0+Δx，则此薄片的面积改变了多少？

在学习函数的微分之前，我们先来分析一个具体问题：一块正方形金属薄片在受温度变化的影响时，其边长由x0变到了x0+Δx，则此薄片的面积改变了多少？

pagenumber_ebook=58,pagenumber_book=50

图2.2

pagenumber_ebook=58,pagenumber_book=50

由此可以发现，如果边长变化得很小时，面积的改变量可以近似用2x0Δx来代替.

由上例可以给出微分的数学定义，如下的所述.

一、函数微分的定义

设函数在某区间内有定义，x0及x0+Δx在这区间内，则函数的增量可表示为

其中o（Δx）是Δx的高阶无穷小，则称函数y=f（x）在点x0增量的近似值f′（x0）Δx为函数y=f（x）在点x0相应于自变量增量Δx的微分，记作dy：

由于自变量x的微分dx=（x）′Δx=Δx，为此函数f（x）在点x0处的微分又可记作

函数f（x）在某区间内每一点都可微，则称f（x）是该区间的可微函数，函数在任意一点的微分可记作

pagenumber_ebook=58,pagenumber_book=50

定理1　函数f（x）在点x0可微的充要条件是在点x0可导，即可微必可导.

【例题1】　求函数y=1+3x的微分.

解：dy=f′（x）dx=（1+3x）′dx=3dx.

【例题2】　求函数y=cos（4x-5）的微分.

解：dy=f′（x）dx=[cos（4x-5）]′dx=-4sin（4x-5）·dx.

pagenumber_ebook=59,pagenumber_book=51

【例题4】　求函数y=cos3（4x-5）的微分.

解：dy=f′（x）dx=[cos3（4x-5）]′dx=-3cos2（4x-5）·sin（4x-5）·4dx

=-12cos2(4x-5)·sin(4x-5)dx.

*二、微分形式不变性

什么是微分形式不变性呢？

设y=f（u），u=φ（x），则复合函数y=f[φ（x）]的微分为：

由于φ′（x）dx=du，故可将复合函数的微分写成

由此可见，不论u是自变量还是中间变量，y=f（u）的微分dy总可以用f′（u）与du的乘积来表示，我们把这一性质称为微分形式不变性.

*【例题5】　已知y=sin（2x+1），求dy.

解：将2x+1看作中间变量u，根据微分形式不变性，有

dy=d(sinu)=cosudu=cos(2x+1)d(2x+1)=cos(2x+1)·2dx=2cos(2x+1)dx.

三、基本初等函数的微分公式与微分的运算法则

（一）微分公式

通过上面的学习可以知道，微分与导数有着不可分割的联系，于是通过基本初等函数导数的公式可得出基本初等函数微分的公式，下面我们用表格（部分公式）来把基本初等函数的导数公式与微分公式对比一下：

表2.1　基本初等函数的导数公式与微分公式

pagenumber_ebook=59,pagenumber_book=51

（二）微分运算法则

由函数和、差、积、商的求导法则可推导出相应的微分法则.为了便于理解，下面我们用表格来将微分的运算法则与导数的运算法则进行对照（表2.2）.

表2.2　函数和、差、积、商的求导法则和微分法则

pagenumber_ebook=60,pagenumber_book=52

复合函数的微分法则就是前面我们学到的微分形式不变性，在此不再详述.

四、微分的应用

微分是表示函数增量的线性主部.计算函数的增量，有时比较困难，但计算微分则比较简单，为此我们用函数的微分来近似代替函数的增量，这就是微分在近似计算中的应用.

利用上式可求Δy的近似值，即：

(www.chuimin.cn)

另一方面　Δy=f（x0+Δx）-f（x0）≈f′（x0）Δx

则　f（x0+Δx）≈f（x0）+f′（x0）Δx

利用上述近似公式又可求Δy，f（x0+Δx）或f（x）的近似值.

pagenumber_ebook=60,pagenumber_book=52

【例题8】　有一批半径为1cm的球，为了提高球面的光洁度，要镀上一层铜，厚度定为0.01cm.请估计每只球需要用铜多少克（铜的密度是8.9g/cm3）.

解：先求出镀层的体积，再求出相应的质量.

因为镀层的体积等于两个球体体积之差ΔV，可用微分近似代替增量

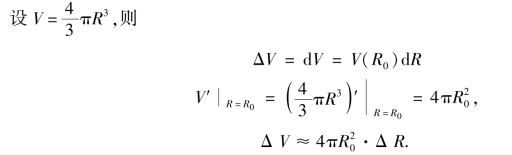
pagenumber_ebook=61,pagenumber_book=53

将R0=1，ΔR=0.01代入上式，得

于是镀每只球需要用的铜为　0.13×8.9=1.16（g）.

习题2.5

1.求下列函数的微分：

(1)y=x4-3x2-5x+6;　(2)y=x·cosx;

2.求下列函数的导数或微分：

(1)y=(3x-1)2;　(2)y=e2x+1;

(3)y=sin2x;　(4)y=cos(3x-1);

(5)y=cos22x;　(6)y=e(2x+1)2;

(7)y=sin2(2x+1)2;　(8)y=arccos(1-x).

pagenumber_ebook=61,pagenumber_book=53

复习题二

一、填空题

pagenumber_ebook=61,pagenumber_book=53

5.已知函数y=lnx，则y″=____________________.

二、选择题

1.已知函数f（x）=x3，则f′（x）=（　）.

A.1　B.2　C.3　D.4

2.曲线y=e2x在点（0，1）处切线的斜率是（　）.

A.1　B.–1　C.0　D.2

3.曲线y=x2-1上点M处的切线斜率是2，则点M的坐标是（　）.

A.(1,0)　B.(1,1)　C.(-1,0)　D.(-1,1)

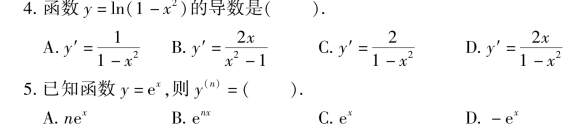
pagenumber_ebook=62,pagenumber_book=54

三、计算题

1.求下列函数的导数：

pagenumber_ebook=62,pagenumber_book=54

(7)y=(2x+1)3;　(8)y=cos(3x+1);

(9)y=sin22x;　(10)y=arccos(1-x).

2.求下列函数的微分：

(1)y=x4-x2-x;　(2)y=(3x-1)2;

(3)y=e2x+1;　(4)y=sin2(2x+1).

3.求下列隐函数的导数：

(1)x2+y2=4;.(2)x2+xy=4;

(3)x-ey=0.

四、应用题

1.求曲线y=x2+1上x=1处的切线方程和法线方程.

2.如果曲线y=x2+1的某一切线与直线y=2x平行，求切点坐标与切线方程.

pagenumber_ebook=62,pagenumber_book=54

微积分发展简史（二）