续表考点：导数在研究函数中的应用（2017全国I，21）已知函数f（x）=ae2x+（a-2）ex-x.（1）讨论f（x）的单调性；（2）若f（x）有两个零点，求a的取值范围.1.（2017山东莱芜二模）已知函数f（x）=ex[x2+（a+1）x+2a-1].（1）当a=-1时，求函数f（x）的单调区间；（2）若关于x的不等式f（x）≤ea在[a，+∞）上有解，求实数a的取值范围；（3）若曲线y=......
2025-09-30
导数的概念及物理学中的应用
【摘要】：一、导数的定义在学习导数的概念之前，我们先来讨论一下物理学中变速直线运动的瞬时速度的问题.（一）引例：速度问题设某点沿直线运动.设动点于时刻t在直线上的位移s=f（t），如果该点作匀速运动，则动点的速度为整个运动的平均速度.即：如果运动不是匀速的，那么在运动的不同时间间隔内，比值（1）会有不同的值.这样，把比值（1）笼统地称为该动点的速度就不合适了，而需要按不同的时刻来考虑.那么，这种非匀速运动的
一、导数的定义
在学习导数的概念之前，我们先来讨论一下物理学中变速直线运动的瞬时速度的问题.
（一）引例：速度问题
设某点沿直线运动.设动点于时刻t在直线上的位移s=f（t），如果该点作匀速运动，则动点的速度为整个运动的平均速度.
即：
如果运动不是匀速的，那么在运动的不同时间间隔内，比值（1）会有不同的值.这样，把比值（1）笼统地称为该动点的速度就不合适了，而需要按不同的时刻来考虑.那么，这种非匀速运动的动点在某一时刻（设为t0）的速度应如何理解而又如何求得呢？可以分为3步.
（1）在t0附近取一个小区间，设这一个小区间内时间的变化量为Δt，即时间从t0变化到t0+Δt，相应地在这段时间内，位移从s0=f（t0）变化到s=f（t0+Δt），即
（2）在这个小区间内动点的平均速度为
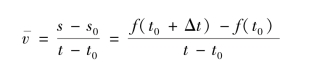
（3）如果时间间隔选得较短，这个平均速度近似于动点在时刻t0的速度.为了让平均速度等于时刻t0的速度，可以让小区间无限减小，即Δt→0，这样在t0点的速度就为v0，即：
这时就把这个极限值v0称为动点在时刻t0的（瞬时）速度.把上述引例加以归纳总结，就可以得出导数的定义.
（二）导数的定义
下面根据这3个步骤来求一些简单函数的导数.
【例题1】 用定义求函数y=3x2在x=1的导数.
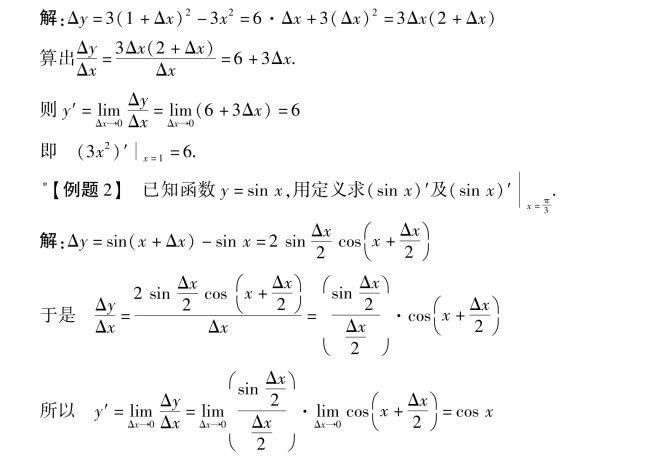
即：（sinx）′=cosx
若函数f（x）在区间（a，b）内每一点都可导，就称函数f（x）在区间（a，b）内可导.这时函数y=f（x）对于区间（a，b）内的每一个确定的x值，都对应着一个确定的导数，这就构成了一个新的函数，我们就称这个函数为原来函数y=f（x）的导函数.即：
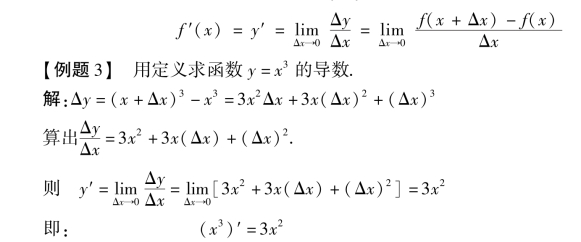
此结果对一般的幂函数y=xμ（μ为实数）均成立，即（xμ）′=μxμ-1.
【例题4】 用定义求函数y=logax（a＞0，a≠1）的导数.
由以上可归纳基本初等函数的导数公式如下：
（1）（c）′=0 （c为常数） （2）（xμ）′=μxμ-1
(5)(ax)′=ax·lna (6)(ex)′=ex
(7)(sinx)′=cosx (8)(cosx)′=-sinx
(9)(tanx)′=sec2x (10)(cotx)′=-csc2x
(11)(secx)′=tanxsecx (12)(cscx)′=-cotxcscx
【例题5】 利用导数公式求下列函数的导数.
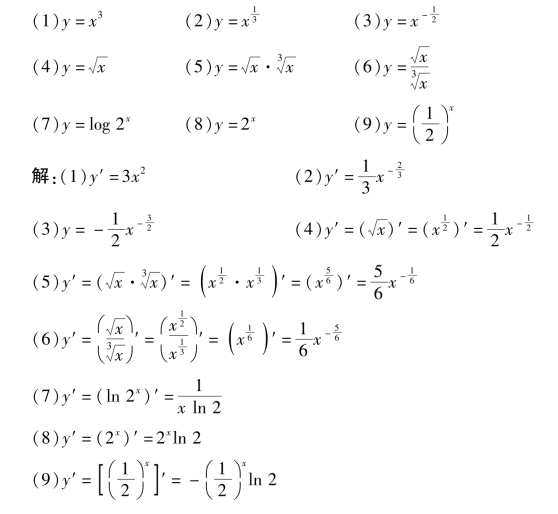(https://www.chuimin.cn)
二、导数的几何意义
【知识点回顾】
2.直线方程的5种形式
点斜式： y-y1=k（x-x1）
斜截式： y=kx+b
一般式： Ax+By+C=0
设M（x0，y0）是曲线C上的一个点（图2.1），则y0=f（x0）.在点M外另取C上的一点N（x，y），于是割线MN的斜率为
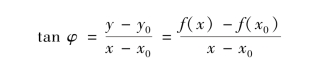
其中φ为割线MN的倾角.当点N沿曲线C趋于点M时，x→x0.如果当x→x0时，上式的极限存在，设为k，即
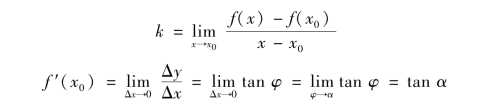
存在，则此极限k是割线斜率的极限，也就是切线的斜率.这里k=tanα，其中α是切线MT的倾角.
切线方程：y-y0=f′（x0）（x-x0）
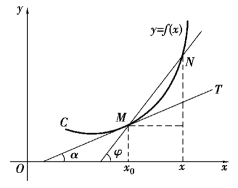
图2.1
所以切点为（1，-8）或（-1，-12）.
切线方程为y+8=4（x-1）或y+12=4（x+1），即
三、可导与连续的关系
前面已经介绍了左、右极限的概念，下面给出左、右导数的概念.
定理1 函数y=f（x）在x0处的可导的充分必要条件是函数y=f（x）在x0处的左右导数存在且相等.
定理2 可导必连续，连续未必可导.
习题2.1
1.利用导数的定义.
（1）求函数y=x在x=1处的导数；
（2）求函数y=x2的导数.
2.利用导数公式求下列函数的导数.
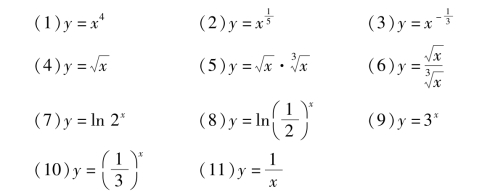
3.已知曲线y=x2上一点A（1，1），求：（1）过点A的切线的斜率；（2）过点A处的切线方程.
4.求曲线y=x2+1上x=1处的切线方程和法线方程.
5.如果曲线y=x2的某一切线与直线y=2x+3平行，求切点坐标与切线方程.
相关文章
- 详细阅读
-
DiffServ模型中的基本概念及应用详细阅读
DS域与DS区：DS域是一系列相连的DS节点构成的集合，这些节点遵循统一的服务提供策略并实现一致的PHB组。流量分类器的主要功能是依据每个数据包的DS值将其分类，以便根据SLA进行不同的调节和影射到一种或多种服务类型集合DSBA中，以在内部节点中接收不同等级的转发服务。PHB指对于某种DSBA，实际上是DiffServ网络节点给不同DSBA分配资源的方法，不同的PHB对应不同的缓冲区管理和分组调度机制。......
2025-09-30
-
直觉心理学：教育教学中的直觉应用详细阅读
本节从教师教学与学生学习两个方面来探讨直觉思维在教学中的应用。心理学的各学派的理论都认为直觉确实在学习中产生了非常大的作用。(二)直觉在学习中的有效运用学生作为学习的主体，在学习生涯中，更应该学会将直觉思维应用到学习生活中。结果发现大部分儿童会做出与成人相似的击打充气娃娃的行为。......
2025-09-30
-
学校心理学：智力概念的研究现状详细阅读
许多心理学家致力于智力的研究，但对智力的概念，心理学界至今尚未取得一致的意见。这是一种操作性的定义，它并没有对智力的内涵作出明确的规定。这一定义说明，智力属于认知能力的范畴，但它不是个体认知能力的某一组成部分，而是各种认知能力的有机结合而形成的一种综合能力。......
2025-09-30
-
高等数学上册：导数概念详细阅读
1）几个实际问题（1）平面曲线的切线问题设点M0（x0，y0）与M（x，y）分别是平面曲线y＝f（x）上的一个定点与动点，则割线MM0的斜率为根据切线的定义可知，当M→M0，即Δx→0时，若存在，则该极限就等于切线的斜率，即因此曲线y＝f（x）在点M0（x0，y0）处的切线方程为y－y0＝k（x－x0）（2）变速直线运动的瞬时速度问题设质点M沿某直线作s＝s（t）的变速直线运动，s（t）为t时刻质......
2025-09-30
-
基准的概念及工艺应用详细阅读
图4-6设计基准2.工艺基准在零件加工、测量和装配过程中所使用的基准称为工艺基准，又可分为定位基准、测量基准、工序基准和装配基准。定位基准是指零件在加工过程中，用于确定零件在机床或夹具上的位置的基准。测量基准是测量已加工表面的尺寸及各表面之间位置精度的基准，主要用于零件的检验。......
2025-09-29
- 详细阅读
-
复变函数导数及应用-复变函数及其应用详细阅读
复变函数导数的定义在形式上与一元实变函数一致.定义1 设函数w = f(z)在点z0的某个邻域内有定义,且z0+△z是该邻域中的点,如果极限存在,我们称f(z)在点z0处可导(或可微),并称此极限值为f(z)在z0 点处的导数,记作若函数w = f(z)在点z0可导,导数为f′(z0),那么对于任意给定的ε ＞0,相应地存在δ(ε)＞0,使得当0 ＜|△z|＜δ时,有若函数w =f(z)在区域D内......
2025-09-30
相关推荐