一、连续函数的概念
在自然界中有许多现象都是连续不断地变化的，如，气温随着时间的变化而连续变化；金属轴的长度随气温有极微小的改变也是连续变化的等.这些现象反映在数量关系上就是我们所说的连续性.函数的连续性反映在几何上可以看作一条不间断的曲线；下面给出连续函数的概念.
（一）函数的增量
增量的定义，简单说，就是变化后的量减去变化前的量.
例如：早晨t1=8时，温度T1=2℃，中午t2=14时，温度T2=12℃，则时间的增量为Δt=14-8=6时，温度的增量为ΔT=12-2=10℃，增量可正可负.
定义1 对y=f（x），若自变量从初值x0变为终值x时，差值Δx=x-x0称为自变量x的增量（通常称为改变量），记为Δx，相应的函数y的增量
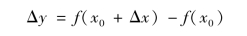
（二）函数的连续性
定义2 一设函数y=f（x）在x0的某一个邻域U（x0，δ）内有定义，当自变量x在x0点有一个增量（改变量）Δx时，相应的函数y的增量Δy=f（x0+Δx）-f（x0），当Δx趋近0时，Δy也趋近于0，即：
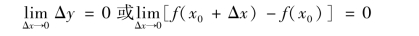
则称函数f（x）在点x0处连续.
由于Δx=x-x0，x=x0+Δx 所以，Δx→0，x→x0，所以
由此，可以得出连续的第二定义.
定义3 二设函数y=f（x）在x0的某一个邻域U（x0，δ）内有定义，若
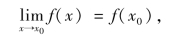
则称函数f（x）在点x0处连续.
由定义3可知，一个函数f（x）在点x0连续必须满足下列3个条件（通常称为三要素）：
（1）函数y=f（x）在x0的一个邻域有定义，即有确定的函数值；
注意：（1）函数y=f（x）在x0点有极限并不要求其在x0点有定义，而函数y=f（x）在点x=x0连续，则要求其在x0点本身和它的邻域内有定义.
（2）如果3个条件有一个不满足，则函数f（x）在x0点不连续.
或
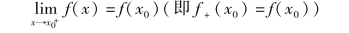
则称函数y=f（x）在点x0处左（右）连续.
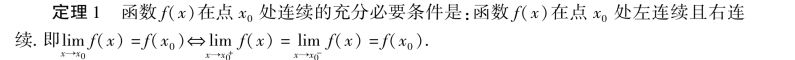
定义5 若函数f（x）在开区间（a，b）内每一点都连续，则称函数f（x）在开区间（a，b）内连续.若函数f（x）在开区间（a，b）内连续，且在点a右连续，在点b左连续，则称函数f（x）在闭区间[a，b]上连续.
若函数f（x）在它的定义域内每一点都连续，则称f（x）为连续函数.
注意：对于讨论分段函数f（x）在分段点x=a处连续性问题，如果函数f（x）在x=a左右两边的表达式相同，则直接计算函数f（x）在x=a处的极限，如例2；如果函数f（x）在x=a左右两边的表达式不相同，则要分别计算函数f（x）在x=a处的左、右极限，再确定函数f（x）在x=a处的极限，如例1、例3.
二、连续函数的运算性质
设函数f（x）与g（x）在x0处连续，则
（1）f（x）±g（x），f（x）·g（x）在x0处连续；根据函数连续的定义及函数的和差积商的极限运算法则，可给出上述定理的证明.
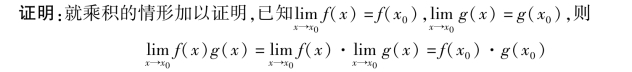
即函数f（x）g（x）在x0处连续.
其他情形请读者作为练习自行完成.
三、初等函数的连续性
定理2 若函数u=φ（x）在x0处连续，u0=φ（x0），函数y=f（u）在u0处连续，则复合函数y=f（φ（x））在x0处连续.
如u=sinx在x=1处连续，y=u2在sin1处连续，则复合函数y=（sinx）2在x=1处连续.
定理3 若函数y=f（x）在某区间上严格单调且连续，则其反函数y=f-1（x）在相应的区间上也严格单调且连续.
由以上可得出结论：基本初等函数、初等函数在其定义区间内连续.
四、间断点(www.chuimin.cn)
定义6 若函数f（x）在点x0处不连续，则称点x0是函数f（x）一个间断点或不连续点.
下面以具体的例子说明函数间断点的类型.
1.f（x）在点x0无定义.
图1.14
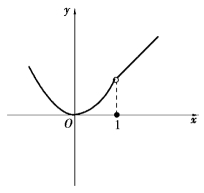
图1.15
这种类型的间断点称为跳跃间断点.
一般情况下，函数f（x）的间断点x0分为两类：若f（x）在x0的左、右极限都存在，则称x0为f（x）第一类间断点，在第一类间断点中，若f（x）在x0的左、右极限相等，则x0为可去间断点；若f（x）在x0的左、右极限不相等，则x0为跳跃间断点.不是第一类间断点的间断点，称为第二类间断点.如无穷间断点、振荡间断点.
*五、闭区间上连续函数的性质
定理4（最值性） 若函数f（x）在闭区间[a，b]上连续，则f（x）在闭区间[a，b]上可同时取得最大值与最小值.
定理5（零点定理） 若函数f（x）在闭区间[a，b]上连续，且f（a）·f（b）＜0，则在（a，b）内至少存在一点ξ，使得f（ξ）=0.
定理6（介值定理） 若函数f（x）在闭区间[a，b]上连续，且f（a）≠f（b），c为介于f（a）与f（b）的任意数，则在（a，b）内至少存在一点ξ，使得f（ξ）= C.
由定理6与定理8知，对于在闭区间[a，b]上连续函数f（x），可取得介于其在闭区间[a，b]上的最大值与最小值之间的任意一个数.
*【例题12】 证明方程x-2sinx=1至少有一个根.
证明：设f（x）=x-2sinx-1，因为f（x）为初等函数，在其定义区间（-∞，+∞）内连续，所以，f（x）在[0，3]上连续.又f（0）=-1＜0，f（3）=3-2sin3-1＞0，根据零点定理，在（0，3）内至少存在一个ξ，使得f（ξ）=0，即方程x-2sinx=1至少有一个根.
习题1.8
1.求下列函数的间断点.
复习题一
一、填空题
二、选择题
5.当x→0，ex-1是x的（ ）.
A.高阶无穷小 B.低阶无穷小 C.同阶无穷小 D.等价无穷小
三、计算题
1.分解下列复合函数.
(1)y=(1+2x)2; (2)y=sin(2x+3);
(3)y=e4x+1; (4)y=sin2(2x+1).
2.求极限.
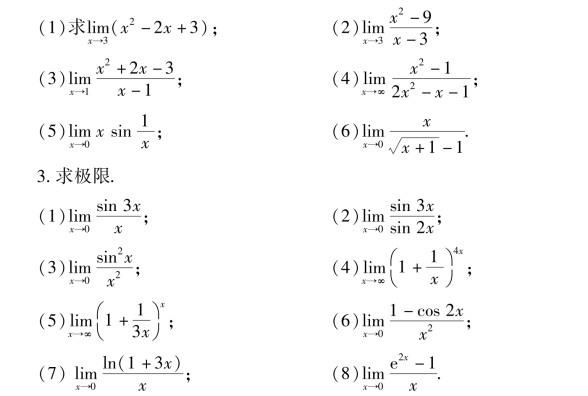
四、应用题
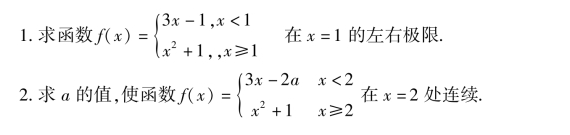
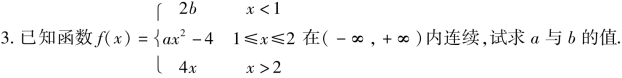
微积分发展简史（一）
有关高等数学基础的文章
，xn，yn，选项n）画y=cosx的图像，并用蓝色，点画线，五角星标注.clearclcx=0：0.02：2*piy=cosplot·画y=x^3图像，用黑色、实线、星号表示.·clear·clcx=0：0.2：5·y=x.^3·plotholdon/off命令控制是保持原有图形还是刷新原有图形，不带参数的hold命令在两种状态之间进行切换.绘制分段函数程序如下：x=-10：0.1：0y=x.^2plot(x,y)holdonx=0：0.1：10y=x.^3plot(x,y)练习一1.谈谈你对MATLAB的认识.2.绘制y=sin2x在[0，2π]范围内的图像.3.绘制y=x3cosx的图像用蓝色、实线、三角形标注（要求写出语句，......
2023-11-20
一、求积分求积分由函数int来实现.该函数的一般调用格式为：int（s）：没有指定积分变量和积分阶数时，系统按默认变量对被积函数或符号表达式s求不定积分.int（s，v）：以v为自变量，对被积函数或符号表达式s求不定积分.int（s，v，a，b）：求定积分运算.a，b分别表示定积分的下限和上限.该函数求被积函数在区间[a，b]上的定积分.a和b可以是两个具体的数，也可以是一个符号表达式，还可以是无......
2023-11-20
1）连续函数的四则运算法则函数的连续性是由函数的极限来定义的，所以根据极限的四则运算法则，可得下面的连续函数的四则运算法则.定理1若函数f（x）与g（x）都在点x0处连续，则函数f（x）±g（x），f（x）·g（x）都在点x0处连续，若再增加条件g（x0）≠0，则也在点x0处连续.证设函数f（x），g（x）都在点x0处连续，所以由极限的加、减、乘运算法则，可得即f（x）±g（x），f（x）·g......
2023-11-19
一、曲线凹凸性的定义为了较准确地描述函数的图形，仅知道函数的单调区间和极值是不行的，比如说，f（x）在[a，b]上单调，这时会出现图3.6中的几种情况，l1是一段凸弧，l2是一段凹弧，l3既有凸的部分，也有凹的部分，曲线具有这种凸和凹的性质，称为凸凹性.图3.6曲线的凸凹性从几何意义上看，凸弧具有这种特点：从中任取两点，连接此两点的弦总在曲线的下方.进而不难知道，在[a，b]中任意取两个点函数在......
2023-11-20
一、积分变上限函数设函数f（x）在区间[a，b]上连续，并且设x为[a，b]上的一点.则函数f（x）在部分区间[a，x]上的定积分∫xaf（x）dx存在且连续，为了区分积分变量，我们用t表示积分变量，记为定理1（微积分基本定理）如果函数f（x）在区间[a，b]上连续，则积分变上限函数在[a，b]上具有导数，并且它的导数为图5.8定理1表明，Φ（x）是连续函数f（x）的一个原函数，因此可得.定理2......
2023-11-20
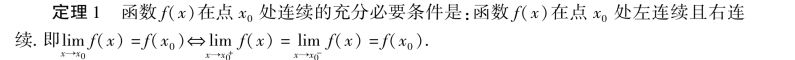
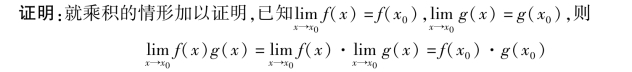
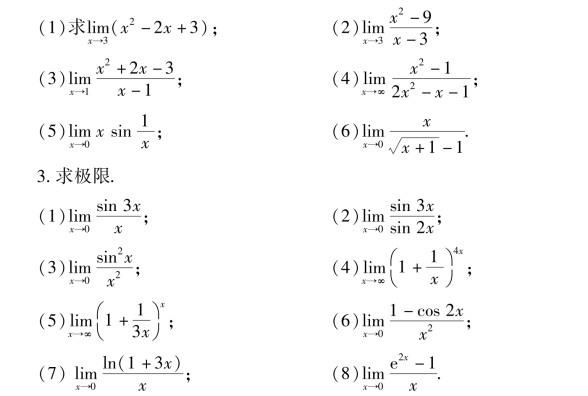
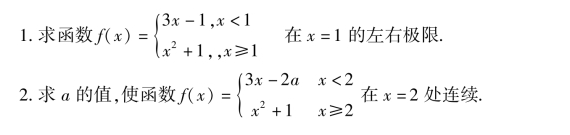
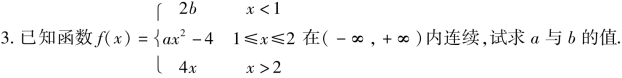
相关推荐