联合国教科文组织对文化政策的理解和界定比较宽泛但十分明确。如此看来，文化政策显然不仅关涉“文化发展”，而且隐秘地关涉社会文化的规训和控制。在这个意义上，文化政策是社会文化治理和规训体系的重要组成部分。现代性国家透过文化政策生产“权力和符号”，“教育公民成为有品位的人，品位的形成就是文化管理或文化政策”。......
2025-09-29
高等数学基础：数列极限的定义及其在微积分学中的重要性
【摘要】：极限是微积分学中一个基本概念，微分学与积分学的许多概念都是由极限引入的，并且最终由极限知识来解决.因此它在微积分学中占有非常重要的地位.我国春秋战国时期的《庄子·天下篇》中说：“一尺之棰，日取其半，万世不竭”，这就是极限的最朴素思想.一、数列极限的定义（一）数列的概念定义1按自然数顺序递增的一列数称为数列.即简记为：{un}.数列中的每一个数称为数列的项，其中第一项u1称为数列的首项，第n项称为
极限是微积分学中一个基本概念，微分学与积分学的许多概念都是由极限引入的，并且最终由极限知识来解决.因此它在微积分学中占有非常重要的地位.
我国春秋战国时期的《庄子·天下篇》中说：“一尺之棰，日取其半，万世不竭”，这就是极限的最朴素思想.
一、数列极限的定义
（一）数列的概念
定义1 按自然数顺序递增的一列数称为数列.即
简记为：{un}.数列中的每一个数称为数列的项，其中第一项u1称为数列的首项，第n项称为数列的通项或一般项.
注：①数列分为有穷数列和无穷数列，比如：1，3，5，7，9这5项数值构成一个有穷数列.对此，本书不作讨论.本书所讨论的数列都是无穷数列.
②对于数列{un}，若对任何正整数n，都有un≤un+1成立，则称数列{un}为单调递增数列；若对任何正整数n，都有un≥un+1成立，则称数列{un}为单调递减数列.
（二）数列的极限
【引例】 {un}：1，2，3，4，5，…，n…；
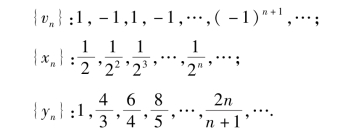
根据引例列举的几个数列来看，当n无限增大时，相应项的值的变化情况各不相同，在变化过程中：
数列{un}的一般项n趋近于无穷大的数，它没有一个确定的终极趋势；
数列{vn}的一般项un=（-1）n+1在1与-1之间交替变化，它没有一个确定的值；
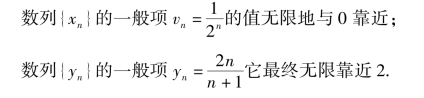
从上面几个例题可以看出，当n无限增大时，有的数列的值无限地接近一个定数，有的数列则在n无限增大的过程中飘浮不定.对于这些现象，用数学语言描述出来就有如下定义.
定义2 对于数列{un}，如果当n无限增大时，通项un无限趋近于常数A，则称A为数列{un}的极限，或称数列un收敛于A.记为
如果数列{un}没有极限（当n→∞时），称{un}发散.
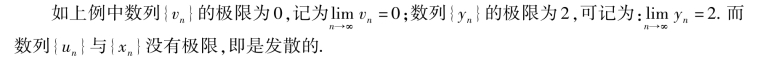
关于极限，有一点是必须明确的，极限是变量变化的终极趋势，也可以说是变量变化的最终结果.因此，可以说，数列极限的值与数列前面有限项的值无关.
【例题1】 观察以下数列的变化趋势，确定它们的敛散性，对收敛数列，写出其极限.
（3）un=（-1）n+1即1，-1，1，-1，…，（-1）n+1，…当n为奇数时，un=1，当n为偶数时，un=-1，即当n无限增大时，奇数项等于1，而偶数项等于-1，un没有一个固定的终极趋势，因此该数列发散.
二、函数的极限
（一）自变量趋于无穷时的极限
1.x→+∞时的极限
由例子可以得出自变量趋于正无穷时极限定义.
这个概念描述的是当自变量朝正无穷远方向变化时，相应的函数值趋近于某个常数的变化趋势.当然，不是所有的函数都有这种性质，比如函数f（x）=x+1，可以看到，当自变量x朝正无穷远方向变化时（即x→+∞），相应的函数值f（x）=x+1也随之无限增大，不会趋于任何常数，因此这个函数在x趋于正无穷大时没有极限.
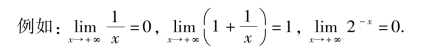
2.x→-∞时的极限
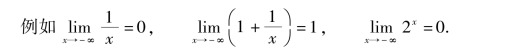
3.x→∞时的极限
(https://www.chuimin.cn)
（1）A是唯一的确定的常数；
（2）x→∞既表示趋于+∞，也表示趋于-∞.
【例题2】 讨论当x→∞，下列函数的极限是否存在.
所以当x→∞，f（x）=2的极限不存在.
（二）x→x0时自变量趋于有限值时函数的极限
在引入概念之前，我们前先看一个例子.
其实，当x无限趋近于1时，相应函数值就无限趋近2（图1.13）.这时称f（x）当x→1时以2为极限.
为此我们可以给出函数在某定点的极限的定义.
定义6 设函数f（x）在x0的某一去心邻域U°（x0，δ）内有定义，当x在U°（x0，δ）内无限趋近x0时，相应的函数值f（x）无限趋近于常数A，则称f（x）当x→x0时以A为极限，记作
值得注意的是：
②在x无限趋近x0的过程中，既可以从大于x0的方向趋近x0，也可以从小于x0的方向趋近于x0，整个过程没有任何方向限制.
【例题3】 讨论x→0时cosx的极限.
解：当x→x0，即cosx无限趋近于cosx0，
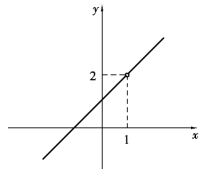
图1.13
有时我们在考察函数时只考虑在x0点左邻域（或它的右邻域内）有定义的情况，为此我们给出函数当x从x0的左侧无限接近于x0和从x0的右侧无限接近于x0时的极限定义.
定义7 右极限的定义：设函数f（x）在x0的某个右半邻域（x0，x0+δ）内有定义，当x从右边（大于x0的方向）无限接近x0时，相应的函数值f（x）无限趋近于常数A，则称函数f（x）在x0点存在右极限，记作
左极限的定义：设函数f（x）在x0的某个左半邻域（x0-δ，x0）内有定义，当x从左边（小于x0的方向）无限接近x0时，相应的函数值f（x）无限趋近于常数A，则称函数f（x）在x0点存在左极限，记作
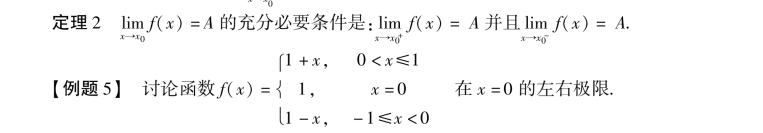
解：函数f（x）在x=0点的U°（0，1）内有定义，当x从0的右侧趋于0时，相应的函数值
习题1.4
1.观察下列数列的变化，写出它们的极限.
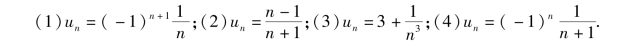
2.利用函数的图形求下列极限.
相关文章
- 详细阅读
-
记忆的概念及其在成功中的重要性详细阅读
从信息加工观点来看，记忆就是人脑对所输入的信息进行编码、贮存和提取的过程。仅上过4个月小学，后来成为美国总统的林肯也有着惊人的记忆力和渊博的知识，他的成功与记忆力突出有很大的关系。茅盾先生辉煌的成就与他出色的记忆力是分不开的。周恩来总理也常因为准确的记忆力引起人们的惊叹，使他周旋于国际政治舞台得心应手，非凡的记忆力是他取得了巨大成功的一个重要因素。......
2025-09-30
-
牛顿运动定律及其在自然科学基础中的重要性详细阅读
牛顿第一定律还指出，由于任何物体都具有惯性，要使物体的运动状态发生变化就必须有外力作用。牛顿第一定律是大量观察与实验事实的抽象与概括。这一事实使我们相信牛顿第一定律是正确的，是客观事实的概括和总结。牛顿第一定律定义了惯性系。而牛顿第一定律不成立的参照系称为非惯性系。这就是牛顿第三定律，又叫作用力和反作用力定律。牛顿第三定律实际上是关于力的性质的定律。......
2025-09-29
-
高等数学：二重极限定义及性质详细阅读
定义2 设二元函数点f（x，y）在点P0（x0，y0）的某邻域内有定义（点P0可以除外），如果该邻域内的点P（x，y）以任意方式无限趋于点P0（x0，y0）时，对应的函数值f（x，y）无限接近于一个确定的常数A，则称常数A为函数f（x，y）当（x，y）→（x0，y0）时的极限，记作为了区别于一元函数的极限，我们把二元函数的极限叫作二重极限.必须注意，所谓二重极限存在，是指点P（x，y）以任何方式趋......
2025-09-30
-
保险的含义及其在投资与理财中的重要性详细阅读
从法律意义上说，保险是一种合同行为，即通过签订保险合同，明确双方当事人的权利与义务。被保险人以缴纳保费获取保险合同规定范围内的赔偿，保险人则有收受保费的权利和提供赔偿的义务。由此可见，保险乃是经济关系与法律关系的统一。保险要素指构成保险关系的主要因素。保险要素的主要指保险人、投保人、被保险人、保险标的及可保风险。如果投保人或被保险人未指定受益人，则他的法定继承人即为受益人。......
2025-09-29
-
艺术物种：审美反应及其在进化中的重要性详细阅读
也就是说，他们犯了我在第一章中指出的科学家们普遍存在的错误：把任何基于感性的评价都视为审美的。审美反应使对象的吸引力或其他方面变得生动，从而使对象凸显出来。而这一等式由于当今人类做出的对等回应的审美特征而变得更加可信。......
2025-09-30
- 详细阅读
-
策划的重要性及其定义与作用详细阅读
赵承宗等著述的《策划学》认为：“策划又称策画。包含有策划、计划、打算之意。策划活动,在本质上是人类特有的一种自觉能动活动。——策划活动就是自觉运用脑力的一种理性行为,它是人们对自己所要进行的活动,事先在观念中做出打算,也就是预先做出计划、安排。对要达到什么目的,如何来达到目的,依靠什么来进行,具体步骤怎样等等一系列问题,进行具体的设计、计划、筹划。”......
2025-09-29
相关推荐