一、积分变上限函数设函数f（x）在区间[a，b]上连续，并且设x为[a，b]上的一点.则函数f（x）在部分区间[a，x]上的定积分∫xaf（x）dx存在且连续，为了区分积分变量，我们用t表示积分变量，记为定理1（微积分基本定理）如果函数f（x）在区间[a，b]上连续，则积分变上限函数在[a，b]上具有导数，并且它的导数为图5.8定理1表明，Φ（x）是连续函数f（x）的一个原函数，因此可得.定理2......
2023-11-20
基本初等函数-高等数学基础
【摘要】：一、基本初等函数我们常用的基本初等函数有6种，分别是常数函数、指数函数、对数函数、幂函数、三角函数及反三角函数.（一）常数函数y=c（c为常数）.（二）幂函数1.函数y=xα称为幂函数，其中x是自变量，α是常数.2.幂函数的性质及图像的变化规律①所有的幂函数在（0，+∞）都有定义，并且图像都过点（1，1）.图1.9②α＞0时，幂函数的图像通过原点和点（1，1），并且在区间[0，+∞）上是增函数.③
一、基本初等函数
我们常用的基本初等函数有6种，分别是常数函数、指数函数、对数函数、幂函数、三角函数及反三角函数.
（一）常数函数
y=c（c为常数）.
（二）幂函数
2.幂函数的性质及图像的变化规律
①所有的幂函数在（0，+∞）都有定义，并且图像都过点（1，1）.
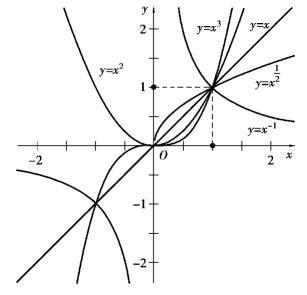
图1.9
②α＞0时，幂函数的图像通过原点和点（1，1），并且在区间[0，+∞）上是增函数.
③当α＞1时，幂函数的图像在区间[0，+∞）上下凸且快速上升；当0＜α＜1时，幂函数的图像在区间[0，+∞）上上凸且上升速度缓慢.
④α＜0时，幂函数的图像过点（1，1），在区间（0，+∞）上是下凸递减.在第一象限内，当x从右边趋向原点时，图像在y轴右方无限地逼近y轴正半轴，当x趋于+∞时，图像在x轴上方无限地逼近x轴正半轴，即以x，y轴为渐近线.
（三）指数函数
1.指数运算公式
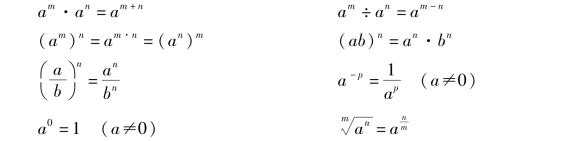
2.指数函数y=ax在底数a＞1及0＜a＜1这两种情况下的图像和性质
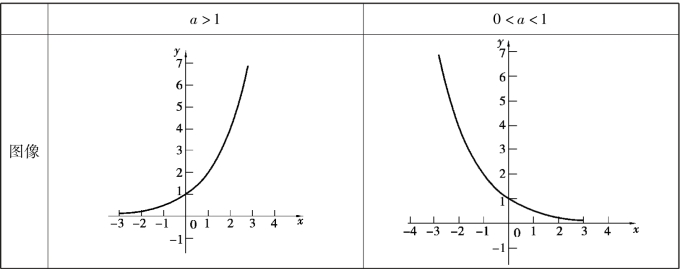
续表
（四）对数函数
1.对数运算公式
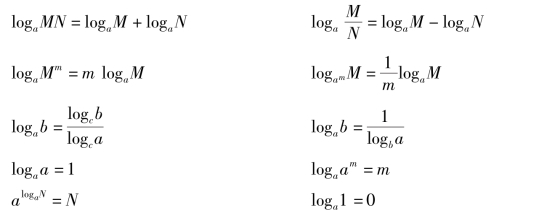
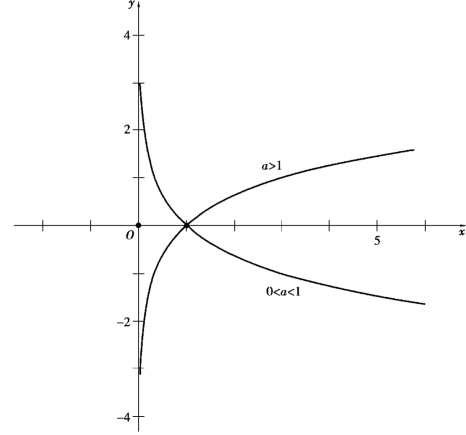
图1.10
2.对数函数图像与特征
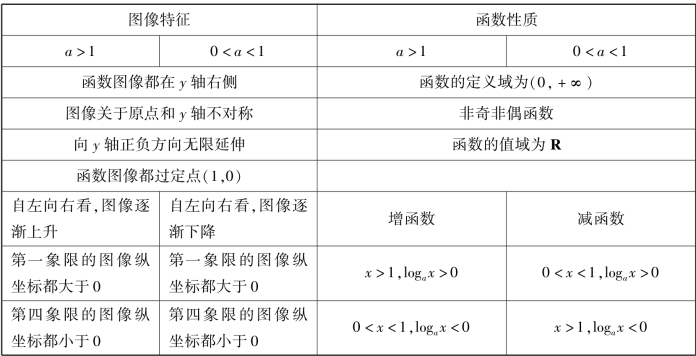
特殊的当底数a=e（e=2.718…）时，y=lnx（x＞0）称为自然对数.
自然对数的一些公式：ln1=0，lne=1，elnx=x，lnxa=alnx.
（五）三角函数
三角函数包含正弦函数（y=sinx）、余弦函数（y=cosx）、正切函数（y=tanx），余切函数（y=cotx），正割函数（y=secx），余割函数（y=cscx）.
1.三角函数公式
（1）商的公式：
（2）平方公式：
sin2x+cos2x=1;
1+tan2x=sec2x;
1+cot2x=csc2x.
（3）二倍角公式：
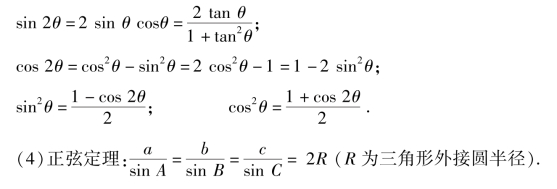
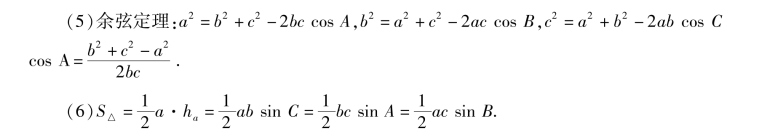
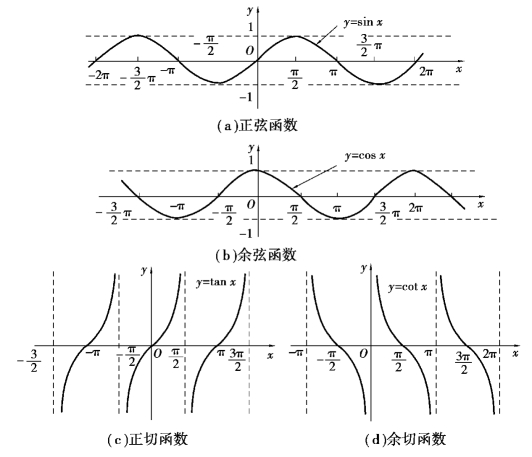
2.正弦函数、余弦函数、正切函数和余切函数的图像
图1.11所示为正弦函数、余弦函数、正切函数和余切函数的图像.
(www.chuimin.cn)
图1.11
（六）反三角函数
反三角函数包含反正弦函数（y=arcsinx），反余弦函数（y=arccosx），反正切函数（y=arctanx），反余切函数（y=arccotx）.
二、复合函数
（一）定义
若y是u的函数：y=f（u），而u又是x的函数：u=φ（x），且φ（x）的函数值的全部或部分在f（u）的定义域内，那么，y通过u的联系也是x的函数，我们称y=f[φ（x）]是由函数y=f（u）及u=φ（x）复合而成的函数，简称复合函数，其中u称为中间变量.
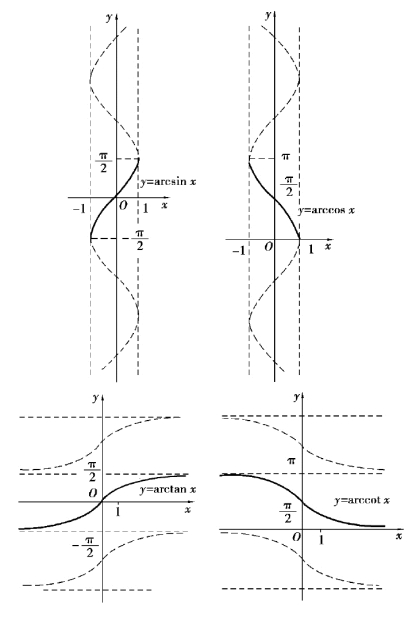
图1.12 反三角函数图像
【例题1】 设y=f（u）=3u，u=φ（x）=tanx，求复合函数y=f[φ（x）].
解：y=f[φ（x）]=f（u）=f（tanx）=3tanx.
【例题2】 求y=2u2+1与u=cosx构成的复合函数.
解：将u=cosx代入y=2u2+1中，即为所求的复合函数
y=2cos2x+1，定义域为（-∞，+∞）.
（二）复合函数的分解
复合函数的分解是指把一个复合函数分解成基本初等函数或基本初等函数的四则运算.
【例题4】 分解下列复合函数.
(1)y=cosx2
(2)y=sin22x
解：
（1）所给函数可分解为
（2）所给函数可分解为
（3）所给函数可分解为
（4）所给函数可分解为
注：并不是任意两个函数就能复合；复合函数还可以由更多函数构成.
例如：函数y=arcsinu与函数u=2+x2是不能复合成一个函数的.
因为对于u=2+x2的定义域（-∞，+∞）中的任何x值所对应的u值（都大于或等于2），使y=arcsinu都没有定义.
注：复合函数的分解是求复合函数导数的基础，一定要掌握好.
三、初等函数
基本初等函数经过有限次的四则运算及有限次的函数复合所产生并且能用一个解析式表出的函数称为初等函数.因此初等函数包括（1）基本初等函数；（2）基本初等函数经过有限次复合而成的函数；（3）复合函数.而分段函数不一定是初等函数.
习题1.3
1.指出下列函数的复合函数.
(1)y=u2,u=2x-1; (2)y=u3,u=cosx;
2.分解下列复合函数.
(1)y=(3x-1)5; (2)y=sin(2x+1);
(3)y=e4x-1; (4)y=sin2(2x+3);
有关高等数学基础的文章
- 详细阅读
-
初等函数及其反函数-高等数学 上册详细阅读
1）反函数设函数y＝f（x）的定义域为D，值域为f（D），在函数y＝f（x）中，x为自变量，y为因变量，x可以独立取值，而y却按确定的法则随x而定，即函数y＝f（x）反映的是y怎样随x而定的法则；反过来，对于y∈f（D），若D内总有确定的x与之对应，使得f（x）＝y成立，这样得到一个以y为自变量，x为因变量的函数，称该函数为y＝f（x）的反函数，记作x＝f－1（y），其定义域为f（D），值域为D.......
2023-11-19
-
MATLAB简介|高等数学基础详细阅读
，xn，yn，选项n）画y=cosx的图像，并用蓝色，点画线，五角星标注.clearclcx=0：0.02：2*piy=cosplot·画y=x^3图像，用黑色、实线、星号表示.·clear·clcx=0：0.2：5·y=x.^3·plotholdon/off命令控制是保持原有图形还是刷新原有图形，不带参数的hold命令在两种状态之间进行切换.绘制分段函数程序如下：x=-10：0.1：0y=x.^2plot(x,y)holdonx=0：0.1：10y=x.^3plot(x,y)练习一1.谈谈你对MATLAB的认识.2.绘制y=sin2x在[0，2π]范围内的图像.3.绘制y=x3cosx的图像用蓝色、实线、三角形标注（要求写出语句，......
2023-11-20
-
《高等数学基础》MATLAB：积分求解详细阅读
一、求积分求积分由函数int来实现.该函数的一般调用格式为：int（s）：没有指定积分变量和积分阶数时，系统按默认变量对被积函数或符号表达式s求不定积分.int（s，v）：以v为自变量，对被积函数或符号表达式s求不定积分.int（s，v，a，b）：求定积分运算.a，b分别表示定积分的下限和上限.该函数求被积函数在区间[a，b]上的定积分.a和b可以是两个具体的数，也可以是一个符号表达式，还可以是无......
2023-11-20
-
高等数学：函数基本性态详细阅读
初等数学中已经简单介绍了函数的有界性、单调性、奇偶性、周期性，下面分别对它们作简要概括.1）有界性定义3设函数f（x）在区间I上有定义，若存在数M1，使得当x∈I时，恒有f（x）≤M1则称函数f（x）在数集I上有上界，M1为f（x）在I上的一个上界；若存在数M2，使得当x∈I时，恒有f（x）≥M2则称函数f（x）在数集I上有下界，M2为f（x）在I上的一个下界；若f（x）在数集I上既有上界，又有......
2023-11-19
- 详细阅读
-
高等数学基础：曲线凹凸和拐点详细阅读
一、曲线凹凸性的定义为了较准确地描述函数的图形，仅知道函数的单调区间和极值是不行的，比如说，f（x）在[a，b]上单调，这时会出现图3.6中的几种情况，l1是一段凸弧，l2是一段凹弧，l3既有凸的部分，也有凹的部分，曲线具有这种凸和凹的性质，称为凸凹性.图3.6曲线的凸凹性从几何意义上看，凸弧具有这种特点：从中任取两点，连接此两点的弦总在曲线的下方.进而不难知道，在[a，b]中任意取两个点函数在......
2023-11-20
- 详细阅读
相关推荐