中国现代数学先驱——熊庆来......
2023-11-20
高等数学基础：函数性质概述
【摘要】：一、函数的有界性如果对属于某一区间I的所有x值总有│f（x）│≤M成立，其中M是一个与x无关的常数，那么我们就称f（x）在区间I有界，否则便称无界.注：一个函数，如果在其整个定义域内有界，则称为有界函数.例如：函数y=cosx在（-∞，+∞）内是有界的.再如：当x∈（-∞，+∞）时，恒有|sinx|≤1，所以函数f（x）=sinx在（-∞，+∞）内是有界函数.这里M=1（当然，也可以取大于1的任何
一、函数的有界性
如果对属于某一区间I的所有x值总有│f（x）│≤M成立，其中M是一个与x无关的常数，那么我们就称f（x）在区间I有界，否则便称无界.
注：一个函数，如果在其整个定义域内有界，则称为有界函数.
例如：函数y=cosx在（-∞，+∞）内是有界的.
再如：当x∈（-∞，+∞）时，恒有|sinx|≤1，所以函数f（x）=sinx在（-∞，+∞）内是有界函数.这里M=1（当然，也可以取大于1的任何数作为M而使|f（x）|＜M成立）.
二、函数的单调性
如果函数f（x）在区间（a，b）内随着x的增大而增大，即对于（a，b）内任意两点x1及x2，当x1＜x2时，有f（x1）＜f（x2），则称函数f（x）在区间（a，b）内是单调增加的，称（a，b）为单增区间.如果函数f（x）在区间（a，b）内随着x增大而减小，即对于（a，b）内任意两点x1及x2，当x1＜x2时，有f（x1）＞f（x2），则称函数f（x）在区间（a，b）内是单调减小的，称（a，b）为单减区间.
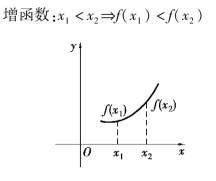
图1.6
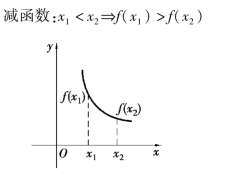
图1.7
再如：函数f（x）=x2在区间（-∞，0）上是单调减小的，在区间（0，+∞）上是单调增加的.
三、函数的奇偶性
如果函数f（x）对于定义域（-a，a）内的任意x都满足f（-x）=f（x），则f（x）称为偶函数；如果函数f（x）对于定义域内的任意x都满足f（-x）=-f（x），则f（x）称为奇函数.
注：偶函数的图形是关于y轴对称的，如函数y=cosx；奇函数的图形是关于原点对称的，如y=sinx.
【例题1】 判断下列函数的奇偶性.
(1)f(x)=x5-2x3(2)f(x)=cos3x
解：（1）f（-x）=（-x）5-2（-x）3=-x5+2x3=-（x5-2x3）=-f（x）
由函数奇偶性的定义可知，该函数在其定义区间内为偶函数.
(2)f(-x)=cos(-3x)=cos3x=f(x)
由函数奇偶性的定义可知，该函数在其定义区间内为偶函数.
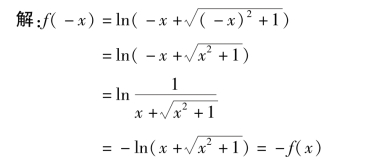
由函数奇偶性的定义可知，该函数在其定义区间内为奇函数.
四、函数的周期性
对于函数f（x），若存在一个不为零的数l，使得关系式f（x+l）=f（x）对于定义域内任何x值都成立，则f（x）称为周期函数，l是f（x）的周期.
注：通常所说的周期函数的周期是指最小正周期，并非每一个函数都有最小正周期，如常数函数y=a及狄利克雷函数.
一般函数sinx，cosx是以2π为周期的周期函数；函数tanx是以π为周期的周期函数.(www.chuimin.cn)
如果某个函数可以分解成两个函数f1（x）与f2（x），设f1（x）与f2（x）分别以T1与T2为周期，并且，如果存在T1，T2的（正整数倍的）最小公倍数T，则函数f1（x）+f2（x）以T为周期.
【例题3】 求下列函数的周期：
五、反函数
（一）反函数的定义
定义 设y=f（x）为定义在D上的函数，其值域为M.若对于数集M中的每个数y，数集D中都有唯一的一个数x使f（x）=y，这就是说变量x是变量y的函数.这个函数称为函数y=f（x）的反函数，记为x=f-1（y）.其定义域为M，值域为 D.
习惯上，常用x表示自变量，y表示因变量，因此函数y=f（x）的反函数x=f-1（y）常改写为y=f-1（x），函数y=f（x）称为原函数；函数y=f（x）与其反函数y=f-1（x）之间存在着如下关系：
f-1(f(x))=x, f(f-1(x))=x
（二）反函数的性质
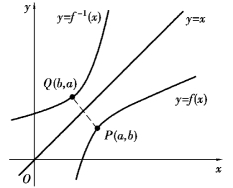
图1.8
在同一坐标平面内，y=f（x）与反函数y=f-1（x）的图形是关于直线y=x对称的，如图1.8所示.
【例题4】 求下列函数的反函数及其定义域：
（1）y=ax+b （a，b是常数，a≠0）；
(2)y=x2-1 (x＞0).
解：（1）由y=ax+b，移项解出x便得反函数：
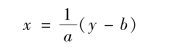
习题1.2
1.求下列函数的周期.
2.判断下列函数的奇偶性.
(1)f(x)=x4-2x2; (2)f(x)=tan5x;
3.求下列函数的反函数.
(1)y=2x+4;
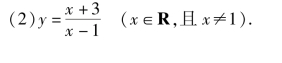
有关高等数学基础的文章
- 详细阅读
-
函数的极值和最值-高等数学基础详细阅读
解：要使材料最省，就是要罐头筒的总表面积最小.设罐头的底半径为r，高为h，如图3.5所示，则它的侧面积为2πrh，底面积为πr2，因此总表面积为图3.5于是得出结论：当所做罐头筒的高和底直径相等时，所用材料最省.习题3.21.求函数的单调区间和极值.f=x2-2x+4;f=x2-6x;y=2x3-3x2;y=x-ln(1+x);f=x3-12x.2.运用极值的第二定理求极值.f=x2-2x;f=x4-2x2.3.求函数的最值.f=x2-2x+1,x∈[-1,2];f=x2-2x,x∈[0,2];f=x3-3x,x∈[0,2];f=x4-2x2,x∈[0,2].4.已知x+y=s，运用极值第二定理证明......
2023-11-20
-
多元函数的极值分析-高等数学基础详细阅读
5.曲线L：xy=1（x＞0）上求一点，使函数f（x，y）=x2+2y2达到最小值.复习题八一、填空题二、选择题4.设z=xy，则dz=（）.A.dx+dyB.-dx-dyC.xdx+ydyD.yd......
2023-11-20
-
高等数学基础：中值定理和函数单调性详细阅读
一、拉格朗日（Lagrange）中值定理定理1（拉格朗日中值定理）若函数f（x）满足条件：（1）在闭区间[a，b]上连续；（2）在开区间（a，b）内可导；则至少存在一点ξ∈（a，b），使得或图3.1拉格朗日中值定理的几何意义：如果在闭区间[a，b]上连续的一条曲线弧y=f（x）除端点外处处具有不垂直于x轴的切线，则曲线上至少存在一点C，使得曲线在点C处的切线平行于连接曲线两端点的弦AB.显然，......
2023-11-20
-
基本初等函数-高等数学基础详细阅读
一、基本初等函数我们常用的基本初等函数有6种，分别是常数函数、指数函数、对数函数、幂函数、三角函数及反三角函数.（一）常数函数y=c（c为常数）.（二）幂函数1.函数y=xα称为幂函数，其中x是自变量，α是常数.2.幂函数的性质及图像的变化规律①所有的幂函数在（0，+∞）都有定义，并且图像都过点（1，1）.图1.9②α＞0时，幂函数的图像通过原点和点（1，1），并且在区间[0，+∞）上是增函数.③......
2023-11-20
-
高等数学基础：隐函数求导公式详细阅读
【知识点回顾】一般而言，如果x与y的函数关系隐含在方程F（x，y）=0中，即x在某一区间取值时，相应地有确定的y值和其唯一对应，则称方程F（x，y）=0所确定的函数为隐函数.隐函数求导步骤：（1）方程两边对x进行求导；（2）在求导过程中把y看成x的函数y=f（x），用复合函数求导法则进行.一、二元函数的情形在第二章第六节中已经提出了隐函数的概念，并且指出了不经过显化直接由方程求它所确定的隐函数的方......
2023-11-20
-
高等数学基础：多元函数的全微分详细阅读
【知识点回顾】y=f（x）的微分定义：由函数的增量Δy=f（x0+Δx）-f（x0）=f′（x0）Δx+o（Δx）我们把增量的近似值称为函数f（x）在点x0处的微分，即我们已经学习了一元函数的微分的概念，现在我们用类似的思想方法来学习多元函数的全增量，从而把微分的概念推广到多元函数.这里以二元函数为例.全微分的定义：设二元函数z=f（x，y）在点（x0，y0）的一个邻域内有定义，则在点（x0，y0......
2023-11-20
- 详细阅读
相关推荐