首页理论教育基本方程与分界面衔接条件

基本方程与分界面衔接条件

2025-09-30 理论教育版权反馈

【摘要】：静电场是有源无旋场，静止电荷是静电场的源，静电场的基本方程的微分形式为如图2-8-1所示，静电场的基本方程的积分形式为只要是静电场，就必须满足静电场方程。③折射定理当交界面上σ=0时，根据静电场基本方程的微分形式和辅助方程，有由此得到电位的基本方程，即为静电场的泊松方程。在不同的电介质分界处，电位应该满足一定的分界面衔接条件。

静电场是有源无旋场，静止电荷是静电场的源，静电场的基本方程的微分形式为

pagenumber_ebook=55,pagenumber_book=48

如图2-8-1所示，静电场的基本方程的积分形式为

pagenumber_ebook=55,pagenumber_book=48

只要是静电场，就必须满足静电场方程。

由此得到静电场基本方程的构成方程为D=εE。

如果介质沿着同一点出发的不同方向显示相同的性质，它就叫作各项同性介质，如砂岩。

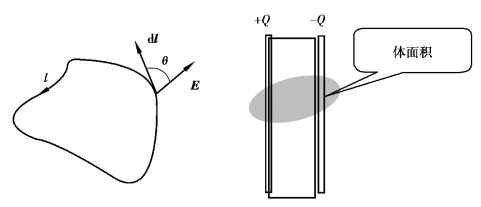
pagenumber_ebook=56,pagenumber_book=49

图2-8-1　静电场的基本方程图解

不同电介质连接，存在分界面，分界面上场矢量不连续，这不会影响积分方程的应用，却会影响微分方程，因此要研究新的微分方程来描述分界面。

如图2-8-2所示，分界面上的衔接条件为

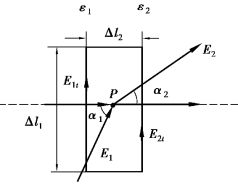
pagenumber_ebook=56,pagenumber_book=49

图2-8-2　介质分界面

①D的衔接条件为包围点P作高斯面（Δl→0）。根据∮SD·dS=q，则有-D1nΔS+D2nΔS=σΔS。当D2n-D1n=σ时，D的法向分量不连续；当σ=0时，D2n=D1n，D的法向分量连续。(https://www.chuimin.cn)

②E的衔接条件为围绕点P作一矩形回路（Δl2→0）。根据∮lE·dl=0，当Δl尽量小，则有E1tΔl-E2tΔl=0。E2t=E1t则E的切向分量连续。

③折射定理

当交界面上σ=0时，

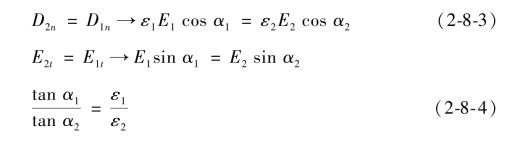
pagenumber_ebook=56,pagenumber_book=49

根据静电场基本方程的微分形式和辅助方程，有

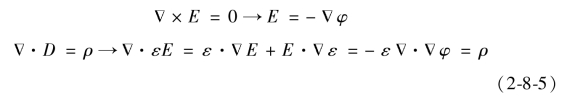
pagenumber_ebook=57,pagenumber_book=50

由此得到电位的基本方程，即

为静电场的泊松方程。当场域中没有电荷分布时，当ρ=0时式（2-8-6）变为

称为静电场的拉普拉斯方程，其中算子称为拉普拉斯算子，在直角坐标系中

pagenumber_ebook=57,pagenumber_book=50

电位的泊松方程或拉普拉斯方程是从场矢量表示的静电场的基本方程和辅助方程推导出来的。在不同的电介质分界处，电位应该满足一定的分界面衔接条件。