首页理论教育工程电磁场中的高斯通量定理应用

工程电磁场中的高斯通量定理应用

2023-11-19 理论教育版权反馈

【摘要】：高斯用数学公式表达上述结论：静电场中通过一个任意闭合曲面的电通量值等于该曲面所包围的所有电荷电量的代数和∑Ιqi除以ε0，与闭曲面外的电荷无关，称为高斯通量定理。b.穿过该高斯面的电通量容易计算。c.计算电通量和高斯面内所包围的电荷的代数和，最后由高斯定理求出场强。图2-3-3高斯面内的点电荷系图2-3-4对程序分析示意图以图2-3-4为例，应用高斯通量定理求解球形面场强的计算过程如下：

1837年，伦敦皇家学会的主任迈克尔·法拉第开始对静电场和各种绝缘材料在电场中的作用效果产生浓厚的兴趣。他制作了一对同心金属球壳构成的实验设备，两个金属球壳之间填充绝缘材料，内部球体将获得已知的正电荷。实验发现外球壳上的总电荷量与内球壳面上的总电荷量大小相同，且与两个球体之间的电介材料无关。由此推断出在两个球壳之间存在某种与介质无关的“位移”，称这个位移为通量、位移通量或简单取名为电通量。

实验还表明，当更多的正电荷在球的内部时，相应会让外球壳产生较多的负电荷，因此认为电通量和内部电荷的数量有一定的比例关系。其中的比例常数取决于所涉及的单位系统，本书使用SI单位，因此常数统一。电通量表示为Ψ（psi），内球上的总电荷为Q，由法拉第实验可得以下结论：

其中电通量计量单位为库仑。

高斯用数学公式表达上述结论：静电场中通过一个任意闭合曲面的电通量值等于该曲面所包围的所有电荷电量的代数和∑Ιqi除以ε0，与闭曲面外的电荷无关，称为高斯通量定理。可以得到积分表达式如下：

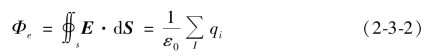
pagenumber_ebook=47,pagenumber_book=40

任一点上电场强度的散度等于体电荷密度与真空介电常数之比为

pagenumber_ebook=47,pagenumber_book=40

由电场线的连续性可知，穿过S的电场线都穿过同心球面S′，故两者的电通量相等，均为。

根据高斯通量定理可以发现：

①如图2-3-1所示，包围点电荷的同心球面S的电通量都等于；

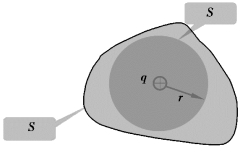
pagenumber_ebook=47,pagenumber_book=40

图2-3-1　包围点电荷的同心球面

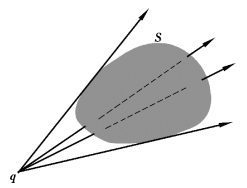
pagenumber_ebook=47,pagenumber_book=40

图2-3-2　不包围点电荷的球面

②包围点电荷的任意闭合曲面S的电通量都等于；(www.chuimin.cn)

③如图2-3-2所示，不包围点电荷q的任意闭合曲面S的电通量恒为零；

④如图2-3-3所示，点电荷系的电通量等于在高斯面内的点电荷单独存在时电通量的代数和。

应用高斯通量定理求解场强的步骤如下：

①进行对称性分析，判断能否用高斯定理来求电场强度的分布。球对称分布如图2-3-4（a）所示，包括均匀带电的球面，球体和多层同心球壳等。轴对称分布如图2-3-4（b）所示，包括无限长均匀带电的直线，圆柱面、圆柱壳等。无限大平面电荷如图2-3-4（c）所示，包括无限大的均匀带电平面，平板等。

②根据场强分布的特点，作适当的高斯面，要求：

a.待求场强的场点应在此高斯面上。

b.穿过该高斯面的电通量容易计算。一般地，高斯面各面元的法线矢量n与E平行或垂直，n与E平行时，E的大小要求处处相等，使得E能提到积分号外面。

c.计算电通量和高斯面内所包围的电荷的代数和，最后由高斯定理求出场强。

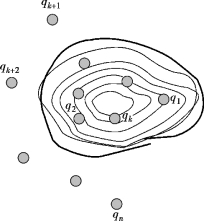
pagenumber_ebook=48,pagenumber_book=41

图2-3-3　高斯面内的点电荷系

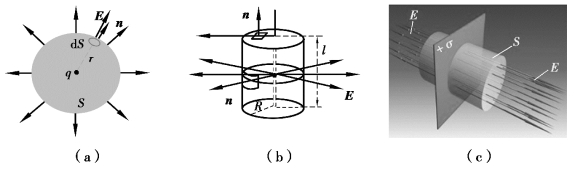
pagenumber_ebook=48,pagenumber_book=41

图2-3-4　对程序分析示意图

以图2-3-4（a）为例，应用高斯通量定理求解球形面场强的计算过程如下：

pagenumber_ebook=48,pagenumber_book=41