在发达国家，调查是通过电话进行的。菲律宾以67%的比例居于榜首，而非洲的毛里塔尼亚排名最低，比例刚刚超过5%。研究人员还发现，生活在腐败、贫穷、饥饿或暴力水平高的国家的人，诸如毛里塔尼亚，通常不认为他们的日子很难过。当涉及总体幸福感时，调查显示，最幸福的人不是没有压力的人。高压既伴有痛苦，也带来幸福。重要的是，幸福生活不是没有压力，没压力的生活也无法保证幸福。研究表明，有意义的人生，也是有压力的人生。......
2024-01-19
库仑定律解释：力与电量成正比，与距离平方成反比
【摘要】：SI给出已知的最小正（或负）电荷量为1.602×1019C，因此一库仑的负电荷大约有6×1018个电子。图2-1-3库仑定律示意图要将力写成矢量的形式，需要其他的量。库仑定律定义为真空中，两个静止点电荷之间的作用力与它们的电量的乘积成正比，与它们之间距离的平方成反比。因为库仑定律所表示的力是两者的相互作用力，因此两个电荷所受到的力大小相同方向相反。
库仑认为，在真空中，点电荷1对点电荷2的作用力，其大小正比于点电荷1的电荷量Q1与点电荷2的电荷量Q2的乘积，反比于点电荷1与点电荷2之间的距离。
其中Q1和Q2为正电荷量或负电荷量，R为q1和q2之间的距离，k为比例常数。若使用国际单位制（SI），那么Q的单位为库仑（C），R以米（m）为单位，力的单位应为牛（N）。比例常数k可写作
新常数ε0称为自由空间的介电常数，单位为法拉每米（F/m）。
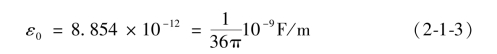
库仑对于一般的电荷是个极大的电荷单位。SI给出已知的最小正（或负）电荷量为1.602×1019C，因此一库仑的负电荷大约有6×1018个电子。库仑定律表明两个相距一米且电荷量为一库仑的电荷产生的库仑力为9×109N，电子具有9.109×10-31kg的静止质量且具有数量级为3.8×10-15m的半径。但这并不意味着电子在形状上是球形的，仅描述了缓慢移动的电子最有可能移动的区域尺寸的最大值。所有其他已知的带电粒子，包括质子，都具有较大的质量和较大的半径，并且占据体积大于电子所占据的体积。
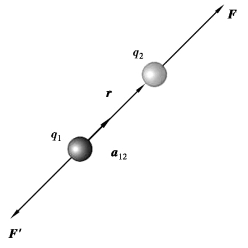
图2-1-3 库仑定律示意图
要将力写成矢量的形式，需要其他的量。库仑力是沿两个电荷的连线方向，如果电荷所带极性相同，库仑力是相斥的，如果电荷所带极性相异，库仑力是相吸的。令矢量r1位置上的电荷为q1，矢量r2位置上的电荷为q2。矢量R12=r2-r1表示从q1到q2的有向线段，如图2-1-3所示，矢量F是q1和q2具有相同极性情况下q2上所受到的力。库仑定律定义为真空中，两个静止点电荷之间的作用力与它们的电量的乘积成正比，与它们之间距离的平方成反比。因此库仑定律的矢量形式是
其中a12是在R12方向上的单位矢量。
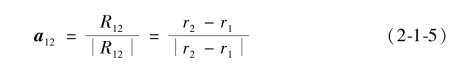
因为库仑定律所表示的力是两者的相互作用力，因此两个电荷所受到的力大小相同方向相反。由此可知
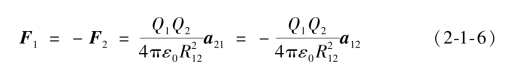
库仑定律是线性的，因此如果Q1乘以常数n，则Q2受到的库仑力也要乘以相同的常数n。电荷受到其他多个电荷作用的库仑力是这个电荷与其他电荷单独作用产生的库仑力的矢量和。
将电荷Q1固定在一个位置上，并缓慢移动另一个电荷。实验表明，第二个电荷受到了一个无处不在的力的作用，或者说第二个电荷受到了与第一个电荷相关的力场的作用。第二个电荷称为试验电荷Qt。
Ft为每单位电荷所受到的库仑力，由此可知Q1产生的点电荷的电场强度为：
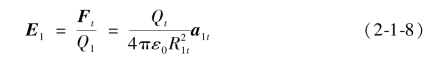
E1为单位正电荷受到电荷Q1产生的作用力，电场强度的一般表达式写为：
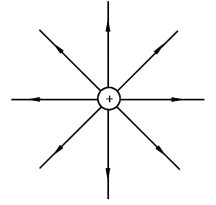
其中E是矢量函数，表示单位正电荷受到其他电荷作用下的电场，也意味着测量或计算电场时不包含试验电荷产生的电场。单位正电荷的电场分布如图2-1-4所示。
(www.chuimin.cn)
图2-1-4 单位正电荷电场分布
E的单位是牛顿每库仑。
为了避免混淆省略式（2-1-6）中大多数的下标。单点电荷的电场强度公式变为：
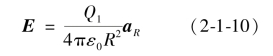
R是矢量值，是从点电荷Q到求解位置E的有向线段，aR是R方向的单位矢量。若Q1为球面坐标系的圆心，那么单位向量aR则转化为球坐标的单位矢量ar，公式中的R转化为r，因此表达式将改写为：
该场具有单个径向分量，并与r成平方反比关系。
若电荷不在坐标系原点则场不再具有球形对称性，使用矩形坐标来分析此类问题。
如点电场的场源Q的位置矢量为r′=x′ax+y′ay+z′az，如图2-1-5所示，场中一定点的位置矢量为r=xax+yay+zaz，两点位置之差r-r′用R表示，因此
位置矢量的矢量函数定义为矢量场，所以E改写为E（r）即用函数符号强调矢量函数。
因为库仑力是线性的，若场源为位于原点r1的电荷Q1和位于原点r2的电荷Q2，在P点的电场强度是单个电荷对P点作用的总和。其表达式为：
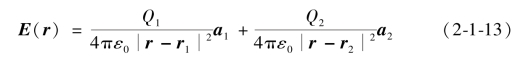
其中a1和a2分别是（r-r1）和（r-r2）方向上的单位矢量，向量r、r1、r2、r-r1、r-r2、a1和a2如图2-1-5所示。
如果在坐标系中加入更多的场源，那么某定点的电场强度为：
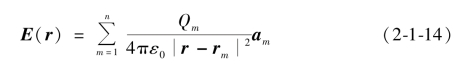
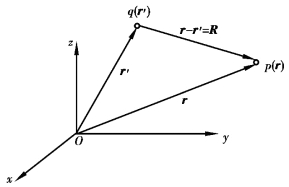
图2-1-5 点电荷的电场
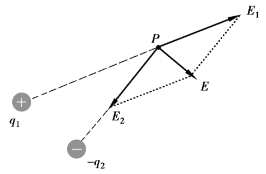
图2-1-6 矢量叠加原理
根据矢量叠加原理，如图2-1-6所示n个点电荷产生的电场强度为
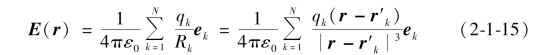
有关工程电磁场基本原理的文章
- 详细阅读
-
拼搏奋斗：付出与回报成正比!详细阅读
每当夏天来临的时候，寒号鸟全身长满了绚丽的羽毛，样子十分美丽。只有寒号鸟，既没有飞到南方去的本领，又不愿辛勤劳动，仍然整日东游西荡的，还在一个劲地炫耀自己身上漂亮的羽毛，满不在乎地跳着唱着。可是天亮之后，温暖的阳光一照，寒号鸟又忘记了夜晚的寒冷，它又会自我安慰地唱着：“得过且过！得过且过！太阳下面暖和！太阳下面暖和！”成长悟语几分耕耘，就有几分收获。......
2023-08-26
-
STM图像：概念与解释详细阅读
STM通常被认为是测量表面原子结构的工具，具有直接测量原子间距的分辨率。在解释STM图像时应注意以下几个问题。STM图像并不直接反映表面原子核的位置，STM反映的是样品波函数的起伏，在不同的偏压下，探测到的是不同的表面波函数。STM成像的倒易原理。这就可以很好地解释金属表面的STM图像会出现大的起伏的现象。......
2023-06-20
-
人生选择学：距离与尺度选项详细阅读
有的干部苦恼距离的选择难在思想观念的不一致。人与人之间距离的选择难就难在人是一个活体，是互动的。不仅包含对人际间距离的把握，还包括对物的消费量度和对事的了解度和管控度的把握。......
2024-08-19
-
力命：孟子的立命与力命策略详细阅读
孟子主张立命、俟命，要求人们要耐心等待；同时又主张力命，要求人们积极行动，以奋发有为的精神、以自强不息的姿态、以明智聪慧的选择开辟自己的未来。力命还有另一层含义，即改变自己的命。他的实力不如商纣王，对方军队在人数上占绝对优势，但离心离德，士兵临阵倒戈，转过身为周武王开路。商纣王见大势已去，自焚身亡。......
2023-10-22
-
法律命题与法律真理：抽象意图与类推解释详细阅读
在刑法没有禁止类推适用时，刑事司法实践中有许多这样的案例。比如，在马晓东侵占他人财产类推案中[98]，法官从侵占与盗窃都会给他人财产造成损失这一相似性出发，将其按照盗窃罪定罪判刑。有法官认为，同时娶二女与先后娶二女在性质与危害性上并无不同，因此此案应按重婚处理。因此，本书将情况下的弱类推统一称为类推解释。强类推与弱类推之间的区别......
2023-08-07
-
冷战联盟：不同结局及其解释与不足详细阅读
在冷战时期，欧洲大陆的两端出现了以北约为代表的西方阵营与以华约为代表的东方阵营。为什么冷战时期的北约同盟最终发展出了安全共同体，而华约同盟没有。虽然安全共同体理论意识到了联盟的动态演进性，并且认识到了和解的重要作用，[21]但在本研究问题中，此类理论可为北约的案例提供一定的解释，却无法解释华约的案例。......
2023-08-16
-
认知目标与试题外在显性距离的关系详细阅读
前面阐述了认知目标和试题之间准确对应的重要意义，但这种对应应当是“有弹性的对应”，如表5-2所示，一个认知目标可能涵盖多种任务途径。然而正如本节开头所指出的，目前我国大规模测试中，能力目标与试题之间的对应存在过于简单化，甚至有些僵化的现象。试题题干的表达与认知目标的表述保持适度距离，会是怎样的效果？我们看到的是一系列指向文本本身的具体问题，认知目标隐藏于问题引发的阅读过程和行为中。......
2023-08-17
相关推荐