1754年，英国成立了“皇家古代高尔夫球俱乐部”，大大推动了苏格兰高尔夫球运动的再次发展。1919年，“皇家古代高尔夫球俱乐部”已包办了所有英国和英联邦国家的男子高尔夫比赛，高尔夫球也开始成为一项有组织的体育运动项目。因此世界上不存在完全相同的高尔夫球场。一个标准的高尔夫球场长6 000～7 000米，宽度不限，设18个球洞。自20世纪以来，越来越多的球场已开始将会馆区作为高尔夫球俱乐部的中心。......
2023-11-03
球坐标系的基本原理及特点
【摘要】：半径r与z轴所夹的夹角为θ，当θ为常数时，在球形坐标系构成了两个面，一个是锥面，一个是球面。通过图1-2-2可知球坐标系中一点是由三个面两两垂直产生的。第三个单位矢量eφ与在圆柱坐标中eφ相同都是垂直于φ=常数的平面且与锥体和球体相切，方向指向东。如图1-2-2所示，三个单位矢量相互垂直且通过er×eθ=eφ来定义右手坐标系。
在直角坐标系下建立球形坐标系（图1-2-2（c））。首先定义原点到任意一定点的距离为r，r表示以原点为圆心，以r为半径的球面半径。半径r与z轴所夹的夹角为θ，当θ为常数时，在球形坐标系构成了两个面，一个是锥面，一个是球面。两个面交界处所对应的法线相互垂直。交界处组成的圆的半径是rsinθ，坐标值θ在经纬系统中可看作纬度，数值从正北方算起。
第三个坐标值φ与圆柱坐标系定义的角度φ完全相同，角φ是半径r在xy所在平面的投影与x轴的夹角。此角度对应的是经度，夹角越往东，角的度数越大。当φ=常数，表示垂直于xy组成的平面且此平面过z轴。
通过图1-2-2（c）可知球坐标系中一点是由三个面（球面、锥面和平面）两两垂直产生的。
球坐标系上一点的单位矢量都垂直于组成这个点的三个面中的一个面，并且方向指向能使坐标值增加的方向。单位矢量er是沿半径r的方向，箭头指向外且垂直于半径为r的球表面，存在于φ=常数和θ=常数的面中。单位矢量eθ垂直于圆锥表面，位于φ=常数的平面上并且与球面相切，方向为沿着“经度”线延伸到“南”。第三个单位矢量eφ与在圆柱坐标中eφ相同都是垂直于φ=常数的平面且与锥体和球体相切，方向指向东。
如图1-2-2（c）所示，三个单位矢量相互垂直且通过er×eθ=eφ来定义右手坐标系。(www.chuimin.cn)
将直角坐标系的坐标值与球坐标系的坐标值进行互换的公式如下：
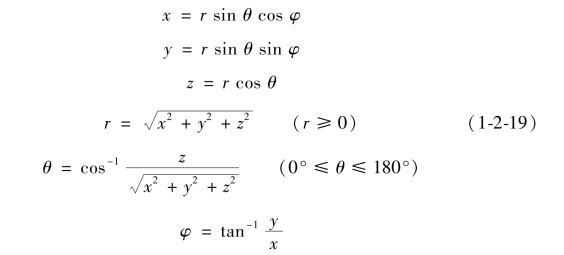
半径变量r是非负的，θ限制在0°到180°的范围内。
有关工程电磁场基本原理的文章
- 详细阅读
-
圆柱坐标系-工程电磁场基本原理详细阅读
直角坐标系是常用的一类坐标系，但对于一些对称性问题时，需要一种更加便利的坐标系，两个常用坐标包括圆柱形坐标和球形坐标。如图1-2-2所示，定点P也可用常规的直角坐标系来表示。一般圆柱坐标系上的三个平面都可表示坐标系中的任何点，但若点位于z轴上，那么一个面即可。图1-2-2三种坐标对比除此之外需在圆柱坐标系中定义三个单位矢量eρ、eφ和ez，单位矢量同样是两两相互垂直的关系。圆柱坐标系和直角坐标系是一一对应的关系。......
2023-11-19
-
基本原理和特点：基本原理详细阅读
功率密度小于104～105W/cm2为热传导焊，激光辐射加热待加工表面，表面热量通过热传导向内部扩散，此时熔深浅、焊接速度慢；功率密度大于105～107W/cm2时，金属表面受热作用下凹成“孔穴”，其冶金物理过程与电子束焊极为相似，形成深熔焊，具有焊接速度快、深宽比大的特点。......
2023-07-02
-
基本原理和特点 of 7.3.1详细阅读
图7-42 TIG焊焊接过程示意图2.非熔化极气体保护焊的特点主要优点1）能够实现高品质焊接，得到优良焊缝。TIG焊时采用的保护气体没有脱氧去氢的能力，因此对焊前的除油、去锈及去水等清理工作要求严格。......
2023-07-02
-
基本原理与特点：深入解析详细阅读
无论是在车间内，还是在野外施工现场均可采用。完成一条焊缝需要不断更换焊条，对厚板需要开坡口进行多层焊接，这不仅造成焊条的浪费，提高了焊接成本，而且降低了生产率。......
2023-07-02
-
弧焊电源的基本原理和特点详细阅读
最常用的弧焊电源有机械式控制和电子式控制弧焊电源。机械式控制的基本原理如图1-1-15a和式所示，不再重复。它的质量是弧焊电源可靠性和性能好坏的决定性因素之一。从基本原理上，可把它看成音响设备的末级功率放大器。图1-2-1 电子控制式弧焊电源基本原理框图电子控制系统的任务是与电子功率系统配合，控制调节静、动特性以及焊接参数、波形和时序。......
2023-06-25
-
基本原理与特点：探究7.2.1详细阅读
由于焊接时电弧掩埋在焊剂层下燃烧，电弧光不外露，因此称为埋弧焊。埋弧焊原理如图7-13所示。这是因为埋弧焊不能直接观察电弧与坡口的相对位置，故必须保证坡口的加工和装配精度，或者采用焊缝自动跟踪装置，才能保证不焊偏。......
2023-07-02
-
灰色预测的基本原理及模块构成详细阅读
灰色预测是建立一种以灰色模块为基础的描述系统动态变化特征的方法。灰色系统理论把原始数据经过累加生成的新数据序列，在几何意义上称为“模块”。很显然，时间就是指序列在时间、数据的二维平面上所做的连续曲线与其底部的总称，预测下限并将由已知数据列构成的模块称为白色模块;而由白色模块建模外推的未来模块，即预测值构成的模块，称为“灰色模块”，见图9.6。......
2023-06-30
相关推荐