图1-1-1二矢量之和如图1-1-1所示两个矢量的A与B的和，易得A+B=B+A，由此可知，矢量加法遵循交换律的同时也服从结合律。图1-1-2二矢量之差矢量的乘法1）标量与矢量的乘积矢量乘以标量，结果矢量的大小发生改变，方向并未发生改变。图1-1-3二矢量点乘图1-1-4二矢量叉乘......
2023-11-19
圆柱坐标系-工程电磁场基本原理
【摘要】：直角坐标系是常用的一类坐标系，但对于一些对称性问题时，需要一种更加便利的坐标系，两个常用坐标包括圆柱形坐标和球形坐标。如图1-2-2所示，定点P也可用常规的直角坐标系来表示。一般圆柱坐标系上的三个平面都可表示坐标系中的任何点，但若点位于z轴上，那么一个面即可。图1-2-2三种坐标对比除此之外需在圆柱坐标系中定义三个单位矢量eρ、eφ和ez，单位矢量同样是两两相互垂直的关系。圆柱坐标系和直角坐标系是一一对应的关系。
直角坐标系是常用的一类坐标系，但对于一些对称性问题时，需要一种更加便利的坐标系，两个常用坐标包括圆柱形坐标和球形坐标。每个坐标系都适合应用在不同的环境中，因此需要深入了解才可灵活的应用。
圆柱形坐标系是三维解析几何的极坐标（图1-2-2（b））。在极坐标系中，在空间上给定一点P，原点与定点P连成的直线在xy围成的平面上的投影的距离为ρ，与x轴的夹角为φ。z是定点P垂直于xy所在平面的垂直距离。
不同于直角坐标设置的三个轴，将坐标系中任意一点视为三个相互垂直面的交点。这些面分别是圆柱面（ρ=常数），底平面（φ=常数）和顶平面（z=常数）。如图1-2-2（b）所示，定点P也可用常规的直角坐标系来表示（x=常数，y=常数，z=常数）。一般圆柱坐标系上的三个平面都可表示坐标系中的任何点，但若点位于z轴上，那么一个面即可。
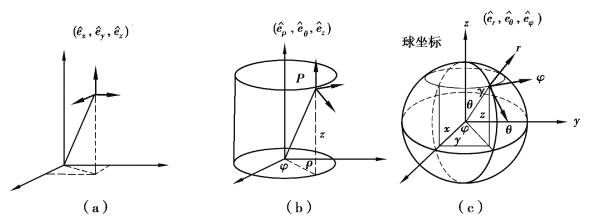
图1-2-2 三种坐标对比
除此之外需在圆柱坐标系中定义三个单位矢量eρ、eφ和ez，单位矢量同样是两两相互垂直的关系。单位矢量服从右手定则，即eρ×eφ=ez，且可知拇指、食指和中指分别指向ρ、φ和z增加的方向。(www.chuimin.cn)
圆柱坐标系和直角坐标系是一一对应的关系。由1-2-17可知
换言之可用x、y、z表示圆柱坐标系中的坐标。
有关工程电磁场基本原理的文章
- 详细阅读
-
工程电磁场基本原理：通量与闭合曲面的关系详细阅读
曲面S是大小为S、方向沿曲面的垂直方向dS的曲面。图1-5-2矢量场的通量图1-5-3矢量场的闭曲面通量则矢量场F穿过有向曲面元dS的通量为：而曲面S上各面元dS叠加，分别得开曲面和闭曲面的通量：通量的物理意义：闭合曲面的通量从宏观上建立了矢量场通过闭合曲面的通量与曲面内产生矢量场的源的关系。......
2023-11-19
- 详细阅读
-
电位与静电场的环路定理：工程电磁场基本原理详细阅读
电场强度定义为单位试验电荷在电场中所受的电场力。如图2-2-1所示，环量的意义是将单位正电荷沿闭合路径移动一周，电场力做的功，环量的表达式为：图2-2-1电场的环量如图2-2-2所示，点电荷的电场的表达式如下：由此可以得出结论，W仅与q0的始末位置有关，与路径无关。图2-2-4环路定理示意图图2-2-5电位差示意图如图2-2-5所示，静电场是保守场，静电场力是保守力。则这个公式的物理意义为把单位正试验电荷从点a移到无限远处时静电场力作的功。......
2023-11-19
-
球坐标系的基本原理及特点详细阅读
半径r与z轴所夹的夹角为θ，当θ为常数时，在球形坐标系构成了两个面，一个是锥面，一个是球面。通过图1-2-2可知球坐标系中一点是由三个面两两垂直产生的。第三个单位矢量eφ与在圆柱坐标中eφ相同都是垂直于φ=常数的平面且与锥体和球体相切，方向指向东。如图1-2-2所示，三个单位矢量相互垂直且通过er×eθ=eφ来定义右手坐标系。......
2023-11-19
-
电流与电流密度-工程电磁场原理详细阅读
图3-1-1电流与电流面密度矢量但是由于电流定义的局限性，因此需引入电流密度J来描述电流的分布情况。从电流密度J定义可以求出流过任意面积S的电流强度。一般情况下，电流密度J和面积dS元的方向并不相同。......
2023-11-19
-
工程电磁场中的高斯通量定理应用详细阅读
高斯用数学公式表达上述结论：静电场中通过一个任意闭合曲面的电通量值等于该曲面所包围的所有电荷电量的代数和∑Ιqi除以ε0，与闭曲面外的电荷无关，称为高斯通量定理。b.穿过该高斯面的电通量容易计算。c.计算电通量和高斯面内所包围的电荷的代数和，最后由高斯定理求出场强。图2-3-3高斯面内的点电荷系图2-3-4对程序分析示意图以图2-3-4为例，应用高斯通量定理求解球形面场强的计算过程如下：......
2023-11-19
-
基因工程技术简介及基本原理详细阅读
（一）基因工程介绍和基本原理基因工程是现代生物学研究的重要手段，它是综合运用多项现代生物技术，实现DNA分子人工定向改造的一种技术方法。基因工程除了可以构建各种重组质粒外，还可以对基因组DNA进行改造，在基因组的特定位置点删除、替换、插入外源基因序列，构建各种基因工程菌。基因工程技术涉及以下步骤：从生物体的基因组中分离目的DNA序列（基因）。这通常包括DNA的纯化技术、酶促消化或机械切割等。......
2023-11-06
相关推荐