揭秘被遗忘的数学课-被遗忘的数学课

2023-11-19 理论教育版权反馈

【摘要】：所有科学的发展都以一条假设为基础：宇宙在以一种可以为人类所理解的方式运转.在纷繁多彩、令人诱惑的自然现象背后，隐藏着某种简洁的规律，人类思维能与这种规律协调相符，多亏有了数学，人类正是通过数学来研究探索宇宙运行的基本法则.数学是科学发展的基石.在许多同学们的眼里，阿基米德、牛顿是以物理学家的形象出现的，殊不知他们还是最杰出的数学家.今天我向大家再重点介绍一个人物，他也是一位物理学家，但他同时也应该

所有科学的发展都以一条假设为基础：宇宙在以一种可以为人类所理解的方式运转.在纷繁多彩、令人诱惑的自然现象背后，隐藏着某种简洁的规律，人类思维能与这种规律协调相符，多亏有了数学，人类正是通过数学来研究探索宇宙运行的基本法则.

数学是科学发展的基石.在许多同学们的眼里，阿基米德、牛顿是以物理学家的形象出现的，殊不知他们还是最杰出的数学家.今天我向大家再重点介绍一个人物，他也是一位物理学家，但他同时也应该是最懂得数学力量的人物之一，他的名字叫伽利略.

1564年2月15日，伽利略在意大利比萨市出生，1581年听从父亲的建议进入比萨大学学习医学，然而，年轻时他完全被阿基米德的著作所吸引，他曾说凡是阅读了阿基米德著作的人都会有一种高山仰止的感觉，与阿基米德相比，其他所有人的思想都不值一提，当然，伽利略当时并没有意识到，他本人却正是那些为数不多的能与这位古希腊数学大师相提并论的人物之一.

科学的历史是由不计其数的推测、假设、模型在正确与错误之间经历了无数次起起落落的故事构成，有些看起来十分精妙的理论最终也可能被证实是错误的，或者走入了死胡同.即使是人类历史上最聪明的几个头脑所发现和总结的“定律”也免不了不断地被质疑或修正，而解决问题的往往是数学.

1589年，25岁的伽利略被任命为比萨大学的数学系教授，他把研究方向和研究方法主要集中在数学领域，伽利略很清楚，在任何学科建设中，如果该理论无法精确地用数学语言表述，就不可能评估它的意义.

两千多年前，伟大的亚里士多德声称，质量大的物体下落的速度要更快一些，物体下落的速度与它的质量成正比.人们日常的生活经验似乎也能说明这条定律是正确的，一块砖确实要比和它在同一高度下落的一根羽毛更早落地，亚里士多德没有精确、定量地验证过他的表述是否正确，他也曾试图总结出这种运动的数学公式，但没有成功.亚里士多德关于物体运动的这条错误定律，被人类接受并得到广泛认可的时间竟然长达近两千年，这是“完美风暴”的一个典型的例子，几种不同力量交织在一起创造了这样一条不容置疑的教条.

首先，在没有精确测量的环境下，亚里士多德的运动定律看上去和以人们经验为基础的常识相一致，这自然就会使人们很轻易地就接受它，其次，亚里士多德有着几乎无人能与之匹敌的崇高声望，是一位学术权威，现代西方文明最主要的奠基人.在这样的巨人面前，很少有人能鼓起勇气挑战他的权威，在某种程度上，可以说是亚里士多德教给了我们思考的方法，正是亚里士多德第一次将正式的逻辑学引入我们的思维，他那著名的三段论方法是如此的深入人们的骨髓之中.

伽利略（意大利，1564—1642）

亚里士多德这条不正确的运动定律能保留这么长时间的第三个原因是，基督教将亚里士多德的这条定律作为教会官方的正规信仰广泛流传，这使得那些试图质疑亚里士多德理论的人望而却步，教会的力量是如此的强大，想想布鲁诺的悲剧就使人不寒而栗.

伽利略第一个公开站出来，指出在这个问题上亚里士多德完全错了，伽利略所用的武器正是数学的两大法宝：逻辑和定量描述.

伽利略的思想实验过程是这样的：假设我们手头有两个质量不一的物体，现在，我们把它们绑在一起，从高处把这个组合体扔下来，那么，它们下降的速度比其中任何单独一个下落时快多少？一方面，很明显这个组合体肯定要比这两个物体任何单独的一个质量都大，根据亚里士多德的定律，它下降的速度应当比质量大的那个物体单独下落时还要快；但另一方面，因为轻重不一的两个物体被捆在一起，质量小的物体会拖累质量大的物体下降时的速度，也就是说会使重的那个物体下落速度变慢，同样根据亚里士多德的观点，绑在一起后下落的速度应当是比质量大的那个物体单独下落速度要小，这样，这两个速度值都是从亚里士多德的定律推导出来的，但这是两个相互矛盾的结论.

事实上，今天我们都知道羽毛比砖头下落要慢的唯一原因是羽毛承受的空气阻力更大.伽利略通过他那著名的比萨斜塔实验证明，如果不计空气阻力，物体下落的时间取决于它的高度，而与它的质量无关.在同样的高度，两个物体同时放开，两者将会同时落地，因为伽利略成功地用数学关系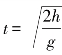 pagenumber_ebook=226,pagenumber_book=218 定量地描述了这个结论.

伽利略的公式 pagenumber_ebook=226,pagenumber_book=218 是第一个用来描述自然现象的数学公式，后来，这种用数学元素定量地对自然的描述理论便发展为人们所称的物理学.

以这种运用数学思想对事物进行定量描述的方法彻底改变了人们看待世界的方式.以前人们只通过日常话语定性地描述自然现象，这种描述可能十分模糊——你可以说某个物体正在下降，但无法指出其落地的时刻与其他量的数学关系，借助于数学语言，人们不仅可以更加准确地描述自然，同时还能够预测出其未来的改变.(www.chuimin.cn)

伽利略还是第一个破解出钟摆摆动之谜的人.伽利略17岁的时候，有一次在比萨大教室做弥撒，无聊之时，伽利略抬头盯着天花板发呆，忽然看到天花板上一盏吊灯随着穿堂而过的微风轻轻摇摆.伽利略记下吊灯从一端摆至另一端所用的时间（那时他只能用自己的脉搏来记录这种摆动结果），有了一个重大发现：吊灯摆动一次所需的时间似乎和摆动的幅度并无关联，换句话说，增加或减小摆动幅度，摆动一次所需的时间基本毫无变化.

伽利略通过进一步的研究，成功地得到了钟摆的摆动时间T和钟摆长度的数量关系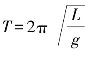： pagenumber_ebook=227,pagenumber_book=219 ，这也是一项十分重大的发现，它进而催生了用来记录时间流逝的钟摆.

自伽利略研究自由落体和钟摆现象以来，物理学家已创造出成千上万个公式，来描述自然界中的各种行为状态，这些公式构成了现代科学的基础，并被人们称之为自然法则.在数学的帮助下，人类得以把握我们当今居住其间的复杂世界，工程师依靠公式来确保桥梁不会坍塌，以及飞机平稳穿行云端……

科学哲学家亚历山大·科瑞（1892—1964）曾经评价道，伽利略在科学思想上的革命可以提炼为一项本质原则：数学是科学的基本原理.当亚里士多德学派沉醉于定性描述自然，伽利略则坚持主张解密宇宙术语的关键是相关的数学和几何模型.“大自然的这本书是用数学语言来写的”正是伽利略的信条.

伽利略于1642年去世，同一年牛顿诞生了.

牛顿用抽象的数学公式来描述他的理论，自然规律被精确地表述成如水晶般清晰的数学关系.正是数学这种内在的精确和深刻，使牛顿的发现由一般的理论上升到不可动摇的自然规律的高度.

牛顿利用他的一整套数学工具所做出的伟大业绩是超乎一般人想象的，这位天才出生的那一年与伽利略离开人世是同一年，这也许是历史的巧合，他用数学公式系统地阐述了力学基本原理，破译了行星的运动规律，并为解释光和色彩现象的本质建立了理论基础，这些都得益于牛顿发明的秘密武器：微积分.

与此形成鲜明对比的是，胡克的理念虽然在很多方面也体现了独创性，但整体上而言，大多是直觉、推测和猜想的集合.

胡克是一位有丰硕成果的物理学家和生物学家，也是牛顿一生中科学上最大的对手.胡克曾在多种场合中指控牛顿窃取了他的思想，一项是在光学领域中某个理论，还有一项就是引力理论.在研究行星的运动方面，胡克声称自己早就已经推断出引力与距离的平方成反比这一规律，但他还不能从这个推断中构建出一个完整的数学模型.1684年，哈雷决定问牛顿一个至关重要的问题，以判断这对冤家的是是非非，哈雷问：能根据行星引力与距离平方成反比这一规律得出行星形成的轨道是什么样子吗？让他感到震惊的是，牛顿脱口而出是个椭圆，并且告诉他早在几年前他就证明出来了，牛顿证明了大部分天体运动的轨迹是圆形或椭圆形，证实了开普勒的所有行星运动定律.哈雷对牛顿的工作十分推崇，他极力劝说牛顿将他所有这些令人难以置信的发现结集出版，这促使划时代的《自然哲学的数学原理》的最终诞生.

对牛顿的数学和科学思想影响最大的一本书，正是笛卡尔的《几何》，牛顿在1664年读到了这本书，之后他又反复地读了好几遍，直到“完全掌握了这本书”.函数的概念所提供的灵活性，以及其中的自由变量为牛顿提供了无限的可能.不仅是解析几何，还有与之相关的笛卡尔在函数、切线和曲线方面的探索，这些为牛顿创建微积分铺平了道路.

自然界中的变化可用数学过程来描述，所发现的物理定律都有一个相似的特征，它们都以方程的形式来表述，自牛顿以来，数学物理学的策略大多是用各种微分方程来描述变化的事物，然后求解方程.

用数学与物理科学发展的关系来说明数学与客观实在的关系，展示了数学在研究自然时的作用，从《数学与物理世界》一书中人们可以看到数学是怎样成为以及为什么会成为科学理论的核心的.从欧氏几何对物理空间的描述，圆锥曲线理论应用于近代天文学理论，微积分对于近代科学发展的决定性影响，直到麦克斯韦的电磁学微分方程组、广义相对论所利用的黎曼几何，这些似乎都在证实，而且在不断地证实，数学才是解密自然的钥匙.

M.克莱因认为，数学不仅为人类认识自然、把握自然提供了最重要的方法，而且还指明了科学发展的方向.数学与其他科学的区别还在于它能自由地创造自己的世界，而无须顾及这种自由创造是否“有用”，虽然说圆锥曲线论、群论、黎曼几何在刚产生时完全属于数学上的一种自由创造，但是后来这些理论在科学研究中都发挥了巨大的作用，数学除了一直在给予人类征服自然的神奇力量，数学还是科学的灯塔.

揭秘被遗忘的数学课-被遗忘的数学课

相关推荐