数学的普遍性与花瓣间奇特模式

2023-11-19 理论教育版权反馈

【摘要】：人们认为，即使他们不能了解上述信息，任何有智能的外星人都应该能够理解简单的数学模式：数学具有高度的普遍性.外星人和我们一样，可以计数1，2，3……里所展示的内涵模式.最简单的数学对象是数字，自然界最简单的模式是数字的模式.一个有趣的例子是，在花的花瓣中就存在着一个奇特的模式，几乎所有的花，花瓣的数目都是如下奇特序列的数字中的一个：3，5，8，13，21，34，55，89……

到公元前500年左右为止，数学其实就是有关“数”的一门学问.在古代文明中，数学所包括的，几乎都以算术为主，它大部分属于应用上面的一些东西，例如，我们在古代数学文献中经常会看到“对一些数字这样做，那样做，你将会得到答案”诸如此类的一些特色.

从大约公元前500年到公元300年的这一时期，数学大大地扩张了，超越了研究数的范围.这一时期是属于希腊数学的时代，古希腊的数学家主要关心的是几何.他们按几何方式，将数字视为线段长的度量，而平方数为面积的度量，立方数为体积的度量，特别是当他们发现正方形的对角线“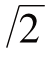 pagenumber_ebook=214,pagenumber_book=206 ”这样一个“怪物”，作为“万物皆数”中的数（整数）都不能表示时，对数的研究基本上就停滞下来了.由于他们强调几何学，所以数学不只研究“数”，而且也是有关形状的学问.

值得一提的是，幸亏有希腊人的理性思想，数学才进入研究领域，而不再只是度量、计算和会计等功利的工具，古希腊人对数学的实际应用不大感兴趣，而把数学看作一种对知识、对真理的探求.泰勒斯引入一种观念：数学上陈述的结论，都必须以一个形式的论证逻辑地证明出来，这一创新标志着定理——数学基石的诞生，这一理性思想的进程经由毕达哥拉斯到欧几里得《几何原本》问世时达到了巅峰.

希腊人之后，欧洲进入黑暗的中世纪时期，这时数学在阿拉伯世界和东方（主要是中国和印度）取得进展，代数学得到长足的发展.直到17世纪，革命导师恩格斯给数学下了个定义：数学是研究数量关系和空间形式的一门学科.

17世纪是一个英雄辈出的世纪，就数学而言，17世纪之前的数学与17世纪之后的数学正是我们中学生与大学生数学学习的分水岭.在此之前，数学大都局限于计算、度量和形状描述的静态议题上，随着解析几何的建立，牛顿和莱布尼茨引进处理运动和变化的技巧发明微积分之后，数学家终于可以研究天上的行星与地上的落体的运动，机械的运转，液体的流动，气体的扩散，电力和磁力，研究动植物的生长，流行病的传播以及利润的波动等穷尽所有变化的情形.在牛顿和莱布尼茨之后，数学变成了研究数量、形状、运动、变化以及空间的一门学问.

微积分为人类的生活和科技进步带来巨大的力量，同时，数学本身也得到飞速发展，数学可以被分为大约十几个分支，数论、几何、代数、分析和拓扑学等，同时，数学家对数学理论的研究也越来越重视，他们不光关注应用，还迫切地寻找微积分巨大威力的背后，究竟隐藏着什么东西，纯数学的发展使现代数学进入全新的领域.

20世纪，数学研究的壮大可用一个词来形容：知识爆炸.打个比方，1900年，世界上所有的数学知识可以塞进约1000本书里，时至今日，许多新的分支纷纷涌现，新的理论雨后春笋，也许需要用10万卷书才能包罗一切已知的数学知识，以至于没有任何一位数学家能通晓所有的数学分支领域.1912年，去世的法国数学家亨利·庞加莱被认为是最后一位“数学通才”.

基于数学活动如此迅速成长这一事实，如今，一个为大部分数学家所认同的有关数学的一个最好的定义——数学是研究模式的科学——终于出现了，出自索耶在1955年所写的《数学的序幕》一书中.

“模式的科学”简洁、精练，但我们一般的人还需要在不断的数学学习中才能慢慢地体会和理解这句话的含义，一个略为详尽的扩充定义是：数学是规律、模式、结构与逻辑关系的科学.然而，由于数学家在这里所说的“模式”这个字眼其实已经包含了扩充意义里的所有内容，“模式的科学”已经把该说的统统都说了，一旦你确切地体会了数学家心目中“模式”的含义，以及他们如何对其进行研究，就会感觉到这个定义的巧妙之处.(www.chuimin.cn)

当“先驱者号”和“旅行者号”宇宙飞船驶向天际，它们携带了一些信息，想要传送给宇宙的外星人.人们将氢原子，标明我们所居住星球的太阳系的概要图案以及站立于飞船前裸体男人和女人的线条图画，全都刻在金属板上，此外飞船上还携带了各种大自然的声音、音乐和科学影像的记录.

但外星人接收者是否可以破解这些信息呢？人们认为，即使他们不能了解上述信息，任何有智能的外星人都应该能够理解简单的数学模式：数学具有高度的普遍性.外星人和我们一样，可以计数1，2，3……他们一定会读懂如图案X，XX，XXX，XXXX……里所展示的内涵模式.

最简单的数学对象是数字，自然界最简单的模式是数字的模式.一个有趣的例子是，在花的花瓣中就存在着一个奇特的模式，几乎所有的花，花瓣的数目都是如下奇特序列的数字中的一个：3，5，8，13，21，34，55，89……这些数字有一个明显的模式：每一个数字都是前两个数字的和.

除了数字模式之外，还存在着几何模式.吸引数学家的主要是一些简单的形状，如三角形、四边形、五边形、六边形、圆形、椭圆形、螺线形、立方体、球体、锥体等，这些形状都可在自然界中找到，例如彩虹就是许多圆的集合体，每个圆有一种颜色，我们通常看不到完整的圆，见到的只是一段弧，但从大气中看到的彩虹可以是完整的圆，你还可以从池塘里的波纹，动物的眼睛以及蝴蝶翅膀上的花斑中见到圆.

除了形体模式之外，还存在着运动模式.开普勒对他同时代的丹麦天文学家第谷·布拉埃所做的大量天文观测结果进行分析，终于找到了行星行为中的数学模式：太阳系的6颗行星（当时只知道金、木、水、火、土、地球）的公转周期（绕太阳运转一周所需的时间）与它们和太阳的距离有关，即距离的平方除以公转周期的立方是一个常数.这个数虽然不是一个特别雅致的数，但它对所有6颗行星而言都相同，这一数学模式是通往牛顿万有引力理论的关键步骤之一.

微积分的发明（处理运动和变化的模式）改变了地球的面貌，物理学家用变化率解释自然现象的规律，数学、声学、光学、流体动力学、弹性力学、电学、磁学等学科得到飞速的发展，人们利用这些知识来认识自然和预言自然的一些行为方式，取得了巨大的成功.

以上所列举的一些例子，都属于“确定性”的模式，最后，还存在着另一套自然模式，它只是在近代才慢慢被人类所认识和掌握，这是自然无处不在的模式——无规和无形，新的数学理论的发展，使自然之模式许多难以捉摸的方面也逐渐被揭开.

概括来说，数学研究的模式可以是静态的或动态的，定量的或定性的，纯粹应用或纯粹理论的；可以是真实存在的或想象的；也可以是确定性的或不确定性的.它们来自我们周边的世界，来自时空深处，也来自我们人类心智的活动，不同种类的模式引发了不同的数学分支，而我们知道，自然的模式美丽且无穷无尽，每一个自然之模式都是一个谜，数学在帮助我们解谜方面必不可少，成就斐然.数学研究逐渐成为一种兴旺且无所不在的活动，数学随着我们对自然认识的不断加深而发展.

数学的普遍性与花瓣间奇特模式

相关推荐