黎曼1859论文：解析误差项和函数的关键非平凡零点

前面我们已经说过，高斯首先发现素数的密度函数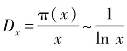，用文字描述就是π（x）与之间的相对差随着x越来越大而逐渐减小到0，这个结论被称为素数定理.

后来的数学家发现，用函数作为对π（x）的估计，其近似程度比更好，Li（x）是一个更强的估计，Li（x）～π（x）被称为“豪华版”的素数定理.

高斯也未能证明这个结论，它们都只能说是猜想.

黎曼在高斯猜测的基础上进行更深入的研究.在素数定理未能被证明之前，高斯的这个猜想是数学上最大的谜.

1849—1850年间，圣彼得堡大学的一位年轻讲师帕·利·切比雪夫发表了关于素数定理的两篇卓越的论文，切比雪夫证明了：如果对于某个固定的数C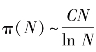，，那么C一定等于1.

切比雪夫的第二个结果：π（N）与的差距上下不可能超过10%.

1881年，美国约翰·霍普金斯大学的西尔维斯特改进了切比雪夫的限度范围，从10%降到4%.

他们完全没有用复变函数来得到这些结果，数学家说这些方法是“初等的”，他们对素数分布的研究还局限在实分析手段上，黎曼在他1859年的论文中，把复变函数的强大功能作用于他正在研究的问题，是对素数分布研究的重大突破，而正是这个突破为素数定理的最终证明铺平了道路.

这件事最终在高斯提出他的猜想近100年以后的1896年，由法国数学家阿达马和比利时数学家瓦莱·桑各自独立地给出了证明，终于完成了自高斯以来数学界的一个重大心愿.值得注意的是，这一年距离黎曼发表他那著名论文的1859年也已过了37年.

复变函数方法在素数定理的证明中起了决定性的作用，以至于当时的人们认为素数定理不存在初等证明（即不用黎曼的复变函数方法的证明），不过，这一点在1949年被挪威数学家塞尔伯格（AtLesLberg，1917—2007）与匈牙利数学家保罗·鄂尔多斯（paulErdos，1913—1996）推翻，他们找到了素数定理的初等证明，在他们之后，更多的初等证明也被陆续发现.

黎曼1859的论文与证明素数定理有直接的关联，如果黎曼假设成立，PNT就能作为它的推论而成立，然而，这个假设是比PNT强得多的结论，后者可以从更弱的前提来证明，黎曼的论文对证明PNT的主要意义在于它提供的强有力的工具.

素数定理被成功地证明，黎曼假设成为数学界最重要的问题.

从1896年高斯猜想成为素数定理起，人们知道从数学上可以毫无疑问地确定π（x）～Li（x），所有人的注意力都集中在那个波纹号上，只要x无限制地越来越大，π（x）就相应地越来越接近于Li（x），但这个接近的本性是什么？黎曼1859的论文给出了误差项的精确表达式，这个表达式涉及了ζ函数的所有非平凡零点，因此，理解这个误差项的关键以某种方式隐藏在这些零点之中.

零点在哪里？黎曼猜测它们都在临界线上（复平面上的直线）.

数学家开始向这个猜测发起进攻.他们首先从欧拉乘积公式推出，非平凡零点全都位于0≤Re（s）≤1的区域内，这个区域被称为临界带，如图9-4（1）.

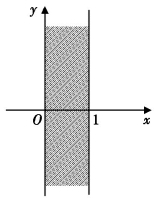
图9-4（1）

证明素数定理的阿达马、普森同时也证明了非平凡零点都位于复平面0＜Re（s）＜1的区域内，虽然这个结论只是除去了临界带的边界，但也是一个了不起的进展.

玻尔-兰道定理说，包含临界线的无论多小的带状区域内都包含了几乎所有的非平凡零点，这句话有点意思，它清楚地显示了临界线在非平凡零点分布中的独特的地位，临界线是非平凡零点的汇聚中心（如图9-4（2）），这也是一个沉稳而扎实的进展，数学家们正一步步地逼近着临界线.

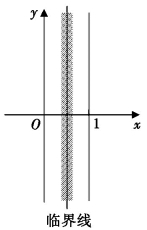
图9-4（2）

然而，再逼近也是一种逼近，毕竟没有到达临界线.

不同的数学家根据各自的数学倾向，以不同的方式对这个问题产生迷恋，存在多条思路的发展——以不同的方法研究这个假设，每种方法都源自某一个个人，再由其他人推进，这些思路有时交叉，有时又互相纠缠，例如，有一个是计算的思路，一路的数学家们开始着手于计算，他们试图一个一个地去抓捕那些零点.

黎曼1859年的那篇论文中有好几个命题，它们被高度浓缩在区区八页纸的表述中，这些命题个个令人头疼，如果那些非平凡零点容易计算，那倒也罢了，可怕的是它们也个个都不是省油的灯.

直到1903年（1859年后的第44个年头），丹麦数学家格拉姆才首次公布了黎曼ζ函数的前15个非平凡零点的计算结果（这里以虚部为正的零点开始计数，虚部为负的零点与虚部为正的零点关于实轴对称）.

黎曼ζ函数前15个非平凡零点

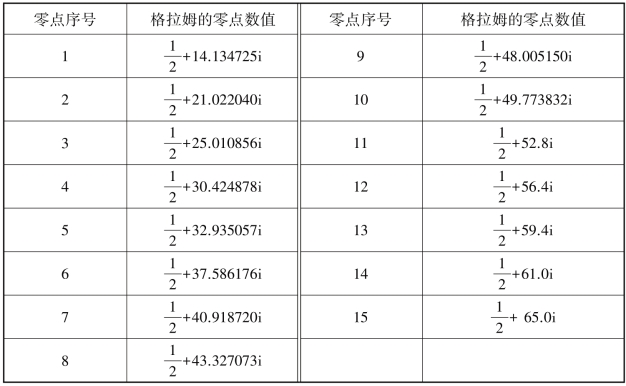
44年来，这是数学家们第一次拨开迷雾，实实在在地看到黎曼ζ函数的非平凡零点，看到那些蕴藏着素数分布规律的神秘家伙，它们都乖乖地躺在44年前黎曼画的那条奇异的临界线上.格拉姆的计算使用的是18世纪30年代发展起来的欧拉-麦克劳林公式，在只有纸和笔的年代里，这里面的计算是非常困难的，格拉姆用了好几年的时间才完成前15个零点的计算，即使这样，他在后五个零点的计算精度上仍不得不有所放弃.

在格拉姆以后，贝可隆于1914年把对零点的计算推进到了前79个零点，再往后，哈代、李特尔伍德和美国数学家哈钦森在计算方法上做了一些改进，1925年，人们计算出了前138个零点.

1932年，西格尔通过对哥廷根图书馆黎曼遗稿的深入研究，发现黎曼在他为1859年论文所做的后台工作中，提出了计算零点的一个好得多的方法，而且他自己使用这个方法计算出了最初的三个零点.而这在1859年的论文中丝毫没有透露，它完全隐藏在未发表的遗稿中.西格尔根据黎曼的思想，总结出了一个计算零点的公式，现称黎曼-西格尔公式，这个公式对于黎曼ζ函数非平凡零点的大规模计算来说，要比欧拉-麦克劳林公式有效得多.

黎曼-西格尔公式发表后大约过了几年，哈代的学生、英国数学家蒂奇马什成功地计算出了黎曼ζ函数的前1041个零点，在计算方法上，他用黎曼-西格尔公式取代了欧拉-麦克劳林公式，在计算手段上，他运用了英国海军部的一台打孔式计算机，这是数学家们在零点计算上首次使用机器计算取代传统的纸和笔.

著名的英国密码专家图灵（AlanTuring，1912—1954）对计算机及人工智能做了深入的研究，图灵在传统的数学领域内也有相当深厚的功力，对黎曼假设非常着迷，第二次世界大战以后（20世纪50年代初），图灵终于研制出了自己的机器（图灵机），于1953年成功计算出了前1104个零点，不过，图灵试图找到一个反例的计划未能实现，黎曼假设在他计算所及的范围内岿然不动.

随着计算机技术的发展，零点的计算步入了快车道，零点的计算不断刷新原有的记录，计算机的威力大大超过了人们的想象，1982年特里奥计算出了前307000000个零点，2004年古尔登与戴克尔验证了黎曼ζ函数前十万亿（1013）个零点全部位于临界线上.

对其他学科而言，这么强有力的证据已经足够了，“假设”早就变成“定律”了，但对数学而言，没有被证明的“假设”永远是“假设”，成不了定理，通过计算来验证，对黎曼假设来说充其量也只是有着一定的心理支持作用，更有甚者，就是这点心理支持作用很多数学家也很不以为然.

其实，早在1914年，两位英国大佬“就在”那里笑了.

1914年以前的零点计算，涉及的数目少得可怜，哈代一个零点也没算出来，但他用分析的力量证明了“哈代定理”：黎曼ζ函数有无穷多个非平凡零点位于临界线上.

哈代定理永久性地超过了后世所能给出的任何具体的数值计算结果，因为无论用多么高明的算法，无论用多么强大的计算设备，再大的数目相对于“无穷”来说都只是一个“零”.

哈代定理通过对这些“无穷多个零点”的存在性证明，为黎曼假设提供了强有力的支持，无疑是一个了不起的成就.那么，它离目标还有多远呢？从字面上看，黎曼说黎曼ζ函数所有（无穷多个）非平凡零点都在临界线上，而哈代说确实有无穷多个非平凡零点位于临界线上，两者好像已是一回事，可惜的是，“无穷”这一概念正是数学中最微妙的概念，两个“无穷”之间不仅是不相同的，简直可以说它们相距要多遥远就有多遥远，甚至相距无穷远.

数学就是这么奇妙，计算零点的人会想，就算哈代一劳永逸地超越了我们，但零点的计算还是非常有价值的，如果计算的零点在临界线上，就是对黎曼假设的支持，如果运气好，碰巧发现有一个零点不在临界线上，那不也算解决了黎曼假设（黎曼假设不成立）吗？

哈代的兄弟，李特尔伍德又笑了.

在关于Li（x）～π（x）的这个绝对误差项的估计上，在很大的数的范围内，人们都非常有把握地说，绝对误差Li（x）-π（x）总是正的，以至于天才的高斯在进行自己的研究时，也确信情况总是如此，这使得人们猜测，Li（x）不仅是素数分布的渐近形式，而且还是π（x）的严格上界，但是，李特尔伍德1914年的论文引起了轰动，因为他证明了情况并非总是如此：存在这样的x，使得π（x）大于Li（x）.

李特尔伍德1914的成果：(www.chuimin.cn)

Li（x）-π（x）从正变为负，再从负变为正，反复无穷多次.

令人瞠目结舌的东西还在这里，李特尔伍德的学生后来搞出来了，π（x）第一次超过Li（x）——出现在很远很远的地方，最近的结果在x=1.39822×10316之前，并且很可能就出现在这个数上.

即使现在的计算机算到十万亿（1013）个零点，按李特尔伍德的意思，它们其实都还远远没有涉及真正有价值的区域.在数学上，计算机的工作仅仅告诉我们，如果真的存在不位于临界线上的零点，那么它将是一个很大很大的数.因为它是如此之巨大，可能任何计算机都不能处理——也许永远都不能处理！

对于通过零点的计算来研究黎曼假设，哈代说，验证再多的零点在临界线上也无用，李特尔伍德说，如果有反例，那个反例可能出现在你永远也无法通过计算到达的地方，无论你用什么办法，就是计算机也解决不了问题.

那么，抓捕零点是不是就没有意义了呢？

显然不是，黎曼假设还有一个它独具魅力的地方.

作为一次非凡的学科间碰撞的结果，一个物理学的思路形成了，它把这个假设同粒子物理学的理论联系了起来.

当格拉姆的一串零点首次发表的时候，数学家们一定怀着强烈的敬畏来看待它，从传奇性的高斯时代以来就吸引了数学家们注意力的素数分布的秘密，如今以某种方式被锁在这一串数上，它们的实部都是，正如黎曼假设所确立的那样.

美国的数学家休·蒙哥马利（HughMontgomery）的研究比这更深入一步，他想知道的是，如果黎曼假设成立，即所有非平凡零点都分布在临界线上，那它们在临界线上的具体分布会是个什么样子？蒙哥马利提出了一个有关黎曼ζ函数的非平凡零点在临界线上的分布规律的重要命题（零点的对关联规律被称为“蒙哥马利对关联假设”），蒙哥马利与著名的英国物理学家戴森在普林斯顿研究所的一次偶然的邂逅，在数学与物理之间造就了一次奇异的交汇，黎曼假设也因此多了一道神奇瑰丽的景致.

当所有人把目光都聚焦在非平凡零点的实部的时候，蒙哥马利对ζ函数的非平凡零点之间的间隔（虚部）进行了研究，并发现这些间隔的分布函数具有的形式恰恰和物理学家戴森深入研究的量子动态系统联系在一起.

通过对ζ函数非平凡零点的大规模计算分析，一些数学与物理兼通的科学家发现这个临界线上的零点的分布有可能对应于某个量子力学体系的能级，非平凡零点的全体则对应于该量子力学体系的能谱.会不会有一天人们在宇宙的某个角落里发现一个奇特的物理体系，它的经典基本周期恰好是ln2，ln3，ln5，ln7……？或者它的量子能谱恰好包含14.1347251，21.0220396，25.0108575……？（还记得这些数吗？）也许并不存在这样的体系，但如果存在的话，它无疑是大自然最美丽的奇迹之一.只要想到像素数和黎曼ζ函数非平凡零点这样纯粹的数学元素竟有可能出现在物理的天空中，变成优美的轨道和绚丽的光谱线，我们就不能不惊叹于数学与物理的神奇，惊叹于大自然的无穷造化，而这一切，正是科学伟大魅力之所在.

蒙哥马利描述的临界线上ζ函数零点之间的距离给出了理论物理学家所谓的量子混沌系统中的能级之间的间隔，这种联系产生了两种可能：黎曼假设的证明可能在量子物理学中衍生出一些重大成果，或反过来，量子物理学的思想可用来证明黎曼假设.

法国数学家孔涅做出了一些卓有成效的研究，如果孔涅的方法有效，那将是数学与量子物理学之间联系的非凡例证，也将是第一次用量子物理学的方法解决纯数学问题.

当所有这些正在发生的时候，解析数学家们仍然不断地坚持他们的工作.他们延续着黎曼本人开创的传统，用复变函数论的工具来解决这个假设.其中重要的进展我们只能简单地罗列一下.

1912年，奥地利数学家阿廷在他的莱比锡大学哲学博士学位论文中运用域论，开辟了对黎曼假设的新的研究途径，成为黎曼假设研究中一个非常活跃的领域，其主要成果为：

有限域上代数曲线的黎曼假设：有限域上代数曲线的ζ函数的所有零点的实部都是.

黎曼的恩师狄利克雷是解析数论的领军人物，数学家把黎曼ζ函数推广，得到一个“豪华版”的黎曼假设，为纪念狄利克雷，推广的黎曼ζ函数叫作狄利克雷L函数：

广义黎曼假设：狄利克雷L函数的所有非平凡零点的实部都是.

变通后的黎曼ζ函数叫作戴德金ζ函数（戴德金，1831—1916，德国数学家，黎曼的挚友，黎曼传的撰稿人），戴德金ζ函数也是黎曼ζ函数的推广，第二款“豪华版”的黎曼假设叫扩展黎曼假设.

扩展黎曼假设：戴德金ζ函数的所有非平凡零点的实部都是.

狄利克雷L函数和戴德金ζ函数都是黎曼ζ函数的推广，都与普通黎曼ζ函数有着极大的相似性，数学家们发现，这些相似的函数都是一类被称为自守L函数的涵盖面更广泛的函数的特例，自守L函数是否也有相应的“豪华版”黎曼假设呢？答案是肯定的，这个史上最豪华的黎曼假设，它的名字也很气派，叫作“大黎曼假设”.

大黎曼假设：自守L函数的所有非平凡零点的实部都是.

对于我们高中生来说，上面的这些名称看了估计也跟没看一样，但我们毕竟看了.

证明或否证RH的前景如何，对这类事情发表预言，往往是不得要领的，即使是一个大数学家，这一点依然成立，希尔伯特曾预言证明黎曼假设的一个大概的时间，但失败了.

成立还是不成立？

最好的回答是：要么成立，要么不成立（终归可以判定，哥德尔的幽灵不会在这里出现）.

在相信它成立的大部分数学家中，完全是靠证据的分量来说话，所有的职业数学家都知道，证据的分量可能是一种很不可靠的测度.对于Li（x）总是大于π（x），证据的分量曾经很重，但是李特尔伍德1914年的成果否定了它.但对于黎曼假设，我们有多得多的证据，RH支撑着一大堆成果，它们大部分非常合理，并且用数学家们特别喜欢的一个词来说——“漂亮”.粗略的统计表明，在当今的数学文献中已经有数以百计的数学命题或“定理”以黎曼假设（或其推广的形式）的成立作为前提，黎曼假设通过那些命题或“定理”而与数学的许多分支建立了千丝万缕的联系，黎曼假设的命运与提出的这些命题或“定理”息息相关，一旦RH解决了，人类就站在一个不知比现在高多少的数学平台上，可看到更远得多的更美丽的风景.当然，如果RH不成立，它们全都面临崩溃.

在数学领域中，超过一个半世纪未能解决的猜想有很多，比如我们前面讲到的著名的费马猜想，自提出后隔了超过三个半世纪才被怀尔斯解决，迄今尚未被证明（或否定）的哥德巴赫猜想也已存在了两个半世纪以上，黎曼假设的历史与它们相比还差得远，但若以它们跟其他数学分支的联系，乃至与物理学那样的自然科学领域之间的关系（这些关系在很大程度上决定了一个数学猜想的重要性）而论，黎曼假设可以说是无与伦比的.

另一个衡量数学问题重要性的指标，是看看研究该问题的过程中是能否发展出新的有价值的数学手段，从这个角度上讲黎曼假设也是极为重要的，黎曼引入的复变函数方法使当时的数学中最大的问题“素数定理”得以证明，前面我们讲过的费马大定理的证明也在一定程度上受益于因研究黎曼假设而发展起来的一种叫“模算术”的代数几何手段.

已经越来越清楚，黎曼假设之所以成为数学中第一重要的问题，还在于它掌握着打开各种科学和数学研究之大门的钥匙，对黎曼假设的证明（不仅是这个结论，还有证明这个结论的方法）会产生素数模式的更多信息，这些信息不仅仅对数学而言十分重要，对于现代生活的许多重要领域的影响也是巨大的，比如网络安全.

每次银行使用自动取款机或在互联网上进行商业交易时，我们都依赖于素数的数学理论来确保交易安全.

当人们开始传递信息的那一刻起，下面的问题就产生了：如何防止截获这一信息的非授权人了解信息的内容，回答是对信息编码“加密”，如今，由于想成为密码破译者的人都能借助计算机的力量，设计安全加密系统极为困难.如果对加密文本有任何“可识别”的模式，用计算机进行精密的统计分析，密码通常可以解开，因此，你的加密系统需要足够牢靠，以抵抗得住计算机的攻击.

目前常用的RSA系统使用的解密密钥包含两个很大的素数（每个有100位），公开的加密密钥则是这两个素数的乘积，系统的安全性依赖于这样一个事实：至今还没有发现对大数快速进行因子分解的方法，也就是说实际上不可能从公开的加密密钥（两个素数的乘积）中得出解密密钥（两个素数），信息加密相当于求两个大素数的乘积（很容易得到），而解密相当于其逆运算因子分解（很难算出），当然，系统实际运作并非如此简单，其中还涉及一些其他相当难度的数学.

当今，一台强大的计算机在几天内所能分解的最大数大约只有90到100位，所以用两个100位素数的乘积，即一个200位的数作为密钥，会使RSA系统十分安全.但是，存在着这样的一种危险：数学家用来分解大数的方法不会像计算机那样机械，而是从理论上用一些高深莫测的方法寻找素因子.他们的方法巧妙而有效（如欧拉的641），这些方法运用了许多目前数学家们掌握了的素数知识，而当我们对素数的了解有进步时，总有可能导致因子分解出现新的方法.

由于黎曼假设告诉了我们如此多关于素数的信息，对这一猜想的证明很可能使因子分解方法有一个巨大的突破，而并不仅仅在于我们终于知道了这个假设是成立的.密码界所关心的是，证明这个假设成立的方法会对素数模式产生新的知识，从而发现更好的因子分解方法，依赖于素数特性的现代密码编制术和破译术，其根基就在于这个假设.

由于互联网安全问题迫在眉睫，极端重要，黎曼问题的含金量远比一百万美元的千年大奖要高得多.

希尔伯特有一次曾被人问到，如果他能在500年后重返人间，他最想问的问题是什么？希尔伯特回答说他最想问的就是是否已经有人解决了黎曼假设.

黎曼假设位于数学之巅，悬而未决，它或许比地球上任何真正的山峰更难征服，虽然攀登这座巅峰的艰难险阻被深深地笼罩在迷雾之中，但今天我们来到山脚下，向冷峻的巅峰投去深情的一瞥，无论怎样，懂与不懂，都是收获.我相信我们的努力是值得的，因为我们面对的是人类成就的顶峰.

最后，让我们重温1911年版《不列颠百科全书》中的“黎曼”词条，向伟大的黎曼告别：

他得以工作的年数不多，他的研究报告被印刷成页的也不多，但他的名字现在是，并且将继续是，一个在数学家中无人不知的词，他的学术成果大部分都是杰作——充满了独创性的方法，意义深刻的思想和广泛深远的影响.

——克里斯特尔