数论研究的前奏，来自《被遗忘的数学课》

对我们每个人来说，数学都是从算术开始的，算术研究的是最基本的数量概念，即整数1，2，3……谈到最普通的数学思想，区分个体数目的思想，那就是计数.

“上帝创造了整数，其他一切都是人制造的”，德国数学家克罗内克这句著名论述，揭示了整数内在的必然性以及它们无可否认的自然性，无论数学发展到什么阶段，整数总是根基.

数学家称这些无穷无尽的1，2，3……为正整数，或更形象地称它们为自然数.

算术一词不仅包含加减乘除这些基本运算，而且还包含整数的一些较深层次的性质，以前人们所说的高级算术实际上就是更难的算术的意思，今天更贴切的术语叫数论.

这门学科涉及的范围博大精深，它以素数概念为中心.如果一个整数比1大，而且不能写成更小的整数之积，那么这个整数就是素数.

公元前350年，欧几里得在其著名的《几何原本》中，用了很大的篇幅来讨论素数，特别是他证明了每一个大于1的计数数要么是素数，要么具有唯一的素数分解（次序变化不计），这个事实被称为算术基本定理.顾名思义，这个定理就是算术乃至整个数学中最基本、最重要的一个命题.

数的素数分解的唯一性要求我们把1从素数中排除，它既不是素数也不是合数，被称为单位.

素数的角色与化学元素的角色类似，就像关于一种物质的独特分子结构的知识能告诉我们该物质的很多特性一样，掌握了某个整数的唯一素数分解就能告诉我们这个整数的许多性质，素数被称为数的原子.

面对一个正整数，数学家首先希望确定它是素数还是合数，若它是合数，接下来就要寻找它的素数因子.有时候，这个问题很简单，如任意一个偶数（大于2）显然都不是素数，因为它有一个因子2，任何一个两位或两位以上的个位是5或0的整数也同样是合数，除此之外，确定素数性的问题就相对比较困难，比如谁能确定4294967297是素数还是合数？

高斯在其著名的《算术研究》中非常简洁地描述了这个问题：

“素数与合数的区分以及合数的素因子分解的问题是算术中最重要且最有用的问题之一……这门学科本身的高贵性要求人们应该探索每一个能解决这一充满奥妙的问题的方法.”从古希腊人到现代数论学家的2400多年间，数学家们义无反顾地扑向这一领域，就如同飞蛾扑火，前仆后继，沿途众多学者们创造了关于素数的很多猜测，其中有一些已经解决，但有相当数量的问题至今还没有得到解决，比如：对我们来说，最有名的是哥德巴赫猜想，20世纪60年代，陈景润的事迹曾深深地激励着我们一代又一代的青年学子.

陈景润（1933—1996）

哥德巴赫猜想最初出现于1742年一个数学迷克里斯蒂安·哥德巴赫（1690—1764）写给欧拉的一封信中，他在信中写到，任何一个大于4的偶数都可以表示成两个奇素数之和.欧拉经过研究，倾向于赞同哥德巴赫的猜想，但却苦于不知如何证明.

其后的两百多年的时间里，数学家们殚精竭虑，虽取得了不少的进展，但始终未能攻克这个猜想.

最接近这个猜想的研究成果是由我国数学家陈景润于1966年做出的，他证明了每一个充分大的偶数都可表示为一个素数和两个素数的乘积之和，简称“1+2”，媒体在宣传时通常称这个结论离最终的1+1仅一步之遥，但我们知道，这个“一步之遥”是最后也是最关键的一步，不知有多么遥远.

为了判定素数并造出素数表，公元前3世纪，古希腊数学家埃拉托塞尼提出了一个求素数的程序，比如，造出100以内的素数表，首先把1划去，保留2，然后划出所有2的倍数；3是素数，保留，然后划去所有3的倍数；5保留，然后划去所有5的倍数；以此类推，最后得到100以内的素数表：

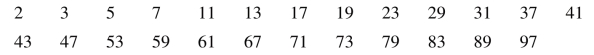
据说，当年埃拉托塞尼是用一种纸草紧固在木框上，纸草上写着数，凡是要划去的数就挖去，结果在纸草上密密麻麻留下许多洞，像筛子一样，“埃拉托塞尼筛法”由此得名.

显然，除2以外所有的素数都是奇数，但稍细观察一下就会发现，随着数值的增大，素数越来越稀少，这种现象不难做出解释，因为在我们观察比较小的数字（十几或二十几）时，由于小于这些数字的数很少，所以它们的可能的因子也很少，但对于比较大的数字（比如上万或上百万）来说，则有很多小于它们的数字可以充当潜在因子.一个数作为素数，必须没有更小的因子，一个大数很难做到这一点，因为它拥有许多小于自己的可能因子.

也许，远古的人们曾像今天的小学生一样，想到过素数可能会有尽头，素数越来越稀少，最后会完全消失不见，而后边的数字都成了合数.

欧几里得对素数的无穷性的证明，常常被人们作为数学定理的典范，因为欧几里得的证明简洁、优美，又极为深刻，英国数学家G.H.哈代在其精彩的《一个数学家的自辩》中曾深情地评价道：“……自发现之日至今，永葆其生机与活力，两千年岁月没有使它产生一丝陈旧感.”

定理：存在无穷多个素数.

证明：（反证法）假设只有有限多个素数，记为p1，p2，…，pn，它把全部素数都包含进来了，下面开始引出一个矛盾.

欧几里得构造了一个新的数N=p1p2…pn+1，它显然比p1，p2，…，pn中的任何一个素数都大，因为全部素数都在序列p1，p2，…，pn中，所以N一定是个合数，根据算术基本定理，N至少有一个素因子，它一定是序列p1，p2，…，pn中的某一个，到底是哪一个无关紧要，不妨设为pi，那么我们有N=pi·m，这样我们可得pi·m=p1p2…pi…pn+1，即pi（m-p1p2…pi-1pi+1…pn）=1，而这是不可能的.

当我们沿着这一证明返回去的时候，我们就会明白，前面的推理中唯一可能出问题的地方就是我们最初的那个假设有有限个素数上，因此，必须拒绝这个假设，这样，欧几里得通过反证法成功地证明了素数的数目必定是无穷的.

正因为数论中含有这些如此简单而美妙的结果，所以对于很多年轻人来说，算术是他们进入更高级数学的切入点，匈牙利数学家保罗·鄂尔多斯曾回忆说“当我10岁时，我的父亲给我讲了欧几里得关于素数无穷性的证明，从此我就上瘾了”.鄂尔多斯17岁时证明了任意两个整数n与2n之间一定存在素数，因为我们永远可以把数翻番，这也就给出了素数是无穷的另一种证明.

虽然人们把整数的唯一素数分解形象地比喻为化合物的唯一元素分解，但素数的无穷性使我们认识到，素数问题比元素问题复杂多了：历史上所有化学家的全部实验成果也不过是提供了区区100多种元素，虽说元素周期表也许能够挂满一面墙，然而素数表需要的则是一面可以无限延伸的墙.

人们曾有一个十分美妙的愿望：找出一个素数公式来，通过这个公式能得到全部的素数，从而能得到任意大的素数，但这一愿望一直未实现；人们又退而求其次，希望找出一个能生成部分素数的公式来——只要满足公式的数都是素数就行，而不必保证所有素数都可用此公式来表示.

又见欧拉，他给出了一个非常初级的多项式x2+x+41，这个式子的有趣之处在于当x取0，1，…，39时，x2+x+41可以连续取40个不同的素数值.

费马1640年提出一个猜想，称所有形如Fn=22n+1（n∈N）的数都是素数.

显然，F1=5，F2=17，F3=257，F4=65537都是素数，这也是费马做出这一猜想的依据，但F5=225+1=232+1=4294967297，这个数太大，当时的人们无法判断它的素数性，直至1732年，欧拉成功地分解了F5，从而否定了费马猜想.

欧拉设计了一个非常巧妙的检验方法，从一开始就排除掉所有无关的数字（欧拉像侦探一样，首先从一个线索的真正疑犯中排除无辜的旁观者），只留下几个潜在的因数，欧拉非凡的洞察力使拦在他面前的难题变得简单，这里的核心是欧拉得到了这样一个“线索”：

引理：若素数P能够整除232+1，则P一定为64k+1的形式：

当k=1时，P=65，不是素数；

当k=2时，P=129，不是素数；

当k=3时，P=193，是素数，但193不能被232+1整除；

当k=4时，P=257，是素数，但257不能被232+1整除；

当k=5时，P=321，不是素数；

当k=6时，P=385，不是素数；(www.chuimin.cn)

当k=7时，P=499，是素数，但499不能被232+1整除；

当k=8时，P=513，不是素数；

当k=9时，P=577，是素数，但577不能被232+1整除；

当欧拉计算k=10时，击中了要害，P=641是素数，且能整除232+1，

232+1=4294967297=641×6700417.

有趣的是，欧拉上述方法的依据正是费马发现的关于数论的一个结论“费马小定理”.费马搬起石头砸了自己的脚，更有意思的是从1640年起，数百年来的研究，人们发现，除了费马提出的最初的那几个费马素数外，再没有发现其他任何费马素数了，费马不仅错了，而且是大错特错，这也算是数学史上的一个奇观.

在涉及素数研究的问题中，其中最重要的一个问题是关于素数在整个整数中的分布问题，它们是以一种纯粹随机的方式穿插在整数中间吗？或者是它们以某种规律或者模式出现呢？大家都说“有些规律”，这显然是有些推诿和令人不满意的.

任何研究素数分布的人都是从这列表开始的：

表中列出了小于100的25个素数，如果这里存在某种模式的话，那么它一点也不明显，当然，2之后的所有素数都是奇数，但这显然没有什么太大的意义，人们注意到，这些素数中有几个缺口，如24到28以及90到96之间没有素数，分别是5个或7个合数，而与此同时，3和5，5和7，11和13，17和19，29和31，41和43以及59和61是背靠背的素数（孪生素数）.

增加数据量，我们收集第二个100中的所有素数，即从100到200：

这一次共有21个素数.我们又一次看到其中的缺口，例如从182到190之间有9个整齐的合数，而孪生素数对相对在减少.

在全面研究素数分布的过程中，缺口（在这之间素数相隔很远）和孪生素数（在这之间素数非常靠近）好像承担着重要的角色，素数之间有更长的缺口吗？孪生素数有无限多个吗？有趣的是，第一个问题很容易回答，而第二个问题是数论中至今都没有解决的问题之一.

连续合数（素数缺口的长度）可以这样产生：数11！+2，11！+3，11！+4，…，11！+10产生连续10个合数，501！+2，501！+3，…，501！+500可产生连续500个合数，从5000000！+2开始，利用完全相同的过程我们可以生成500万个连续的数，其中没有一个素数，同样，我们也很容易生成50亿个甚至5万亿个连续的合数，这样的推理产生一个惊人的结论：素数之间存在任意长的缺口.

5万亿个连续的整数中竟然没有一个素数，就在这一点，人们似乎可以肯定素数没有了，但欧几里得早就说了，在这些数的后面一定存在更多的素数，素数是无穷无尽的.

这样的状况太奇怪了.

有关素数模式的最深入的观察是由高斯率先提出的.

高斯对素数分布的研究始于1792年，那时他15岁，每当“无所事事”的时候，高斯就会挑上几个长度为一千的自然数区间，计算这些区间中的素数的个数，并进行比较.

我们来看一下百万以内的素数的密度.素数密度：小于N的素数的个数π（N）除以N，记为，（符号π（N）读作π-N，这里的π与3.1415926没有任何关系，希腊字母表中只有24个字母，而到数学家要给这个函数一个符号的时候，24个字母早已被用完，他们不得不开始循环使用它们，π（N）被定义为到N为止的素数的个数，包括N，但当要说“小于或等于”时，这种场合中数学家通常粗略地说“小于”）

显然，越往后，密度便越小，这样的减少一直持续，当然，数学家需要某种比诸如“随着我们向前走素数变得越来越稀少”这一类普通的观察更强大的东西，他们要寻找一个规律，或者数学公式，以此至少可以粗略地反映素数的分布.当高斯以一千的自然数区间计算这些区间中的素数到一百万的时候，发现素数的密度近似于一个函数；而这个函数也只有大师才能发现，它竟然是（自然之数e神秘地在这里现身），N越大，近似的程度就越好，通过取足够大的N，就能使密度DN与的接近程度达到人们所要求的任何精确度.

高斯发现素数的密度函数可用函数来描述，即（波纹号～的意思是“渐近地趋于”）.

这一结论可改写为.

这是一个非常重要的结果，它是如此的重要，以至于被称为“素数定理”！注意，不是“素数的一个定理”，而是“素数定理”，因为经常要引用，当上下文足够清楚的时候，数论专家通常简记为PNT.面上的含义是，对于充分大的N，能让我们省去逐个数的麻烦而得到直至N的素数的个数π（N）.（它还有两个推论，即N是素数的概率～1/lnN；另一个是第N个素数～NlnN，推论与定理等价，也是素数研究中两个极为重要的结论）.

如果想用图表现素数，最显然的方法是在x轴上的每一个素数处标一个点，显然它是一个离散的图（如图9-1（1））.

图9-1（1）

而函数lnx的图象是一条光滑连续的曲线.

为什么数轴上这些间距不规则的离散的点与坐标系中这条光滑连续的曲线有联系？函数lnx怎会告诉我们关于素数分布模式的事情呢？

lnx磨磨蹭蹭地增长，优美上升的曲线比x的任何幂都增长缓慢，不是比x2，x3缓慢，而是x0.1，x0.001之类，这是一件非常迷人、非常重要的事，给人以无限的想象空间.

图9-1（2）

素数定理告诉人们，尽管素数看上去是以随机的方式出现，但它们逐渐稀少的方式却遵循着一个系统的模式，如果你观察任何一段有限长的数，这样的模式未必明显，沿着数增大的方向，不论你走得多远，你总能发现有一些素数集聚在一起.同样，你也能发现在要多长就有多长的区间里，一个素数都没有.然而，当你收回目光，俯瞰整个计数数序列时，你会发现一个十分明显的模式，那就是N越大，DN越接近，当N越来越大时，素数就踏入了自然对数的节拍.

1777年，高斯出生于德国的不伦瑞克，1799年，因其对现在称之为“代数基本定理”的命题做出了第一个合理而完整的证明获得博士学位，2年后发表了他的数学名作《算术研究》，高斯继承欧拉的衣钵（欧拉逝世时，高斯刚刚6岁），成为世界上最优秀的数学家，他曾说过“数学，科学的皇后，数论，数学的皇后.”

高斯是一个平静、简朴而沉默寡言的人，淡泊名利，缺乏野心，追求完美.高斯对于他自己得出的任何成果，在推敲到洗练流畅、逻辑条理上无懈可击之前，是决不会公之于世的，他的个性标志表现为一棵只有稀疏果实的树，其格言是“虽然少，但却成熟”（PaucaSedmatura），高斯所发表的远远少于他所写的，但一旦下笔，就会引起数学界的注意，他身后的成果具备了任何数学著作所应具备的成熟.

1855年，高斯在德国哥廷根大学去世，他把他的事业传给了他曾指导过的博士生，也是他在哥廷根大学数学教席的第二任继承者：伯恩哈德·黎曼.

黎曼，正是我们今天讲座的主角.