被遗忘的数学课：微积分的奥秘与应用

在上一次的讲座中，我们回顾了积分和微分概念的产生和建立的过程，随着笛卡儿、费马解析几何的创立，我们可以把先辈们苦心得来的一些零星的发现，把形形色色的求积问题，统一归结到在坐标系平面内求曲线f（x）下的面积，从而建立了函数积分的概念；我们用平均速度逼近瞬时速度，用割线逼近切线，抽象出一种用平均变化率逼近瞬时变化率的方法，定义了函数的微分（导数）.但光有这些我们还无法真正了解微分和积分的奥秘和它们作为一个完整的算法系统所展现出的巨大的威力，今天的讲座我们将进入微分和积分的核心部分，建立微积分概念，掌握“微积分基本定理”.

我们还是从积分说起.

如今，随着生活水平的提高，人们的生活方式显得多样化，也越来越认识到运动健康的重要性，我和一帮“驴友”们经常外出开展户外登山活动，时常看到山上有“严禁吸烟”“山上炊烟、罚款三千”的警示牌，告诉爬山的人山上不能抽烟不能搞野炊玩火.有一次，我们发现一块警示牌上写着“一棵大树能造千万根火柴，一根火柴能毁千万颗大树”，大家驻足欣赏，有人说这句话有创意，比“严禁”“罚款”温馨、文明多了，让人记忆深刻；有人说这个警示牌有哲学意味，有意思，大家都点头赞许；我说了一句“这不就是微积分吗？”语出惊人，可惜无人喝彩.

山上有各种各样的树木，我生长在农村，读书时也不像现在的这般光景，我们漫山遍野地跑，山上的野果吃尽了，认识的树种也多，有杨树、株树、枞树、楮树、檵树等等，现在的学生就可怜了，可能只认得樟树、梧桐树了.山上这么多树，大小不一，形状各异，如何来度量它的体积呢？这个警示牌告诉我们，我们可以把各种各样的树，管它粗也好，细也好，直也好，弯也好，若通过某种方法，全部制作成火柴，那么，这棵树可制成a根火柴，那棵树可制成b根火柴，另一棵歪脖子树可制成c根火柴，这不就把它们得体积都度量出来了吗？

言归正传，积分思想中的“分割-求和”方法，它需要两个技巧，一个是分割的技巧，如阿基米德采取特殊的形式用三角形去铺满抛物线弓形，费马用特殊的分割求曲线y=xn下的面积，而开普勒的酒桶里面就藏有更多这方面的技巧，虽然我们现在一般采用在坐标系下用等宽的“矩形”来分割，通过把矩形的宽无限缩小，最后使矩形变成线段，由线织成布，基本上解决了分割的问题，但我们还将面临如何代数求和的问题，有些求和比较好解决，有些求和会比较困难，甚至解决不了，所以这种方法的成功与否取决于几何技巧和代数技巧，有时还要看是否能得到幸运女神的眷顾.

能否找到一种新的途径来解决问题呢？

问题：如图8-3（1），求y=sinx在[0，π]上的投影面积.

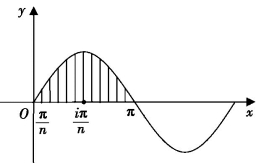
图8-3（1）

按定积分的定义，我们把区间[0，π]n等分，分点坐标分别为对应的高分别为右端点的高表示为则面积为

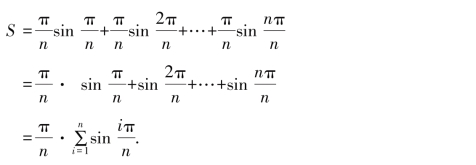
用莱布尼茨的表示法即为定积分

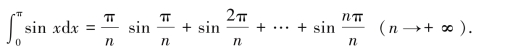
对于这个求和，我们还算幸运，这个求和还难不倒我们优秀的高中生：

令，利用公式（*）可得：

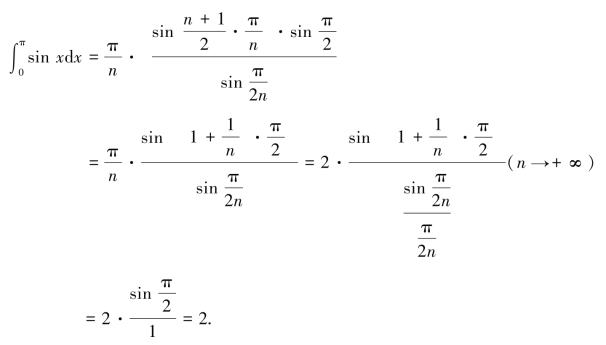
解法2：根据牛顿给出的积分的三个法则，我们首先把sinx用幂级数展开：

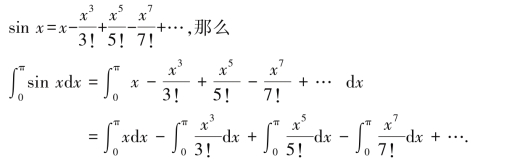
注意，这一步有危险.因为在牛顿法则2中，论述的是有限项的和的积分等于有限项的积分的和，而这里我们面对的是一个无限项的和.让我们学学欧拉吧（欧拉经常做这样的事情，欧拉有敏锐的数学直觉，他知道哪里可以向前推进，哪里不能乱来），看看是否有好运气.

因为有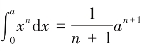，所以每一项的积分都容易求得：

对于这样一个头疼的求和，我们大概就无能为力了.

17世纪，很多数学家对由“无穷小量”建立起来的一套积分方法和微分方法做了大量的开创性工作，积分和微分都差不多形成了各自的体系，但这两个体系一直是两个孤立的系统，只有两个人洞察一切，深谙其中的奥妙：我们碰到的积分求和问题，其实与微分有关.

卡瓦列里的《不可分量几何学》是研究几何中无穷小问题的数学家用得最多的著作，卡瓦列里曾经用几何术语阐明了一个等同于的定理（其中n为所有正整数），这也许应该被看作积分的第一个普遍性定理，它也出现在帕斯卡等人的著作里，而我们在前面已经回顾了费马用特殊的分割法对这个结论的证明，事实上，费马在这方面领先于所有其他人.

费马在研究曲线的切线时，也得到了曲线xn在x点的切线的斜率为nxn-1，然而，奇怪的是，他为求积和求切线研究出了卓越的运算方法，居然没有发现求和和切线问题间的联系，作为解析几何的创始人之一，错过确实可惜.

费马未能将自己的方法加以提炼、推广和一般化，他可能把自己的这些研究仅仅当作对一些具体问题的解答，而没有意识到它们的深远意义.可能还没有别的数学家像费马那样，如此接近于发明微积分.

事实上，情况是这样的：

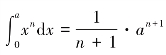也就是，这是积分；

而（xn）′=nxn-1，也就是（xn+1）′=（n+1）xn，即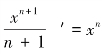，这是微分.

我们从两个不同的系统得到两个结果，把它放在一起：

.

这提示人们，微分与积分是相互包含的一种互逆运算.

牛顿是从运动学方面捕捉到微积分的.1671年，牛顿在《流数法和无穷级数》论著中，用清晰准确的语言阐述了微积分的两个基本问题：一是已知流量间的关系求流数的关系，这就是已知函数f（x），求它的导函数F（x）F（x）=f′（x）；另一个是已知表示量的流数的关系求流量的关系，也就是已知F（x）=f′（x）求f（x）f（x）=∫F（x）dx，并指出这是两个互逆的问题.

由此，牛顿把这两类问题联系起来考虑，并做出了一个重大的发现：他发现微分学和积分学通过一个定理，密切而互反地联系在一起，这个定理就是今天的“微积分基本定理”.

在牛顿之前，伽利略在处理匀加速运动时，证明了在V—t曲线下的面积就是距离，这个结论使他的学生托里拆利也认识到，变化率的问题本质上是面积的逆问题.

问题：在V-t坐标下，求时间间隔[a，b]内运动物体的距离.

我们把[a，b]分成n个区间，在每一个微小区间（Δt=ti+1-ti）内的平均速度可用端点的瞬时速度来替代，这样运动物体所走的路程就是：

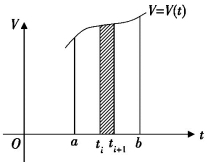
图8-3（2）

，而这个和就是如图所示的所有小矩形的面积和，这正是函数V（t）在[a，b]上的定积分.设路程与时间的函数关系为S（t），则运动物体在[a，b]时间内所走的路程可表示为S（b）-S（a），故我们有

另一方面，在S=S（t），t∈[a，b]的函数关系中，代表的是时刻t的瞬时速度，也就是函数S（t）的导数S′（t），即速度是路程对时间的导数

(www.chuimin.cn)

将（2）代入（1）式可得，

这样我们就有：若S′（t）=V（t），那么.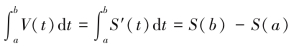

把这个结论一般化，我们得到一个重要的公式：

若F′（x）=f（x），那么，函数F（x）叫作函数f（x）的原函数.这个公式就是微积分基本定理，史称牛顿-莱布尼茨公式.

现在，再让我们回过头去看前面的例子：求，我们可以这样解：

因为（-cosx）′=sinx，

所以

=-（cosπ-cos0）

=2.

这太爽了，我们再也不用去苦思冥想如何分割，怎样求和了.

相对于牛顿从运动学方面捕捉微积分，莱布尼茨的考察方式更侧重于数学和哲学，莱布尼茨观察到求曲线的切线依赖于纵坐标与横坐标的差值的比值（当这些差值变成无穷小时），莱布尼茨把它表示为微商或差商的形式（dx→0），而求面积则依赖于在横坐标的无穷小区间上无限窄矩形面积之和，莱布尼茨将它表示为∫ydx，先进的符号表示也便于帮助莱布尼茨丢弃枝叶而思考微分和积分之间的本质联系.

如图8-3（3）所示，设区域K的面积为S，记为.我们在x轴的区间[a，b]内取点P（x，0）（如图8-3（4）），通过这个点且垂直于x轴的直线与曲线交于Q，则Q的坐标为x，f（x），记区域K内直线x=a和线段PQ所夹的部分的面积为S（x），则面积函数S（x）是x的函数，我们给x一个微小的增量Δx，点P移动到P′的位置，P′的坐标为P′（x+Δx，0），相应的Q′的坐标为x+Δx，f（x+Δx），此时面积增量

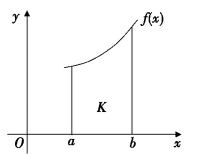
图8-3（3）

图8-3（4）

另一方面，由P的微小变化引起的面积的增量即图中的阴影部分，这个图形的左边界是线段PQ，它的长度为f（x），而右边界是线段P′Q′，它的长度是f（x+Δx），当Δx无限小时，两者可视为长度相同.我们将面积增量看成长方形.它的面积是

由（1）（2）可得S（x+Δx）-S（x）=f（x）·Δx（Δx→0），

将两边同时除以，

也就是S′（x）=f（x）.

这表明，面积函数S（x）的导函数是f（x），即面积函数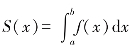有一个导数，它恰好是同一个函数f（x），我们把S（x）叫作f（x）的原函数.设f（x）的原函数之一为F（x），则有

S（x）=F（x）+C.

当x=a时，显然S（a）=0，所以C=-F（a）.

由此，面积函数S（x）=F（x）-F（a）.故此，当x=b时，所求的面积为S=S（b）=F（b）-F（a）.

综上所述，我们得到：若F（x）为f（x）的原函数，则有

积分可以追溯到古希腊的阿基米德所建立的确定面积和体积的方法，而微分起源于作曲线的切线和计算变量的变化率的问题.在16世纪末17世纪初，开普勒、费马、沃利斯和巴罗都研究过这些问题，但是他们都没有发现积分和微分的互逆关系，以形成系统的理论和创建一种普遍适用的方法，这时需要有一种人来完成这最高和最后的创造性工作.这种人要能敏锐地从纷乱的猜测和说明中清理出前人有价值的想法，要有足够的想象把这些碎片重新组织起来，而这正是牛顿和莱布尼茨联合贡献的.

至此，微积分的概念对我们不再是“从天而降”，这有助于我们进一步理解微分和积分概念的本质和把握它们之间的关系.“微积分基本定理”也不再是稀里糊涂地轻松捡来，我们再用牛顿-莱布尼茨公式解题时也会显得底气十足.

让我们回想一下电视播放的动画片，制作者画的一幅一幅的画当然是不会动的（其实是一张张图片），每幅图片上画的都会有一点点微小的变化，但当制作者以每秒几十枚图片的速度播放这些图片时，整体看上去，那“画”就自然连贯动起来了.

连续两张图片上描绘，后一张比起前一张只是在动作上有了非常微小的变化（换一句话说，图片是以微小的时间幅度将连续动作切分，一个一个画面进行描绘），我们观察动作中微小变化就是所谓的“微分”，而连接一系列微小变化，使整体顺当地活动起来就是所谓的“积分”.

“变化和合并”，即感知非常细小的变化和趋向，从而从整体上把握这一变化，正是微积分最擅长的领域.

在这个日益多样化的信息社会，我们置身于各种各样的变化之中，我们需要捕捉这些变化，并综合地理解和把握全局，因此有必要掌握微积分的思考方式和相关知识.

莱布尼茨在1684年的一篇论文中率先发表了他的研究成果，文章的标题中包含了一个拉丁词Calculi（意指一种计算系统），这个词后来就用来指代这门新生的数学分支，第一本微积分教科书在十几年之后面世，微积分（theCalculus）的名称在书中被确定下来.

莱布尼茨是伟大的符号发明者，他用积分符号“∫”取代求和∑，用微商取代差商.导数这个符号有很大的优越性，例如对y=f（x）的反函数x=g（y），其微分法则是f′（x）·g′（y）=1，按照莱布尼茨的记号，它简单地记作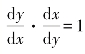，如同“微分”可以像普通分数约分似的，而对复合函数Z=gf（x）Z=g（y），y=f（x）的微分法可表示为.

莱布尼茨的符号特别强调了算法的特点，在微积分理论中是不可缺少的.只是这种记号太优越，正好导致了我们的微积分学习也成了空洞的符号游戏式的解题训练，而没有对微积分概念的透彻理解和准确把握，这正是我们平常教学的重大失误之所在.

如果说牛顿、莱布尼茨是微积分的奠基者，他们作为卓越的建筑设计师，为我们设计了一幅宏伟的蓝图，但是这份蓝图终究需要一支建筑队伍来将其变成一座大厦.正是伯努利兄弟等人所做的大量工作，才把微积分建立成今天我们所知的这门学科，他们进行系统的阐述，充实它的细节，研究、完善了统一性、条理性和相关术语（“积分”一词正是雅各布·伯努利给出的），在他们手中，微积分变成了当今学生易于接受的形式：即具有基本的概念，求导法则、积分方法和初等微分方程的解法.世界上第一本微积分教科书正是由约翰·伯努利完成的.

像之前的牛顿和莱布尼茨以及许多后来的数学家一样，雅各布·伯努利认为无穷级数是进入分析学的必由之路.而约翰·伯努利在18世纪20年代，培养了一名前途无量的年轻的瑞士学生，这位学生的名字正是莱昂纳德·欧拉.

欧拉用三部著作《无穷小分析引论》《微分学原理》和《积分学原理》赢得了“分析的化身”的崇高地位，随着伯努利兄弟、欧拉、黎曼等人的努力，微积分迅速上升发展成为一门新的学科——分析学（数学分析），极大地推动了数学和其他自然科学的蓬勃发展.

拉格朗日进一步扩大了分析学的领域，通过他的一部被誉为“科学诗篇”的《分析力学》，把力学变成了分析学的一个新分支.黎曼更是强调“只有在微积分发明之后，物理学才成为一门科学”.

欧拉于1783年辞世，这一年距离莱布尼茨发表第一篇微积分论文一百周年仅差一年，无论按什么标准衡量，这一百年都是数学史上非同寻常的一个世纪，在经历了微积分学的狂飙突进之后，人们终于冷静地回过头来审视微积分的逻辑基础了.

微积分能行之有效的确切原因，自微积分创立以来就一直使数学家们迷惑不解，然而人们利用微积分能够做出这么多惊人的事情，埋怨它缺乏严格的数学基础似乎是有些大题小做，因此，在很长的时间里，微积分的先驱们多半依靠直觉而不是根据逻辑推理进行运算.不可否认，他们的直觉通常是非常可靠的.特别是欧拉，他具有一种神奇的能力，在他陷入数学的深渊之前就能准确地知道自己可以走多远，然而再强的直觉也存在着陷阱，微积分的根基所依赖的逻辑原理再也不能简单地忽视下去了.