所有科学的发展都以一条假设为基础:宇宙在以一种可以为人类所理解的方式运转.在纷繁多彩、令人诱惑的自然现象背后,隐藏着某种简洁的规律,人类思维能与这种规律协调相符,多亏有了数学,人类正是通过数学来研究探索宇宙运行的基本法则.数学是科学发展的基石.在许多同学们的眼里,阿基米德、牛顿是以物理学家的形象出现的,殊不知他们还是最杰出的数学家.今天我向大家再重点介绍一个人物,他也是一位物理学家,但他同时也应该......
2023-11-19
“微分”,“微”是“细微、微小”的意思,而“分”的意义是“细分、分割”,微分,就是通过观察事物微小变化或瞬间特征来把握事物整体的一种方法.
积分的萌芽和产生可以追溯到久远的年代,起源于面积的计算(而后扩展到体积和弧长),在运动、变量进入数学之前,积分实际上是一种静态的、孤立的计算技巧(这个技巧就是前面我们讲的分割求和的方法),而微分的兴起则是17世纪以后的事情.随着欧洲文艺复兴运动的蓬勃发展,物理学、数学、天文学都取得了突飞猛进的发展,微分的概念应运而生.
我们先从运动学入手.
我们知道,自然界物体的静止是相对的,而运动是绝对的,换一句话说,运动物体的匀速运动是一种特殊的状态,变速运动才是常态.如何来把握、刻画变速运动物体的运动状态呢?最常见的一个量就是速度.根据定义,速度是运动物体的位移与时间的一个比值,这里的时间指的是一个时间间隔(区间),速度刻画了在这个时间间隔内物体位移变化的快慢,这个速度实际上是一个平均速度,也就是运动物体位移的平均变化率,如图8-2(1),某人徒步旅行去登山,从起点A出发,经过平缓的上坡,陡峭的上坡和平缓的下坡到达山脚下D,假设全部路程是18km,除去休息时间共用6h,那么全程的平均速度为18÷6=3km/h,如果我们觉得用这个全程的平均速度来刻画登山者的运动状态过于粗糙,那么我们还可以分别求出AB,BC,CD三个阶段的平均速度,这样就相对准确地描述了登山者的运动状态了,当然最能准确把握登山运动状态的一种情形是描绘出登山者在整个登山过程中任一时刻(图中任意一点,如P点)的速度,这就是所谓的“瞬时速度”.

图8-2(1)
全部路程18km,所需时间7h(含休息时间)
牛顿显然是这方面的大师,我们来看看牛顿是如何解决关于瞬时速度这一问题的.
问题:计算小球自由下落第10秒的瞬时速度.
速度等于位移除以时间,用小球10秒内自由下落的位移除以10,得到的是小球自下落起10秒内的平均速度.因为小球下落是变速运动(速度会越来越快),这个平均速度显然不能作为第10秒的瞬时速度,但若直接计算,第10秒代表的时刻是指时间间隔为0的一个瞬间,此时小球下落的距离也是0,结果就是0除以0,这等于没有结果,当然,这难不倒牛顿.
牛顿考虑用小球下落第10秒后的一段时间间隔来代替第10秒这一时刻,用它在这一段时间间隔内下落的距离除以这个时间间隔,就得到在这一时间间隔内小球的平均速度,当这个时间间隔越短,计算出来的平均速度就越来越逼近第10秒这个瞬间的瞬时速度.
小球的运动状态可用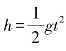 来描述,牛顿给第10秒一个时间增量Δt,那么小球在这个时间间隔[10,10+Δt]内的平均速度为
来描述,牛顿给第10秒一个时间增量Δt,那么小球在这个时间间隔[10,10+Δt]内的平均速度为
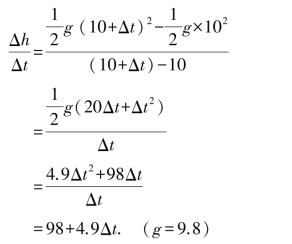
最后牛顿让时间间隔Δt无穷小,令Δt=0,得到小球第10秒的瞬时速度为98m/s.
牛顿给时刻t一个时间增量Δt,就能算出在时间间隔[t,t+Δt]内小球的平均速度(也就是小球在这个时间间隔内位移的平均变化率),然后通过减小这个时间增量Δt,使其成为“无穷小”,这样,平均速度就无限逼近时刻t的瞬时速度(瞬时变化率).
我们把牛顿的方法一般化,在某个变化过程中,变量的关系用函数y=f(x)来表示,在自变量x从x0变化到x1的过程中,自变量的增量用Δx来表示,Δx=x1-x0,此时函数值的增量为Δy=f(x1)-f(x0),那么函数的平均变化率为![]()
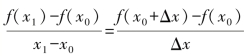 ,当自变量的增量Δx趋近于0时,这个平均变化率就趋近于函数在x0点的瞬时变化率.
,当自变量的增量Δx趋近于0时,这个平均变化率就趋近于函数在x0点的瞬时变化率.
当牛顿用平均变化率向瞬时变化率逼近时,其他的数学家也在考虑另一条通向微分的道路,即研究运动曲线的切线.
我们在看赛车的时候,有时会看到赛车由于速度过猛而来不及拐弯,车子会沿着这个弯道曲线的切线方向飞出赛道,这时,脱离赛道方向的直线和这个赛道只有一个公共点,这个点就是“切点”(如图8-2(2)),同样在链球比赛场地,当选手把链球做回旋运动加速,在链球离开手的瞬间,链球并不是从中心笔直向外飞出去的,而是向着圆的切线方向飞,如图8-2(3).
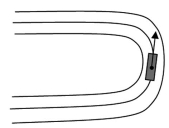
图8-2(2)

图8-2(3)
从上面的例子我们可以看出,切线决定运动物体瞬间的运动方向,而所有运动方向的合成就构成运动曲线本身,如图8-2(4).
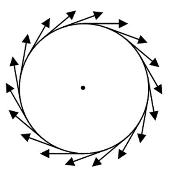
图8-2(4)
那么,如何用一个量来画切线的方向呢?我们知道,这个量就是曲线切线的斜率.
我们想象一下起伏的山峦,每座山都有山顶和谷底,山的倾斜也时急时缓,山顶、谷底、缓坡、陡坡就是构成山峦的要素,而沿着“山峦=曲线”的思路思考时,这些就成为曲线的基本要素.如图8-2(5),当曲线缓缓上升时,切线的倾斜也是平缓的(斜率的绝对值小),取正值,当曲线突然上升时,切线的倾斜也大(斜率的绝对值大),取正值,相反,当曲线下降时,切线的斜率取负值,而在山顶部分,切线是平的,切线的斜率值为0(谷底部分也一样),决定曲线上各点的切线的斜率对于把握曲线的特征而言是关键.

图8-2(5)
如何求曲线切线的斜率呢?我们还是从熟悉的地方入手.
问题1:如图8-2(6),求过圆M:(x-2)2+(y-3)2=2上一点P(1,2)的切线的斜率.
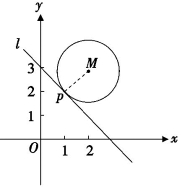
图8-2(6)
圆是最常见的曲线,关于圆的切线我们有“切线与过切点的半径垂直”可利用,点M,P的坐标分别为M(2,3),P(1,2),故直线PM的斜率![]() =1,切线l的斜率是直线PM的斜率的负倒数,所以kl=-1.
=1,切线l的斜率是直线PM的斜率的负倒数,所以kl=-1.
问题2:如图8-2(7),求抛物线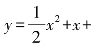
![]() 上点P(1,3)的切线的斜率.
上点P(1,3)的切线的斜率.
我们没有了问题1中的圆的特殊的性质可用,根据切线的特征,切线与抛物线只有一个交点,我们把切线与抛物线方程联立,利用一元二次方程Δ=0来解决.设切线的方程为y-3=k(x-1),联立方程组:
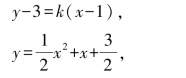

图8-2(7)
消去y,化简为x2+(2-2k)x+2k-3=0.
令Δ=0,即(2-2k)2-4(2k-3)=0,解得k=2.
其实,对一般的二次曲线,我们都可以用此类方法求得切线的斜率,但对其他的曲线诸如![]() ,人们需要考虑一个一般的方法.(www.chuimin.cn)
,人们需要考虑一个一般的方法.(www.chuimin.cn)
仍以问题2为例,如图8-2(8)所示,我们给点P(1,3)的横坐标x=1的一个增量Δx,相应地点P的纵坐标的增量为Δy,则横坐标为1+Δx对应的点Q的纵坐标为3+Δy,连接PQ,直线PQ为抛物线的一条割线.
问题的关键是我们让点Q动起来,当Q点从P点向上移动时,Δx从(1,0)向右増大,此时割线PQ的斜率会越来越偏离切线的斜率,当点Q在P点上方向下运动时,Δx向左逐步向(1,0)靠近,此时,割线会逐步与切线靠拢,以致无限接近切线.当Δx→0时,我们说割线将与切线重合,我们用割线PQ的斜率来逼近切线的斜率,用代数语言来反映这个过程就是:
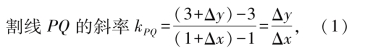
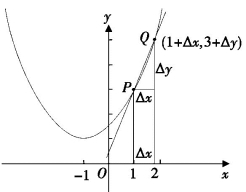
图8-2(8)
显然Q(1+Δx,3+Δy)在曲线上,代入曲线方程,我们有

这就是过点P的切线的斜率.
这个方法的重要意义在于它适合于一般的曲线,我们把它一般化:
如图8-2(9),对于曲线(函数)y=f(x),A点的坐标A(x0,y0),对于自变量x0的一个增量Δx,B点的坐标记为x0+Δx,f(x0+Δx),比值![]() 当Δx→0时的极限值就是过A点的曲线切线的斜率,它描述了曲线在A点的运动方向.
当Δx→0时的极限值就是过A点的曲线切线的斜率,它描述了曲线在A点的运动方向.
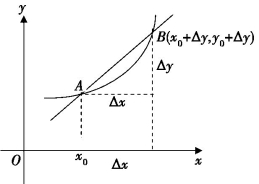
图8-2(9)
罗素说:“不知经历了多少年,人类才发现一对锦鸡和两天同是数字‘2’的例子.”数学家最擅长的就是从具体的事物中抽象出本质来,形成概念.数学家们发现,用平均速度来逼近瞬时速度,用割线的斜率来逼近切线的斜率,用事物的平均变化率来逼近瞬时变化率,都是“2”的例子.
定义:对于函数y=f(x)中的一点(x0,y0),给自变量x0的一个增量Δx,若极限值 存在,我们就把这个极限值叫作函数f(x)在点x0的导数,记作f′(x0).
存在,我们就把这个极限值叫作函数f(x)在点x0的导数,记作f′(x0).
这就是微分(导数)的定义.
x0取遍函数f(x)定义域中任意一个值,如果导数都存在,就用变量x取代x0,极限值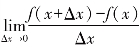 仍是一个x的函数,我们把它叫作f(x)的导函数,用f′(x)表示.
仍是一个x的函数,我们把它叫作f(x)的导函数,用f′(x)表示.
牛顿从运动的角度考虑,把变动的量(如无穷小的时间增量Δt)叫作流动的量,简称“流量”,把利用无穷小流量计算出的瞬时速度叫作“流数”,在牛顿的体系中,无穷小增量Δx用“0”(瞬)表示,导函数f′(x)用f·表示.
莱布尼茨用dx表示Δx,dy表示Δy,在莱布尼茨体系中,f(x)的微分(导数)表示为![]() .
.
费马对确定函数f(x)的极大与极小的问题很感兴趣,我们知道,在函数的图象中,极大对应一个峰顶,它比相邻的其他点都高,而极小对应谷底,它比相邻的其他点都低.为了刻画极大点和极小点的特征,最好的方法是用曲线的切线,因为曲线在每一点的方向都由切线给出,在极大点和极小点,曲线的切线必须平行于x轴,如图8-2(10),f′(x)>0表示该曲线上升,负的导数f′(x)<0就表示曲线下降,而f′(x)=0就表示曲线在峰顶或谷底,切线处于水平方向,斜率必然是零,因此,对于f(x),解方程f′(x)=0就可以找到极大和极小的位置,我们津津乐道的“一阶导数等于0”正是费马首先提出的方法.
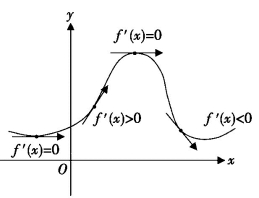
图8-2(10)
微分的概念虽然和函数图象相联系,但是导数(微分)概念的意义绝不仅仅是求曲线切线的斜率的问题.自然科学中,微分常用来计算随时间t变化而变化的某个量f(t)的变化率,而这也不仅仅是牛顿的瞬时速度问题,它包含自然界的无数的变化现象.
经过牛顿和莱布尼茨以及他们的后继者的工作,这些处理个别问题的技巧,逐渐形成了一个有效的一般的方法,只要掌握了少数几条简单的法则(如和、差、积、商、反函数、复合函数的求导法则),就可用这些方法毫不费力地微分数学中出现的各种函数,这样,微分法就有了计算中“算法”的特性.
我们不打算在这里详尽地阐述这套方法,举个例子说明一下:
例:求f(x)=xn的导函数.
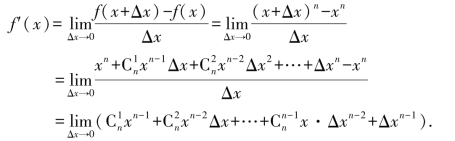
当Δx→0时,除第一项外其他项都是0,故(xn)′=nxn-1.
当历史的进程迈入18世纪,欧拉在微积分的世界里如鱼得水.1755年欧拉在其《微分学原理》一书中,给出了微分学的一些常见的公式,这些公式建立在“无穷小量”概念的基础上.在欧拉看来,微分dx就是0,因此表达式x和x+dx是相等的,并且在必要时可以互换.“同有限量相比,无穷小量消失为零,因此可以忽略不计”,此外,像(dx)2和(dx)3比dx还要小,所以同样可以随意丢弃.
欧拉通常需要寻求的是微分之比,并且确定这个比值,这相当于对![]() 赋予一个值,而这正是微分的使命.
赋予一个值,而这正是微分的使命.
例:(欧拉的一个微分)求y=sinx的微分.
欧拉从牛顿级数开始:
![]()
用微分dx代换x有:
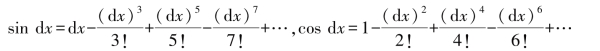
这两个级数化简为
sindx=dx,cosdx=1.
对于y=sinx欧拉用y+dy代替y,x+dx代替x,即有
y+dy=sin(x+dx)
=sinxcosdx+cosxsindx
=sinx+cosxdx.
即dy=cosxdx,由此推出两个微分的比值![]() ,即(sinx)′=cosx.相对于我们用定义来算,欧拉的方法有些意思.
,即(sinx)′=cosx.相对于我们用定义来算,欧拉的方法有些意思.
有关被遗忘的数学课的文章

所有科学的发展都以一条假设为基础:宇宙在以一种可以为人类所理解的方式运转.在纷繁多彩、令人诱惑的自然现象背后,隐藏着某种简洁的规律,人类思维能与这种规律协调相符,多亏有了数学,人类正是通过数学来研究探索宇宙运行的基本法则.数学是科学发展的基石.在许多同学们的眼里,阿基米德、牛顿是以物理学家的形象出现的,殊不知他们还是最杰出的数学家.今天我向大家再重点介绍一个人物,他也是一位物理学家,但他同时也应该......
2023-11-19

在上一次的讲座中,我们回顾了积分和微分概念的产生和建立的过程,随着笛卡儿、费马解析几何的创立,我们可以把先辈们苦心得来的一些零星的发现,把形形色色的求积问题,统一归结到在坐标系平面内求曲线f(x)下的面积,从而建立了函数积分的概念;我们用平均速度逼近瞬时速度,用割线逼近切线,抽象出一种用平均变化率逼近瞬时变化率的方法,定义了函数的微分(导数).但光有这些我们还无法真正了解微分和积分的奥秘和它们作为......
2023-11-19

那就是数学的圣地:微积分.微积分的发明是现代数学取得的最高成就,对它的重要性怎么估计也不过分.恩格斯甚至声称:“在一切理论成就中,未必有什么像17世纪下半叶微积分的发明那样被看成人类精神的最高胜利了.”对于数学中的这个“王者”,我们同学们都了解多少呢?微积分从萌芽、创建到完善,经历了两千多年曲折的过程,对这部宏伟画卷所展示出的非凡的魅力,我们又有多少人体会到了?......
2023-11-19

前几年浙江卫视《一周立波秀》节目作为中国的脱口秀名噪一时,很受欢迎,其中有一期节目谈到学校教育.我们小学数学的很多应用题中的主人公都叫小明,什么抽水问题、相遇问题、盐酸和水倒来倒去的问题,很是头疼,把小明都要弄成神经衰弱了,不知可怜的小明现在怎么样了,等到我们读初中,知道那些问题都可用方程来解,似乎一下子可控制住了,初中老师经常会说“世界上的任何问题都是数学问题,任何数学问题都是方程问题”,以此来......
2023-11-19

哈代在其著名的《一个数学家的辩白》中写道:“年轻人应该证明定理,而老年人则应该写书,任何数学家都永远不要忘记:数学,较之别的艺术或科学,更是年轻人的游戏,举一个简单的例子,在英国皇家学会会员中,数学家的平均当选年龄是最低的.”数学很大程度上是年轻人的科目,它是智力的竞争,只有年轻和才气旺盛才能充分满足它的要求,同昔日的体坛英雄一样,许多才华横溢的年轻数学家,在写出一两篇有前途的论文后便湮没于世.拉......
2023-11-19

对我们每个人来说,数学都是从算术开始的,算术研究的是最基本的数量概念,即整数1,2,3……谈到最普通的数学思想,区分个体数目的思想,那就是计数.“上帝创造了整数,其他一切都是人制造的”,德国数学家克罗内克这句著名论述,揭示了整数内在的必然性以及它们无可否认的自然性,无论数学发展到什么阶段,整数总是根基.数学家称这些无穷无尽的1,2,3……......
2023-11-19

为帮助青年教师成长,数学组开展“结对子”活动,我算是属于“经验丰富”之列,青年教师A跟我学,拜我为师.高一数学新增了向量内容,A要求听一堂课,按教学计划下一堂课应该是《向量的数量积的坐标表示》,我认真做了准备,新课将由常规的“复习式”引入.“同学们,关于向量的运算,我们从几何上定义了向量的加法和减法,研究了向量加法和减法的运算律,然后通过向量的坐标表示,用数量运算取代向量加减的几何运算.前几节课我......
2023-11-19

对某一学科或某一事物,人们常常用“分类”思想来进行把握和认识,仅仅就解题而言,我们知道“分类讨论”通常也是一种重要的解题手段,对我们普通的中学生而言,数学是什么?......
2023-11-19
相关推荐